基于灰熵法的沥青混合料低温抗裂性能影响因素研究

侯 伟

(重庆交通大学，重庆400074)

沥青混合料是一种典型的弹、黏、塑性体，具有很强的感温性［1］。在寒区或温差较大地区，当沥青路面所受温度应力超过沥青混合料的极限抗拉强度时，就会产生裂缝。在我国北方地区，低温开裂是沥青路面的主要病害，严重影响了沥青路面的使用质量和寿命。为减少或消除低温缩裂，提高路面品质，深入开展沥青混合料抗裂性能的研究显得非常必要。

沥青路面低温开裂是多因素共同作用的结果，可分为外因和内因。外因主要是气候环境因素，与气温和降温速率有关;内因主要包括沥青和石料性质、沥青混合料组成、沥青膜厚度和路面结构等［2］。在外因难以控制的情况下，综合考虑原材料的性质和组成，结合当地的气候环境特征，通过合理的沥青混合料设计来改善沥青路面的低温抗裂性能是积极可行的途径。基于沥青混合料低温抗裂性能是一个典型的“灰色系统”，笔者选用灰关联熵分析法进行系统分析，从而筛选出影响混合料低温抗裂性能的较为显著的因素，为后续工作奠下基础。

1 灰关联熵分析法

灰色理论是邓聚龙教授于1982年3月提出的一种新型工程系统理论［3］。该理论发展了一系列灰色系统的综合分析方法，其中包括灰色关联分析法。灰色关联分析法能在“小样本、贫信息”的条件下对系统进行分析，从而找出各种因素与系统发展态势之间的关系，并对系统的发展作出积极有效的引导，因此具有很强的实用性［4］。由于现有的灰色关联方法存在以下缺点:①局部关联倾向，即在点关联测度值分布离散情况下由点关联测度值大的点决定总体关联度倾向;②造成信息损失，平均值淹没了许多点关联测度的个性，没有充分利用点关联测度提供的丰富信息;③分辨系数的取值不同会造成关联度的排序不同。而灰关联熵分析法弥补了上述不足，从而使分析结果更加准确［5］。其计算步骤如下:

1.1 灰关联系数

X为灰关联因子集，x0［x0(1)，x0(2)，…，x0(n)］为参考列，xi［xi(1)，xi(2)，…，xi(n)］(i=1，2，…，m)为比较列，则比较列与参考列间的灰关联系数为:

1.2 灰熵

设灰内函数列x=(x1，x2，…，xm)，∀i，xi≥0，且∑xi=1，则函数:

式中:H⊗(x)为序号X的灰熵;xi为属性信息。

1.3 灰关联熵与灰熵关联度

X为离散数列，x0∈x为参考列，xi∈x(i=1，2，…，m)为比较列，Ri={ξ［x0(k)，xi(k)］k=1，2，…，n} ，则

称为分布的密度值，其中Ph∈Pi(h=1，2，…，n)。

xi的灰关联熵表示为:

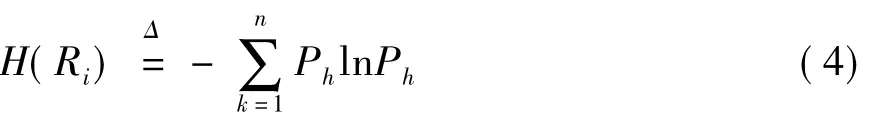
序列xi的灰熵关联度为:

式中:Hmax=lnn，代表由n个元素构成的差异信息列的最大值。

1.4 关键影响因素分析

根据灰熵关联度的排序可以得出比较列的熵关联度。关联度越大，则比较列与参考列的关联性越强，从而确定了影响因素的显著性，并进行有针对性的分析。

2 沥青混合料低温抗裂性能试验

沥青混合料的低温变形能力在很大程度上取决于沥青材料的低温性质、沥青与矿料的黏结强度、级配类型及沥青混合料的均匀性［1］。因此，笔者从沥青路面低温开裂的内因出发，选取7个典型掺量作为研究对象进行显著性定量分析。

2.1 试验原材料

2.1.1 沥青

试验采用韩国SKAH－70和中海AH－70两种重交通道路石油沥青，主要技术性能指标见表1。

表1 沥青技术性能Tab.1 Technical property of asphalt

2.1.2 矿 料

试验选用集料为花岗岩、玄武岩和花岗岩3种，填料为石灰石矿粉，经检测，各项技术指标均符合规范要求。为研究沥青与矿料间的黏附性，按照《规程》［6］将3种矿料的碱值进行测试，如表2。

表2 集料碱值测试结果Tab.2 Alkali value of aggregates

2.1.3 集料级配

采用10组AC－13集料级配(级配1～级配10)，如图1。

集料级配决定了集料颗粒间嵌挤力的大小及混合料的密实程度。良好的集料级配，有利于改善沥青混合料的使用性能。由于矿料的级配具有分形特征［7］，因此运用分形理论［8］，以分形维数表征沥青混合料级配特征，并将级配分形维数与沥青混合料的强度建立联系。

图1 集料级配曲线Fig.1 Curve of aggregate gradation

1)分形理论模型［7］

依据拓扑维数的定义，一个几何对象的维数等于确定其中一点的位置所需的坐标数目。分形对象的分维值的计算公式为:

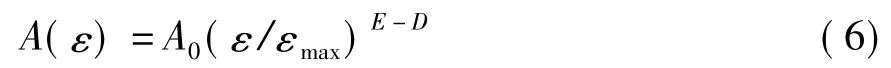
式中:E=0时，A和ε对应于点数;E=1时，A和ε对应于长度;E=2时，A和ε对应于面积和长度;E=3时，A和ε对应于体积和长度;A0为图形是整形时A的值;εmax为最大尺码长度;D为分维数值，表示研究对象的复杂程度。

2)级配集料质量分布函数的分形

定义集料质量分布函数为:

式中:P(r)为质量分布函数;m(≤r)为不大于粒径r的集料总质量;m0为集料颗粒总质量。通过推导，得出集料级配质量分布分形模型:

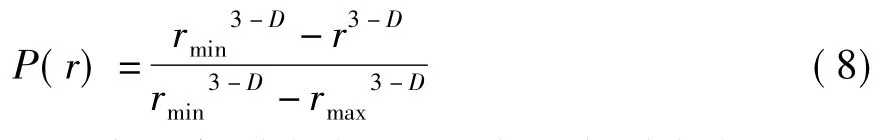
式中:rmax为最大颗粒粒径;rmin为最小颗粒粒径。

一般情况下，当颗粒粒径r相对于rmin较大时，rmin可以忽略，从而将式(8)简化为:

对式(9)两边取对数，得:

式中:D为集料级配的分形维数;C为回归参数。

3)试验级配的分形维数(表3)。

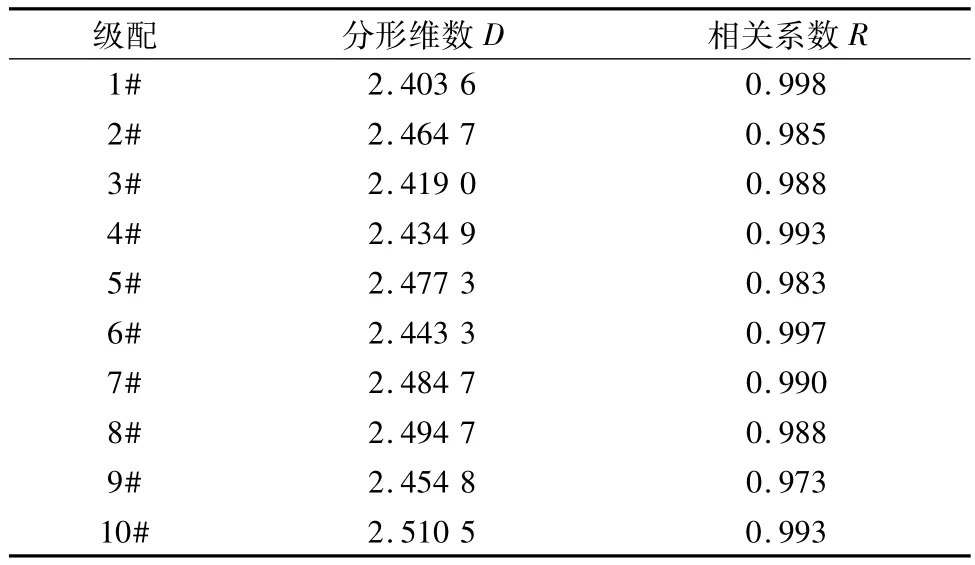
表3 集料级配的分形维数Tab.3 Fractal dimension of aggregate gradations

计算结果表明了集料的级配具有明显的分形特征，说明采用分形维数表征集料级配来研究其对沥青混合料性能的影响是合理的。

此外，4.75 mm筛孔通过率作为粗细集料的分界点，影响着集料骨架是否形成以及集料级配的分形特征，同时也与沥青混合料的结构组成形态关系密切。因此，将其作为一个影响因素进行分析是必要的。

2.2 试验结果

以临界弯拉应变评价沥青混合料低温抗裂性能，选取7个影响因素进行试验，结果见表4。

表4 低温弯曲试验结果Tab.4 Results of low －temperature bending test

3 试验结果的灰熵分析

以临界弯拉应变作为参考序列，对各影响因素进行灰关联熵分析。根据式(1)～式(5)进行计算，得到比较序列的灰熵关联度，见表5和图3。

表5 灰熵关联度Tab.5 Grey entropy correlation

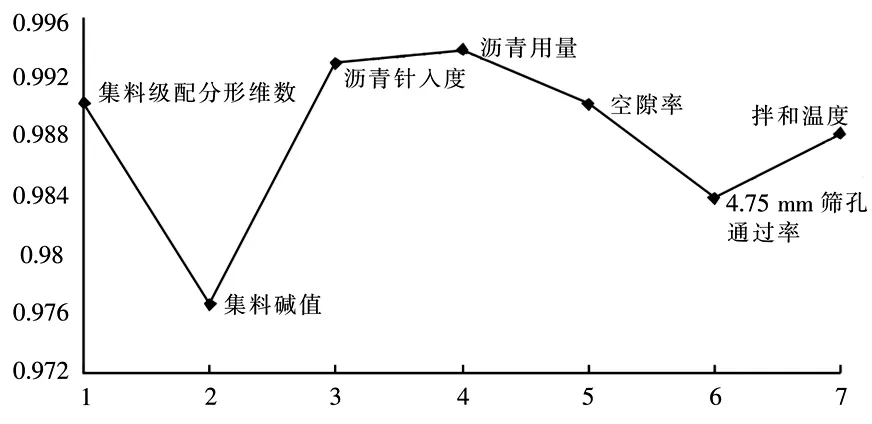
图3 不同影响因素的灰熵关联度Fig.3 Grey entropy correlation of different influencing factors

可以看出，各影响因素对沥青混合料低温抗裂性能的影响大小依次为:沥青用量＞沥青针入度＞集料级配分形维数＞空隙率＞拌和温度＞4.75 mm筛孔通过率＞集料碱值。即，就沥青混合料低温抗裂性能而言，沥青用量、沥青针入度、集料级配和空隙率是最重要的4个影响因素。

实际上，由于沥青用量的增加，沥青结合料在混合料中的比例增加，从理论上来说，沥青混合料的柔性将增加［9］。在低温和短期加载模式下，沥青呈弹性受力状态，在一定范围内，沥青用量增加使沥青膜厚度加大和混合料柔性增强，从而使沥青混合料的低温弯拉应变增大，即有利于提高沥青混合料的低温抗裂性能。因此，在满足沥青路面高温稳定性的前提下适当增加沥青用量对提高路面的低温稳定性大有裨益。

沥青针入度是我国划分沥青标号的主要依据，在一定程度上反映了沥青材料的性质。研究表明，影响沥青混合料低温开裂程度最重要的单一因素是沥青结合料的温度－劲度关系。高针入度(或低稠度)级的沥青结合料会随着温度降低产生增幅放缓的劲度，从而减少了低温开裂的可能性。由于沥青混合料的低温变形能力与其劲度模量成反比，而沥青混合料低温劲度与沥青的低温劲度密切相关，因此，采用针入度较大、稠度较低或塑性较大的沥青可以显著改善沥青混合料的低温抗裂性能。

在沥青混合料中，集料的质量分数一般在85%以上，可见对集料级配进行合理设计具有重要意义。本文涉及的集料级配分形维数是集料分布特征和空间填充能力的综合反映，较单一的控制指标更能体现出为获取良好的沥青路面使用品质，不仅要求集料形成骨架结构，而且混合料嵌挤密实。

通常，密级配沥青混合料具有较高的低温抗拉强度;同时密级配沥青混合料的空隙率较小，基于断裂力学的观点，在较密实的混合料中，空隙率小使得受外力作用形成的微裂缝在扩展时需要消耗更大的能量来克服沥青－骨料界面的黏结力，这反映了空隙率小的混合料有较好的低温抗裂性能。因此，为保证沥青路面的低温稳定性，需合理控制空隙率。

4 结语

1)运用灰熵分析法可以在“小样本”、“贫信息”的系统中评价影响系统的主次因素的显著性，从而为系统发展提供积极引导。该法克服了一般灰关联方法存在的不足，且推导较为严密，具有显著的实用价值。运用该法分析了不同因素对沥青混合料低温抗裂性能的影响显著程度。

2)分析结果表明:沥青用量、沥青针入度、集料级配和空隙率是最重要的4个影响因素。在沥青混合料配合比设计和施工时，为保证和提高沥青路面的低温稳定性，应将这4个因素作为主要控制点，并进一步考虑各因素的可控制程度和经济成本等。

［1］沈金安.沥青与沥青混合料路用性能［M］.北京:人民交通出版社，2001.

［2］郝培文，张登良，胡西宁.沥青混合料低温抗裂性能评价指标［J］.西安公路交通大学学报，2000，20(3):1 －5.

［3］邓聚龙.灰色系统理论教程［M］.武汉:华中理工大学出版社，1990.

［4］熊锐，杨锡武，杨发，等.纤维沥青混合料高温稳定性影响因素的灰关联熵分析［J］.重庆交通大学学报:自然科学版，2008，27(5):743－747.

［5］张岐山，郭喜江，邓聚龙.灰关联熵分析方法［J］.系统工程理论与实践，1996(8):7－11.

［6］JTG E 42—2005公路工程集料试验规程［S］.北京:人民交通出版社，2000.

［7］彭勇，孙力军.基于分形理论沥青混合料均匀性评价方法［J］.哈尔滨工业大学学报，2007，39(10):1656－1659.

［8］Mandelbrot B B.The fractal geometry of nature［M］.San Francisco:W H，1982.

［9］王旭东.沥青路面材料动力特征与动态参数［M］.北京:人民交通出版社，2001.