基于主成分分析法的沥青路面使用性能评价

潘怀兵

(重庆市交通规划勘察设计院，重庆401121)

路面使用性能的优劣与行车安全和运输效益息息相关，如何对其正确评价至关重要。路面的综合性能评价是一个多指标决策过程，存在评价尺度模糊性及单项指标评价结果不相容问题。针对此类问题，研究人员多采用系统分析法和回归模型法［1－3］。系统分析法以层次分析法和模糊数学方法为代表，由于人的主观因素的介入，难以得到客观公正的评价;而回归模型法在分析路况综合指标与各影响因素相互关系的基础上，建立了它们之间的函数关系数学模型，具有一定的科学性，但由于受到地域条件的限制，且有较强的经验色彩，故所得的结果亦难以满足路面综合性能多角度多属性的评价要求［4］。主成分分析法在将原始变量转变为主成分的过程中，同时形成了反映主成分和指标包含信息量的权数，以计算综合评价值，这样在指标权重选择上克服了主观因素的影响，提高了评价方法的科学性和适用性。鉴于此，笔者选用主成分分析法进行沥青路面使用性能评价是可行的。

1 主成分分析法介绍

主成分分析法是通过恰当的数学变换，使新变量——主成分成为原变量的线性组合，并选取少数几个在变差总信息量中比例较大的主成分来分析事物的一种方法。主成分在变差信息量中的比例越大，则在综合评价中的作用就越大。该法不仅可消除评价指标之间的相关影响，并减少指标选择的工作量，而且计算过程可用数学软件进行简化，计算过程快捷、结果精确。主成分分析法的算法步骤介绍如下［5］。

1.1 原始指标数据的标准化处理

设有n个样本，p项指标，可得数据矩阵X=(Xij)n×p，i=1，2，…，j=1，2，…，Xij表示第i个样本的第j项指标值。用Z-score法对数据进行标准化变换:

1.2 求指标数据的相关矩阵

R=(rjk)p×p，j=1，2，…，p，k=1，2，…，其中p，rjk为指标j与指标k的相关系数。

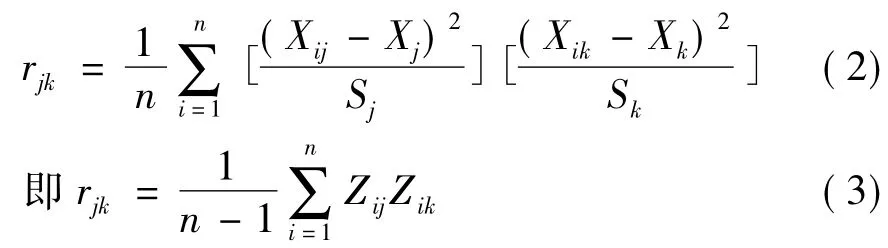
其中:rij=1;rjk=rkj;i=1，2，…，n;j=1，2，…，p。

1.3 求相关矩阵R的特征根、特征向量，确定主成分

其中:g=1，2，…，p;F1称为第1主成分;F2称为第2主成分;…;Fp称为第p主成分。

1.4 求方差贡献率，确定主成分个数

一般主成分个数等于原始指标个数，如果原始指标个数较多，进行综合评价时就比较麻烦。主成分分析法就是选取尽量少的k个主成分(k＜p)来进行综合评价，同时还要使损失的信息量尽可能少。k值由式(5)方差贡献率决定。

1. 5 对k 个主成分进行综合评价

先求每一个主成分的线性加权值Fg=lg1Z1+lg2Z2+，…，+lgpZp，g=1，2，… ，k，再对k个主成分进行加权求和，即得最终评价值，权数为每个主成分的方差贡献率:最终评价值为:

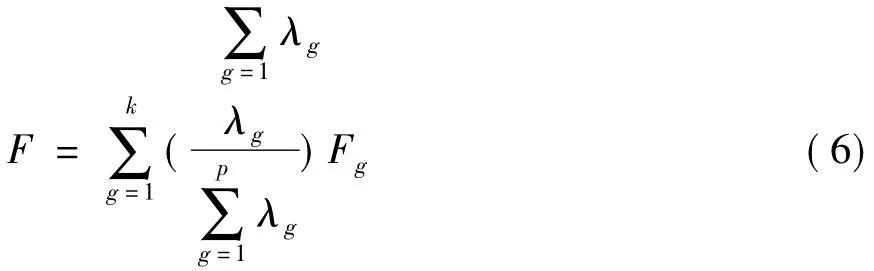
2 沥青路面使用性能评价

2.1 路面性能评价指标体系及评价标准

评价指标是为了达到系统的目的，从系统众多的输出特性中选出的整套衡量指标，是对现实复杂系统的一种简化［6］。在路面性能综合评价中，常用的评价指标有路况指数PCI、强度指数SSI、行驶质量指数RQI和摆值BPN。JTJ 073.2—2001《公路沥青路面养护技术规范》［7］中确定了各评价指标的评价标准，如表1。

表1 沥青路面性能各指标评价标准Tab.1 Evaluation standards of various indexes of asphalt pavement performance

2.2 案例评价

以文献［8］中某段公路沥青路面的调查数据(表2)为例，利用主成分分析法对其进行路况综合评价。

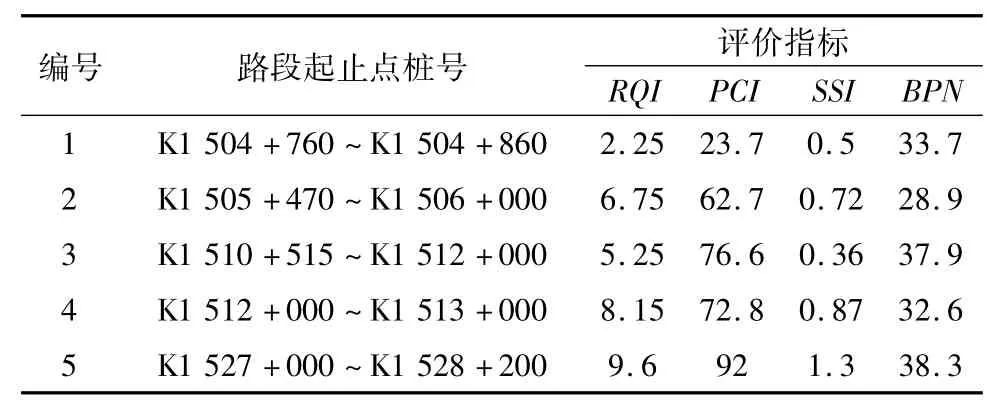
表2 路段各分项指标值Tab.2 Various subitems index value for each road segment

将表2的数据按照主成分分析法中数据标准化处理后，采用Matlab数学工具［9］计算出各个指标间的相关系数矩阵见表3。

表3 相关系数矩阵Tab.3 Coefficient matrix

由相关系数矩阵计算出特征值和特征向量，以及各个指标的贡献率和累计贡献率见表4。

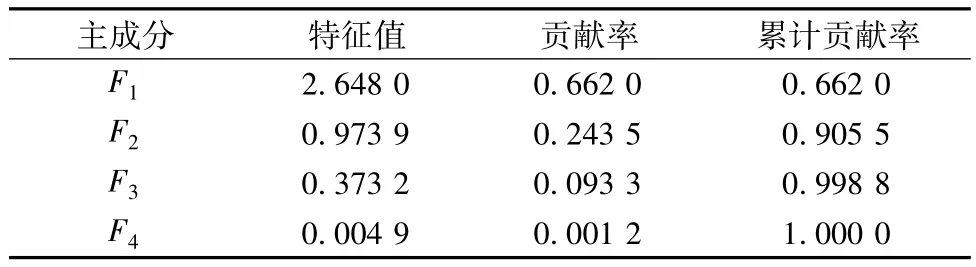
表4 特征值、贡献率及累计贡献率Tab.4 Eigenvalue，contribution rate and cumulative contribution rate

由表4可看出，前面2个主成分的累计贡献率高达90%。由此可知，只要用第1、第2两个主成分就可以很好地解释原始数据了。取前两个主成分的特征值对应的特征向量见表5。

表5 两个主成分的特征值对应的特征向量Tab.5 Corresponding eigenvector of two eigenvalues

由此可得这两个主成分的线性组合如下:

则沥青路面使用性能综合评价值为:

这样，沥青路面使用性能评价指标就可以精简为3个。将表1数据代入公式(9)计算后作为上下限，得出新的沥青路面使用性能评价标准，见表6。

表6 沥青路面使用性能评价标准Tab.6 Performance evaluation criteria of asphalt pavement

将表2中的各分指标值代入式(9)计算，可得各路段的综合评价值。如表7，各路段的评价结果分别为:中、中、良、良、优。

表7 各路段路基面性能综合评价值Tab.7 Synthetical evaluation F for each road segment

与文献［8］利用能够较全面评价各因素影响程度的灰色聚类决策评价方法所得结果(次、中、良、良、优)相比较，可知虽采用不同的方法，但得到的结论大致相同，表明用主成分分析法进行路面使用性能评价是可行的。

3 结语

1)主成分分析法是一种较为客观的综合评价方法，它根据各项指标的相关关系和变异程度来确定权重，并计算综合评价值，大大减少了指标选择的工作量。本文中计算指标由原定的4个减为2个，在信息量损失很少的情况下，简化了分析过程。

2)当选择指标较多且各指标间存在的相关性会使计算结果产生累加效应时，采用主观性较强的方法不仅过程繁杂，而且评价结果失真;但采用主成分分析法则能有效地克服这类缺点。因此，将该法应用到公路沥青路面使用性能综合评价上，可获得较为客观和准确的结论，从而为科学制定沥青路面养护决策提供依据。

3)值得注意的是，主成分分析法也有其缺点，即不能单一地去评价某一路面的使用性能，因此应根据具体情况进行选择，如该法与其他方法的组合。

［1］李艳双，曾珍香，张闽，等.主成分分析法在多指标综合评价方法中的应用［J］.河北工业大学学报，1999，28(1):94 －97.

［2］陆亚兴.柔性路面损坏状况综合评价的AHP－Fuzzy方法［J］.重庆交通学院学报，1992，11(2):81 －88.

［3］Michael I D.Concrete pavement evaluation system(Copes) －national prediction model demonstration［C］//Proceeding of 3rd International Conference on Concrete Pavement Design.Purdue:Purdue University，1985.

［4］杨明，阳亮.主成分分析法在高速公路沥青路面使用性能评价中的应用［J］.中南公路工程，2006，31(6):55 －89.

［5］张文峰，史忠科.主成分分析法在城市道路交通安全评价中的应用［J］.计算机工程与应用，2007，43(36):246 －248.

［6］韩传峰，刘亮，王忠礼.基于物元分析法基础设施系统可持续性评价［J］.中国人口资源与环境，2009，19(2):116 －121.

［7］JTJ 073.2—2001公路沥青路面养护技术规范［S］.北京:人民交通出版社，2001.

［8］李清富，胡群芳，刘文，等.基于灰色聚类决策的沥青路面使用性能评价［J］.郑州大学学报:工学版，2003，24(2):44 －47.

［9］陈仲生.基于Matlab7.0的统计信息处理［M］.长沙:湖南科学技术出版社，2005.