N—O键解离焓的密度泛函理论研究

郑文锐 徐菁利 熊 瑞

(上海工程技术大学化学化工学院,上海 201620)

N—O键解离焓的密度泛函理论研究

郑文锐*徐菁利*熊 瑞

(上海工程技术大学化学化工学院,上海 201620)

在高精度计算方法G3和G3B3的基础上,比较了密度泛函理论(DFT)十几种方法对N—O键解离焓(BDE)相对于实验值的计算精度,发现用B3P86方法计算15种化合物N—O键的BDE,均方根误差最小,仅为6.36 kJ·mol-1,计算值与实验值的线性相关系数为0.991.在此基础上,用该方法分别计算了非芳香化合物及芳香化合物的N—O键BDE.通过自然键轨道分析,发现部分N—O键的BDE与N—O键的键长、原子电荷密度及键级之间存在定量关系.此外,在B3P86方法的基础上预测了几种典型的杂环芳香化合物N—O键BDE值.

密度泛函理论;键解离焓;自然键轨道分析;N—O键

在化学及生物化学过程中,总是包含着旧键的断裂以及新键的生成,因此需要大量的化学键均裂解离焓(BDE)的热力学数据.用来测定化合物化学键解离焓的实验方法较多,自由基动力学方法、光致电离质谱分析技术和酸性/电子亲和性循环方法是目前广泛运用的气相测定方法[1].电化学循环和光声热量测定技术是液相测定键解离焓常用的方法[2].但由于实验方法本身的缺陷和自由基寿命较短等原因导致实验测定键解离焓仍然存在困难,获得的某些键解离焓无法验证其可靠性,目前获得精确的键解离焓的另一种可行方法是利用量子化学计算[3].

其中,从头算方法比一些经验及半经验方法更受欢迎,而Hartree-Fock及微扰理论由于在处理开壳层体系时存在自旋污染不适合BDE值的计算[4].高水平的从头算方法如耦合簇理论方法(CCSD),组态相关方法(QCISD)计算的BDE值比Hartree-Fock及微扰理论方法要好,但研究表明,当采用的基组不够大时,这些高水平的理论方法仍然大大低估了BDE值[5].组合从头算方法例如G3,CBS-Q方法虽能成功地用于BDE的计算[4],但是只适用于处理含有不超过8个非氢原子的体系.密度泛函理论(DFT)方法比组合从头算方法更经济,且不受自旋污染的影响,因此DFT方法近年来越来越普遍地运用到BDE的计算中[6].

N—O键是一类非常重要的键型,含有N—O键的化合物在生物医药领域具有重要的研究意义,例如,芳香杂环的氮氧化物被认为在临床治疗肿瘤方面具有一定的作用,这些化合物本身并不活泼,然而在体内酶的作用下能生成自由基中间体并导致细胞毒素的DNA链断裂.而生成自由基中间体的难易与N—O键BDE有关[7].罗渝然[8]搜集了大量的有机化合物的BDE实验数据,然而对于N—O键的BDE数据非常有限,而且有些实验值值得怀疑,例如对于R3N—O的N—O键,当R为CH3,C2H5,n-C4H9时,键解离焓的实验值分别为(256±5),(67±5), (-74±6)kJ·mol-1[9].取代基R均为烷基,且烷基链长相差不大,然而其BDE的实验值却相差很大.且R为正丁基时,其BDE数值为负.对于N—O键BDE的理论研究,Gomes等[7]运用B3LYP方法研究了喹喔啉-1,4二氧化物的N—O键能的取代基效应,并分析了N—O键BDE对一些化合物的抗肿瘤活性的影响.Gomes等[10]还研究了吩嗪类二氮氧化物衍生物的N—O键BDE,理论计算采用B3LYP方法. Ribeiro da Silva等[11-12]结合实验和理论研究,讨论了喹喔啉类二氧化物衍生物的热力学性质,其中包括N—O键BDE,理论计算结果与实验结果具有较好的一致性.

然而,对于N—O键BDE的系统的理论研究目前还尚未见报道.因此,本文首先通过比较不同密度泛函理论方法对N—O键BDE的计算结果,找出一种精度较高的方法,在此方法的基础上对N—O键BDE进行系统的研究.不仅可以进一步验证实验数据的可靠性,还能从理论角度探讨N—O键BDE的影响因素.

1 计算方法

键均裂解离焓值BDE是通过101325 Pa,298 K气相条件下反应X—Y→X·+Y·的焓变值来进行计算的,其中反应物分子和生成物自由基在101325 Pa,298 K条件下的焓值由式H298=E+ZPE+Htrans+Hrot+ Hvib+RT获得,其中,E为电子能量,ZPE为零点能,是对分子电子能量的校正;Htrans,Hrot,Hvib分别表示平动、转动和振动对能量的贡献;RT项为焓值的温度校正项.所有分子及自由基在B3LYP/6-31+G(d)的水平下进行全优化,所有构象经过相同水平下的频率计算以证实为稳定构象,即所有的振动频率值为正,无虚频存在.分别采用B3LYP[13],X3LYP[14], BMK[15],B3P86[16],MPW1B95[17],PBE1W[18],TPSS1-KCIS[19],MPW1K[20],MPW3LYP[17],TPSSLYP1W[18], MPW1KCIS[21],B2PLYP[22],MPW2PLYP[23],KMLYP[24], MPW1P86[25],O3LYP[26],MPWLYP1M[27]十七种DFT方法对分子及自由基进行单点能的计算,综合考虑基组大小对计算精度的影响以及计算机时,单点能的计算基组使用6-311++G(2df,2p).在B3LYP/6-31+ G(d)优化的基础上再用B3P86/6-31+G(d)方法进行自然键轨道(NBO)分析[28].所有计算采用Gaussian 03程序包[29].

2 结果与讨论

2.1 各种DFT方法的性能评估

我们选取了16个分子的N—O键BDE的实验值[8]作为参考,先运用高精度理论方法 G3[30]和G3B3[31]来计算其BDE,并与实验值进行比较.但是由于计算方法的限制,所选分子的重原子数都不超过8.实验值[8]及G3、G3B3的计算结果见表1,表中还列出了平均偏差(MD),平均绝对偏差(MAD)及均方根误差(RMSE)的值.

从表中可以看出,除了HO—N═CHCH3BDE的G3和G3B3计算值均与实验值相差超过了25 kJ·mol-1外,其余15个G3和G3B3的计算结果与实验值都吻合得较好,因此,分子HO—N═CHCH3BDE的实验值是值得质疑的.除去这个相差较大的BDE值,从其他BDE的MD,MAD和RMSE值可以看出,G3B3方法的均方根误差仅为3.83 kJ·mol-1,比G3的结果4.42 kJ·mol-1低.因此G3B3的结果略好于G3.其理论值与实验值的线性相关性见图1.从图1可以看出,对于15个分子的N—O BDE的计算,G3B3与实验值的线性相关系数为0.997.

我们选取了B3LYP等十几种DFT方法来计算这15个分子的N—O键BDE值,不同DFT方法的MAD,MD和RMSE列于表2.可以看出,B3P86方法的MAD和RMSE均最小,分别为5.49和6.36 kJ·mol-1,MD为-2.14 kJ·mol-1.B3P86方法指定的是Becke三参数混合泛函,非局域相关由Perdew 86提供.结果证明对于计算N—O键BDE,B3P86具有较高的计算精度,其计算精度的可靠性可能与其本身的函数形式有关.使用最多的B3LYP泛函方法的RMSE为25.44 kJ·mol-1,并且都低估了每一个N—O键的BDE值,其MD和MAD在数值上相等. BMK方法是2004年由Boese和Martin发展起来的一种新泛函,对于C—H键的BDE具有较好的计算精度[32],然而对于N—O键BDE的计算,其结果并非最理想.其中,MPW1K方法对N—O键BDE的计算RMSE最大,为36.43 kJ·mol-1.此外我们还采用限制性开壳层方法ROB3P86对自由基进行单点能计算,其RMSE为10.97 kJ·mol-1.因此对于自由基的单点能计算,仍是采用默认的(U)B3P86方法的结果较好.B3P86方法的计算值与实验值的线性相关性见图2.从图2可以看出,对于15个分

子的N—O BDE的计算,B3P86计算值与实验值的线性相关系数为0.991.由以上分析,对以下N—O键BDE的计算采用B3P86/6-311++G(2df,2p)//B3LYP/ 6-31+G(d)方法.

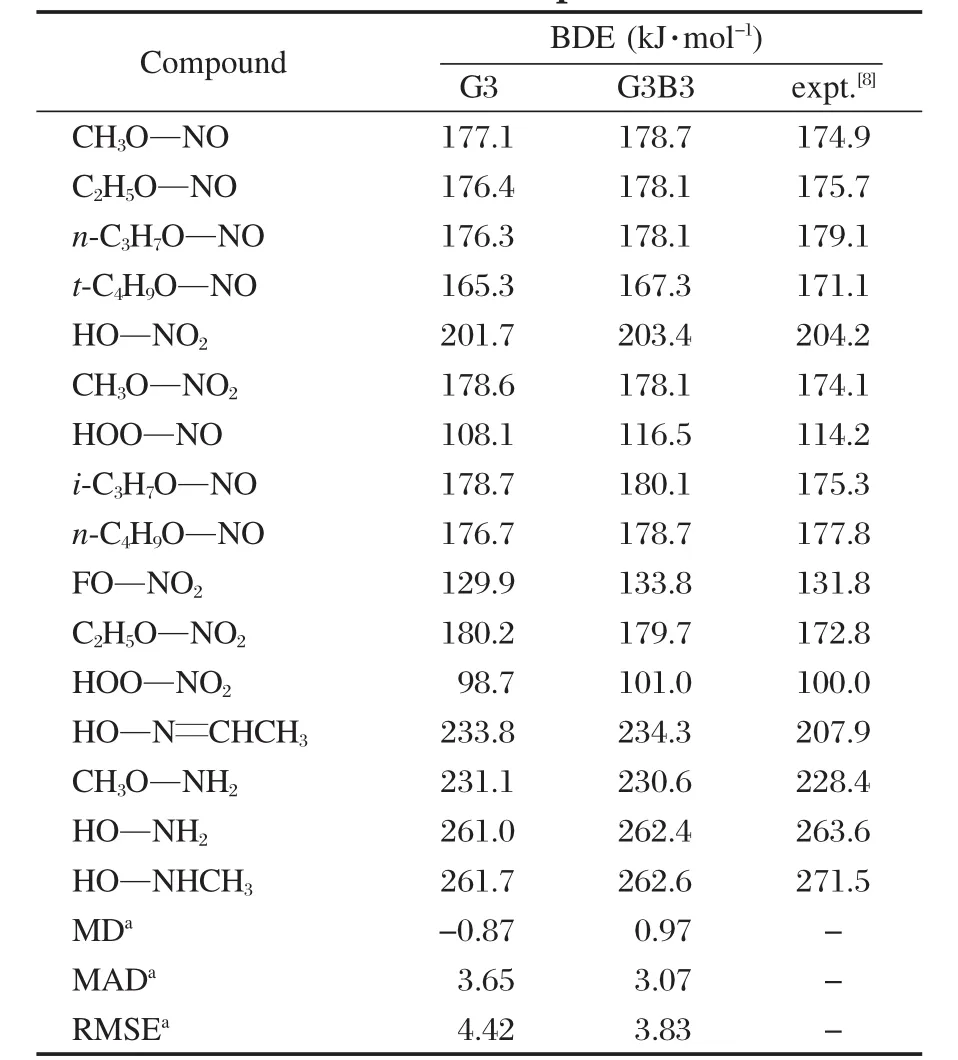
表1 16个G3、G3B3计算及实验N—O键解离焓值Table 1 Experimental and G3,G3B3 calcuated N—O BDEs for 16 compounds

图1 G3B3计算与实验的N—O的BDE值之间的相关关系Fig.1 Correlation between the experimental and G3B3 calculated N—O BDEs

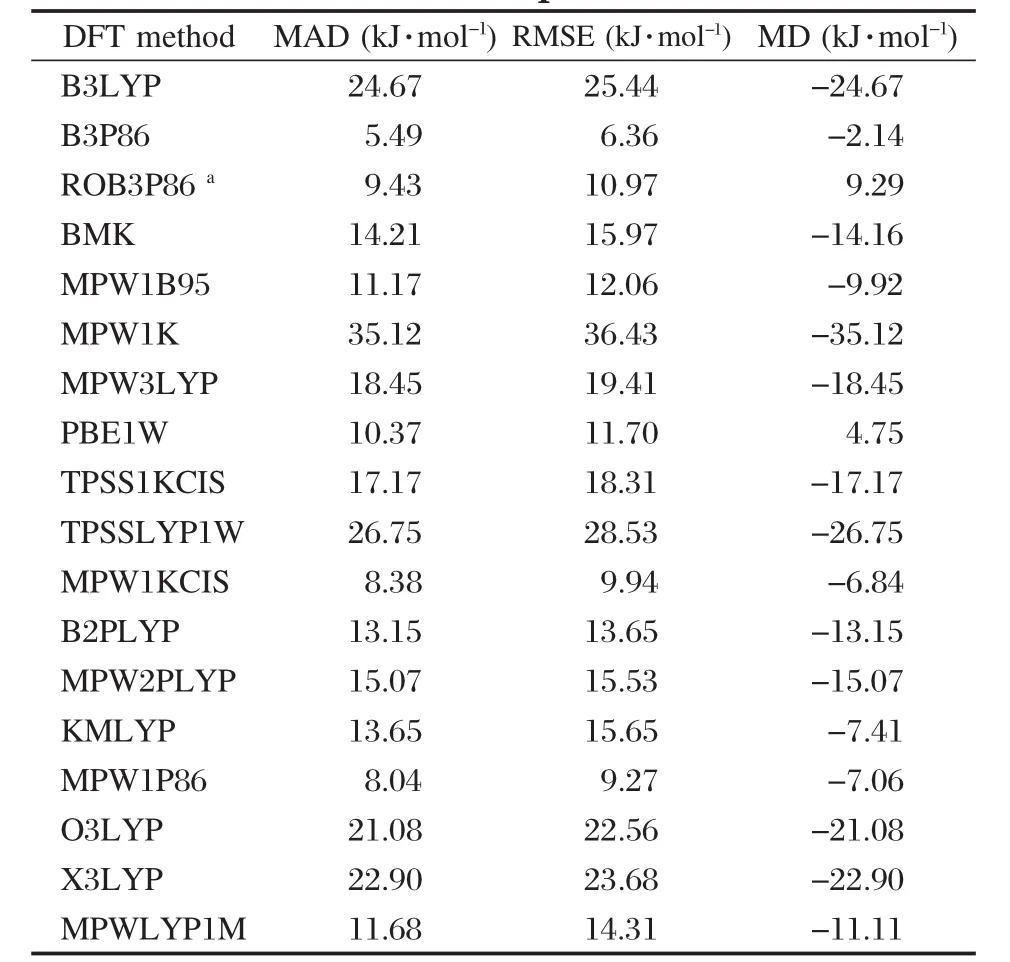
表2 不同密度泛函理论方法计算BDE值与实验BDE值的比较Table 2 Comparison of calculated BDEs by different DFT methods with experimental values

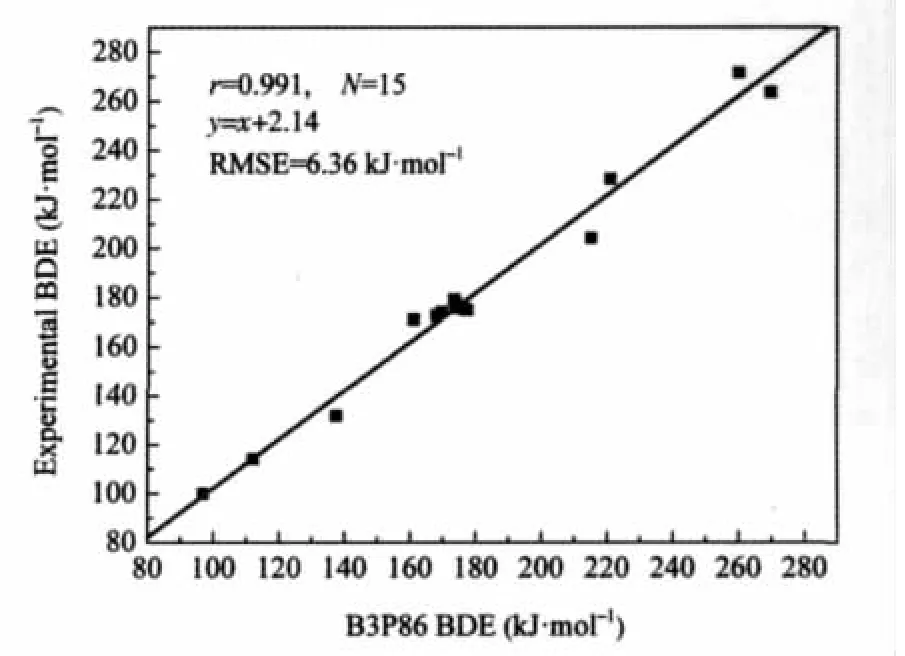
图2 B3P86计算与实验的N—O的BDE值之间的相关关系Fig.2 Correlation between the experimental and B3P86 calculated N—O BDEs

2.2 非芳香化合物的N—O键BDE

我们用B3P86方法计算了21个非芳香类化合物的N—O键BDE,结果列于表3.表中还列出了计算的N—O键的键长数据.

从表中可看出,B3P86计算值与实验值相差20 kJ·mol-1以上的化合物有6个,分别为:(1)FO—NO(No.1),实验值与计算值相差20.1 kJ·mol-1;(2) C2H5OO—NO2(No.12),实验值与计算值相差21.7 kJ· mol-1;(3)CH2═C(CH3)OO—NO2(No.14),实验值与计算值相差33.1 kJ·mol-1;(4)C2H5COO—NO(No.16),实验值与计算值相差33.7 kJ·mol-1;(5)(C2H5)3N—O (No.19),实验值与计算值相差高达184.9 kJ·mol-1;(6) (n-C4H9)3N—O(No.20),实验值与计算值相差高达309.4 kJ·mol-1.其中,(CH3)3N—O,(C2H5)3N—O及(n-C4H9)3N—O属于同一系列化合物,只是取代烷基碳链不同,实验值却相差很大,分别为256.0,67.0及-74.0kJ·mol-1[8-9].但是B3P86计算值分别为239.1, 251.9及235.4 kJ·mol-1,彼此相差不大.从数据看,我们认为计算值更为合理,因此对(C2H5)3N—O与(n-C4H9)3N—O的实验N—O键BDE值提出质疑.这两种物质N—O键BDE的实验数据,文献中采用的是量热法[9],其中(n-C4H9)3N—O的实验N—O键BDE值为负值,Acree等[33]认为键解离焓值不可能为负,因此该实验数据不能被接受.

表3 21个非芳香化合物的B3P86计算及实验N—O键解离焓值Table 3 Experimental and B3P86 N—O BDEs for 21 non-aromatic compounds

图3 表3中O—NO型分子N—O键BDE与N—O键长的相关关系Fig.3 Relationship between the N—O BDEs and N—O bond length of O—NO molecules in Table 3

表3中的N—O键主要包括三种类型:O—NO型,O—NO2型及具有双键性质的N—O型.对于其中6个O—NO型N—O键,N—O单键的键长与BDE计算值之间存在线性关系,其线性相关系数的平方值即r2为0.968.如图3所示.而对于O—NO2型及具有双键性质的N—O型的N—O键BDE计算值与N—O键键长之间不存在明显的线性关系.

对于同一系列的化合物,如i-C4H9O—NO和s-C4H9O—NO,N—O键BDE的计算值相差不大,分别为170.8及176.3 kJ·mol-1.即当氧端取代基为烷基时,烷基的改变对N—O键BDE的影响不大,类似的还有C3H7O—NO2和i-C3H7O—NO2,BDE的计算值也相差不大.表中还能看出不同的吸电子取代基和给电子取代基对N—O键BDE的影响情况,例如CH3OO—NO2和CF3OO—NO2,BDE的计算值分别为90.7及100.9 kJ·mol-1,这是由于CH3为给电子取代基,CF3为吸电子取代基,因此N—O键断裂所生成的相应自由基CH3OO·比CF3OO·更稳定,所以对应的分子CH3OO—NO2中的N—O键的BDE小于CF3OO—NO2.

2.3 芳香化合物的N—O键BDE

我们用B3P86方法计算了19个芳香化合物的N—O键BDE,结果列于表4.

从表中可以看出,对于这19种芳香化合物N—O键BDE的计算,有1个化合物(No.13)实验值与B3P86计算值的偏差较大,为20 kJ·mol-1,其余化合物的计算值与实验值偏差均在20 kJ·mol-1以内.例如,No.5,B3P86计算值(290.8 kJ·mol-1)与实验值(301.7 kJ·mol-1)较为接近;No.6,B3P86计算值(287.8 kJ·mol-1)与实验值(274.7 kJ·mol-1)较为接近;No. 19,B3P86计算值(287.4 kJ·mol-1)与实验值(294.8 kJ·mol-1)较为接近.其中,有些化合物的实验BDE被重复测量过,不同的实验值之间本身偏差也较大.

表4 19个芳香化合物的B3P86计算及实验N—O键解离焓值Table 4 B3P86 calculated and experimental N—O BDEs for 19 aromatic compounds

图4 电荷乘积N—O键BDE与qNqO的相关关系Fig.4 Relationship between the N—O BDEs and qNqO

苯环上的远程取代基对N—O键的影响不显著,如No.1-No.4,当苯环上对位取代基为吸电子和给电子取代基时,吸电子取代基(如硝基)对应的BDE较给电子取代基(如甲基)的大,但差别不大,不超过5 kJ·mol-1.同样的规律在No.13-No.15及No.16-No.19中也得到体现,苯环上邻位和对位取代基的吸电子及给电子效应对BDE的影响均不大,但是α取代基效应较为明显,如No.13与No.16,N原子α位为正丁基和苯基时,BDE值差别较大,正丁基取代的较苯基取代的BDE大,此处体现了苯基取代基较强的给电子共轭效应,即对应的自由基稳定性较大导致BDE较小.在所有的氮氧化物中(No.5-No. 19),No.12的BDE值最小,同样也体现了较大的α取代基效应.

经过NBO分析,表中同时列出了N—O键N原子和O原子的自然电荷密度及以Wiberg键级表示的N—O键键级,即WBI(Wiberg bond index)[34].从键级可以看出,No.1-No.4的WBI值在0.8左右,为单键,No.5-No.19的WBI均大于1,在1.2-1.4之间,具有部分双键性质.此外,我们发现,对于表4中所有N—O键BDE的B3P86理论值,不仅与N—O键氮原子和氧原子的自然电荷密度的乘积呈现线性关系,相关系数为0.966;而且也与WBI值呈现线性关系,相关系数为0.967,线性相关图分别见图4和图5.

表4中的化合物可分为两类,一类为No.1-No. 4,断裂的N—O键为单键,此外,氮原子还以双键与氧原子结合,氮原子2s轨道的两个电子未参与成键,其BDE计算值的范围在138.9-143.8 kJ·mol-1之间;另一类为氮氧化物,为No.5-No.19,断裂的N—O键具有双键特征,氮原子2s轨道的两个电子参与成键,分子中形成了不定域π键,其BDE计算值的范围在244.3-303.7 kJ·mol-1之间,远远大于第一类化合物.可以看出,N—O键的不同成键特征对其BDE有较大的影响,离域π键的形成使得N—O键较难断裂,BDE值较大.

图5 N—O键BDE与N—O键键级的相关关系Fig.5 Relationship between BDEs and WBI of N—O

2.4 几种典型芳香杂环氮氧化物的N—O键BDE预测

由于芳香杂环的氮氧化物被认为在临床治疗肿瘤方面具有一定的作用,其N—O键的BDE对研究作用机理有一定的指导意义,我们用B3P86方法预测了几种典型芳香杂环氮氧化物的N—O键BDE,结果列于表5.

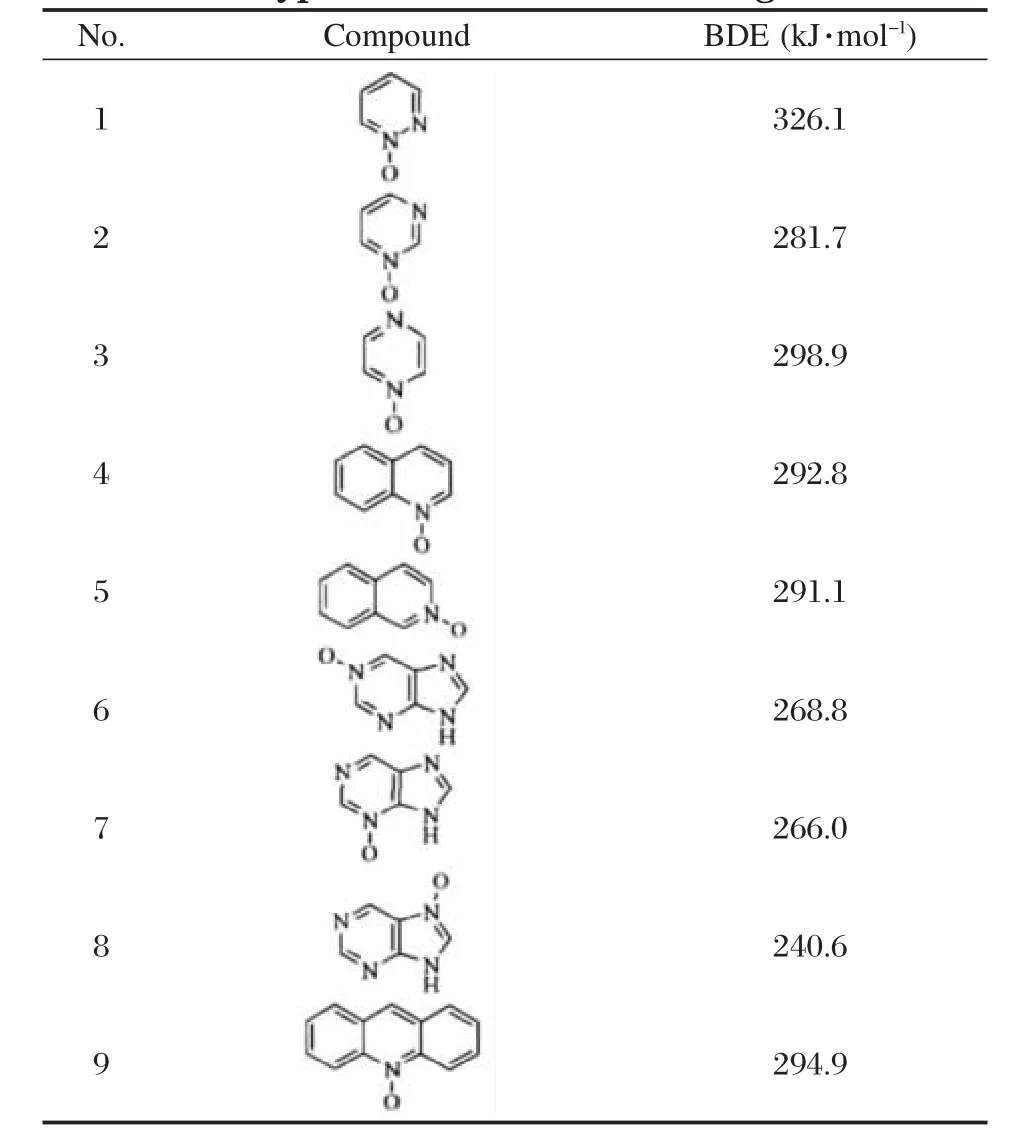
表5 9种典型芳香杂环氮氧化物N—O键BDE的B3P86理论预测值Table 5 B3P86 theoretical prediction values of N—O BDE for 9 typical heteroaromatic nitrogen oxides

从表中可以看出,含有2个氮原子的六元氮杂环其氮氧化物的N—O键BDE值与环上两个氮原子的相对位置有关,即No.1-No.3,其BDE值大小顺序为哒嗪＞吡嗪＞嘧啶,即两个氮原子处于邻位时,其BDE值最大,处于间位时,其BDE最小,最大值与最小值之间相差25 kJ·mol-1以上.No.4及No.5的喹啉氮氧化物和异喹啉氮氧化物的BDE值差别不大,说明其BDE值受氮原子在环上的位置影响不大.这一规律也在嘌呤环上得到证实,即No.6-No.8,六元环上的N原子位置不影响其N—O键BDE,而五元环位置上的氮原子其N—O键BDE与六元环位置的BDE相差25 kJ·mol-1以上,说明环的类型对BDE的影响较大.吖啶环氮氧化物(No.9)的BDE与喹啉环氮氧化物(No.4)的BDE相差不大,也体现了远程取代基效应不明显的规律.

3 结 论

在高精度计算方法G3和G3B3的基础上,比较了十几种DFT方法对N—O键BDE的计算精度,发现B3P86方法对于15种化合物N—O键BDE的计算,均方根误差最小,为6.36 kJ·mol-1,计算值与实验值的线性相关系数为0.991.在此基础上,用该方法分别计算了非芳香化合物及芳香化合物的N—O键BDE,对某些实验值提出了质疑,计算结果还体现了不明显的远程取代基效应及较明显的α取代基效应,同时通过自然键轨道分析,发现部分N—O键的BDE与N—O键的键长、原子电荷密度及键级之间均存在定量关系.此外,鉴于芳香杂环的氮氧化物在临床治疗肿瘤方面的重要作用,在B3P86方法的基础上预测了几种典型的杂环芳香化合物N—O键BDE值.

1 (a)Berkowitz,J.;Ellison,G.B.;Gutman,D.J.Phys.Chem.,1994, 98:2744 (b)Zhu,X.Q.;Li,H.R.;Ai,T.;Lu,J.Y.;Yang,Y.;Cheng,J.P. Chem.-Eur.J.,2003,9:871

2 (a)Bordwell,F.H.;Zhang,X.M.Acc.Chem.Res.,1993,26:510 (b)Larhoven,L.J.J.;Mulder,P.;Wayner,D.D.M.Acc.Chem. Res.,1999,32:342

3 (a)Sun,Y.M.;Zhang,H.Y.;Chen,D.Z.;Liu,C.B.Org.Lett., 2002,4:2909 (b)Wang,L.F.;Zhang,H.Y.Bioorg.Med.Chem.Lett.,2003,13: 3789 (c)Yao,X.Q.;Hou,X.J.;Jiao,H.;Xiang,H.M.;Li,Y.W. J.Phys.Chem.A,2003,107:9991 (d)Turecek,F.J.Am.Chem.Soc.,2003,125:5954 (e)Shen,L.;Zhang,H.Y.;Ji,H.F.Org.Lett.,2005,7:243

4 (a)Feng,Y.;Liu,L.;Wang,J.T.;Huang,H.;Guo,Q.X.J.Chem. Inf.Comput.Sci.,2003,43:2005 (b)Qi,X.J.;Li,Z.;Fu,Y.;Guo,Q.X.;Liu,L.Organometallics, 2008,27:2688

5 (a)Henry,D.J.;Parkinson,C.J.;Mayer,P.M.;Radom,L.J.Phys. Chem.A,2001,105:6750 (b)Song,K.S.;Cheng,Y.H.;Fu,Y.;Liu,L.;Li,X.S.;Guo,Q.X. J.Phys.Chem.A,2002,106:6651

6 (a)Pratt,D.A.;Mills,J.H.;Porter,N.A.J.Am.Chem.Soc.,2003, 125:5801 (b)Zhang,H.Y.;Sun,Y.M.;Wang,X.L.Chem.Eur.J.,2003,9: 502 (c)Lin,C.L.;Lai,C.H.;Chu,S.Y.Chem.Phys.Lett.,2002,359: 355 (d)Zhang,H.Y.;Sun,Y.M.;Chen,D.Z.Chin.Chem.Lett.,2002, 13:531 (e)Yao,X.Q.;Hou,X.J.;Wu,G.S.;Xu,Y.Y.;Xiang,H.W.; Jiao,H.;Li,Y.W.J.Phys.Chem.A,2002,106:7184 (f)Lue,J.M.;Wittbrodt,J.M.;Wang,K.;Wen,Z.;Schlegel,H. B.;Wang,P.G.;Cheng,J.P.J.Am.Chem.Soc.,2001,123:2903 (g)Feng,Y.;Liu,L.;Wang,J.T.;Zhao,S.W.;Guo,Q.X.J.Org. Chem.,2004,69:3129

7 Gomes,J.R.B.;Ribeiro da Silva,M.D.M.C.;Ribeiro da Silva, M.A.V.Chem.Phys.Lett.,2006,429:18

8 Luo,Y.R.Handbook of bond dissociation energies.Beijing: Science Press,2005:212-219 [罗渝然.化学键能数据手册.北京:科学出版社,2005:212-219]

9 Acree Jr.,W.E.;Tucker,S.A.;Ribeiro da Silva,M.D.M.C.; Matos,M.A.R.;Goncalves,J.M.;Ribeiro da Silva,M.A.V.; Pilcher,G.J.Chem.Thermody.,1995,27:391

10 Gomes,J.R.B.;Sousa,E.A.;Goncalves,J.M.;Monte,M.J.S.; Gomes,P.;Pandey,S.;Acree Jr.,W.E.;Ribeiro da Silva,M.D.M. C.J.Phys.Chem.B,2005,109:16188

11 Ribeiro da Silva,M.D.M.C.;Gomes,J.R.B.;Goncalves,J.M.; Sousa,E.A.;Pandey,S.;Acree Jr.,W.E.Org.Biomol.Chem., 2004,2:2507

12 Ribeiro da Silva,M.D.M.C.;Gomes,J.R.B.;Goncalves,J.M.; Sousa,E.A.;Pandey,S.;Acree Jr.,W.E.J.Org.Chem.,2004,69: 2785

13 (a)Becke,A.D.Phys.Rev.A,1988,38:3098 (b)Lee,C.;Yang,W.;Parr,R.G.Phys.Rev.B,1988,37:785

14 Xu,X.;Goddard,W.A.Proc.Natl.Acad.Sci.U.S.A.,2004,101: 2673

15 Boese,A.D.;Martin,J.M.L.J.Chem.Phys.,2004,121:3405

16 Perdew,J.P.Phys.Rev.B,1986,33:8822

17 Zhao,Y.;Truhlar,D.G.J.Phys.Chem.A,2004,108:6908

18 Dahlke,E.E.;Truhlar,D.G.J.Phys.Chem.B,2005,109:15677

19 Zhao,Y.;Truhlar,D.G.Phys.Chem.Chem.Phys.,2005,7:2701

20 Lynch,B.J.;Zhao,Y.;Truhlar,D.G.J.Phys.Chem.A,2003, 107:1384

21 Zhao,Y.;Gonzalez-Garcia,N.;Truhlar,D.G.J.Phys.Chem.A, 2005,109:2012

22 Grimme,S.J.Chem.Phys.,2006,124:10342

23 Schwabe,T.;Grimme,S.Phys.Chem.Chem.Phys.,2006,8:4398

24 Kang,J.K.;Musgrave,C.B.J.Chem.Phys.,2001,115:11040

25 Perdew,J.P.;Burke,K.;Wang,Y.Phys.Rev.B,1996,54:16533

26 Hoe,W.M.;Cohen,A.J.;Handy,N.C.Chem.Phys.Lett.,2001, 341:319

27 Schultz-Fademrecht,C.;Tius,M.A.;Grimme,S.;Wibbeling,B.; Hoppe,D.Angew.Chem.Int.Edit.,2002,41:1532

28 (a)Reed,A.E.;Curtiss,L.A.;Weinhold,F.Chem.Rev.,1988,88: 899 (b)Cheng,Y.H.;Zhao,X.;Song,K.S.;Liu,L.;Guo,Q.X.J.Org. Chem.,2002,67:6638

29 Frisch,M.J.;Trucks,G.W.;Schlegel,H.B.;et al.Gaussian 03. Revision A.01.Pittsburgh,PA:Gaussian Inc.,2003

30 Curtiss,L.A.;Raghavachari,K.;Redfern,P.C.;Rassolov,V.; Pople,J.A.J.Chem.Phys.,1998,109:7764

31 Baboul,A.G.;Curtiss,L.A.;Redfern,P.C.;Raghavachari,K. J.Chem.Phys.,1999,110:7650

32 Zheng,W.R.;Fu,Y.;Wang,H.J.;Guo,Q.X.Chin.J.Org.Chem., 2008,28:459 [郑文锐,傅 尧,王华静,郭庆祥.有机化学, 2008,28:459]

33 Acree Jr.,W.E.;Pilcher,G.;Ribeiro da Silva,M.D.M.C.J.Phys. Chem.Ref.Data,2005,34:553

34 Glendening,E.D.;Weinhold,F.J.Comput.Chem.,1998,19:610

Density Functional Theory Study on N—O Bond Dissociation Enthalpies

ZHENG Wen-Rui*XU Jing-Li*XIONG Rui
(College of Chemistry and Chemical Engineering,Shanghai University of Engineering Science,Shanghai201620,P.R.China)

A number of density functional theory(DFT)methods were compared for the calculation of N—O bond dissociation enthalpies(BDEs)with the experimental values on the basis of the high-precision calculation methods G3 and G3B3.We found that the B3P86 method gave the lowest root of mean square error of 6.36 kJ·mol-1for calculating N—O BDE of 15 molecules and the correlation coefficient between the theoretical and experimental values was 0.991. We,therefore,used this method to calculate the N—O BDEs of non-aromatic and aromatic compounds.Using natural bond orbital analysis,quantitative relationships between some N—O BDEs and the corresponding N—O bond lengths, atomic charges,bond orders were determined.In addition,we predicted the N—O BDEs of several typical heterocyclic aromatic compounds using the B3P86 method.

Density functional theory; Bond dissociation enthalpy; Natural bond orbital analysis; N—O bond

O641

Received:May 4,2010;Revised:June 1,2010;Published on Web:July 22,2010.

*Corresponding authors.ZHENG Wen-Rui,Email:wrzheng@sues.edu.cn;Tel:+86-21-67791216;Fax:+86-21-67791220.

XU Jing-Li,Email:xujingli@sues.edu.cn;Tel:+86-21-67791220.

The project was supported by the Foundation of Shanghai Excellent Youth(B-8500-08-0110),School Start-Up Fund(08-22)and Innovation Fund (cx0904009),China.

上海优青科研基金(B-8500-08-0110),校启基金(08-22)和创新项目基金(cx0904009)资助项目

ⒸEditorial office of Acta Physico-Chimica Sinica