流体力学半径对估算胶体微球聚集速率常数的影响

杜 嬛 徐升华 孙祉伟 阿 燕

(中国科学院微重力重点实验室,中国科学院力学研究所,北京 100190)

流体力学半径对估算胶体微球聚集速率常数的影响

杜 嬛 徐升华 孙祉伟*阿 燕

(中国科学院微重力重点实验室,中国科学院力学研究所,北京 100190)

胶体粒子聚集速率常数实验值远低于理论值一直是被普遍关注的问题.聚集速率常数的理论推导是基于粒子的几何半径来考虑的,但决定粒子扩散速率及聚集速率的应该是粒子的流体力学半径(大于几何半径),因而它是使聚集速率常数实验值低于理论值的因素之一.影响流体力学半径的因素很多,其中,带电粒子在溶液中因表面存在双电层,会明显增大流体力学半径,造成聚集速率减慢.而双电层的厚度又随溶液中离子强度的不同而改变.本工作在聚集速率的公式中引入了修正因子,即几何半径与其流体力学半径之比,以修正由于用几何半径代替流体力学半径带来的误差.其中几何半径和流体力学半径可以分别用扫描电镜(SEM)和动态光散射(DLS)来测定.以两种粒径的聚苯乙烯带电微球为例,考察了在不同离子强度下,该误差的大小.结果发现,对于半径为30 nm的微球,用流体力学半径计算的慢聚集速率常数比理论值偏低约8%.该误差随离子强度增加而减少.对于快聚集情况,流体力学半径对聚集速率基本没有影响.

聚苯乙烯微球; 离子强度; 流体力学半径; 几何半径; 聚集速率常数

胶体悬浮粒子体系的稳定性和聚集动力学方面的研究对化工材料、医药、环境工程、纳米科学等方面都有重要的理论和实践意义[1-6].胶体分散体系的性质,如光学、电学、力学和流体力学等都与其稳定性密切相关.当胶体体系由分散状态转化为聚集状态时,几乎所有的胶体性质都会发生相应变化,所以胶体的稳定性就成为胶体科学的核心问题之一.

早在1917年Smoluchowski[7]就导出了由布朗运动碰撞引起的快聚集的理论公式[8-9].此后,人们对聚集过程的认识,在近一个世纪的发展中基本是沿着这一思路展开的.然而,迄今为止很多研究结果[10-11]表明,对于快聚集来说,其聚集速率常数的实验值远低于根据Smoluchowski的理论计算得到的结果(实验值一般只有理论值的40%-60%[11]).对此,各国研究人员从不同角度进行了解释.其中一些研究者怀疑是重力的影响造成的聚集减慢[12-14].欧空局科学家Folkersma等[12-13,15]利用密度匹配法及探空火箭创造的微重力条件,对直径为2 μm的聚苯乙烯微球的聚集行为进行了一系列实验,并在国际上多种学术刊物上发表了他们所得到的实验和相应的理论估算结果.其引人注目的结论是:在微重力条件下聚集速率要比地面条件下快10多倍.根据他们的结果,重力引起的对流及沉降分别可以造成聚集速率的减慢，达到420%和270%.Folkersma等[12]根据其浊度法测量的结果计算所得到的绝对快聚集速率常数值显示,绝对快聚集的速率常数的值在微重力条件下才非常接近于理论值.他们认为其微重力实验结果似乎解释了聚集速率实验值远低于理论值的谜团.Sun等[16-27]针对他们的结果从不同角度进行了验证,认定Folkersma的结论站不住脚,实验存在严重问题.例如,当用重水代替水时,其粘度会有25%的增加,必须对密度匹配实验的结果进行相应的修正,他们却没有做.特别是在用浊度法测量绝对聚集速率常数时,他们所用的公式远不适用于直径为2 μm这么大的粒子[21],因而他们的结果和结论是不可靠的.

除了重力因素外,粒子间的流体动力学相互作用也是目前普遍认为使聚集速率常数实验值低于理论值的原因[28-32].在Smoluchowski的理论假设中,扩散系数被视为常数.然而,当两粒子互相靠近时,粒子间的流体会阻碍它们的接近,而且越接近这种阻力越大,即扩散系数并不是固定不变的.我们研究组用计算机模拟已证实引入这种流体动力学作用后,快聚集速率会比不考虑该作用时的下降35%以上[26].所以流体动力学作用可以在相当大程度上解释速率常数实验值低于理论值的事实.

除了重力和流体动力学作用之外还有一些可能影响扩散速率的因素,其中很重要的就是粒子的半径如何定义.在Smoluchowski理论公式的推导过程中,是将粒子的半径作为不变的几何半径来考虑的.这样,当粒子增大时,扩散速率减慢,但两次碰撞间需行走的距离同时缩短,两个效应相互抵消.因此其聚集速率常数的公式中并没有半径出现.但是,当粒子在流体介质中运动时,会带动一部分流体与其一起运动,扩散就会减慢,相当于半径变大了.即从流体力学角度来看,其起作用的半径要比几何半径大.这个半径通常称之为“流体力学半径”.影响聚集速率的关键因素是扩散速度,所以从粒子真实的扩散角度来看,必须采用“流体力学半径”而不是几何半径.因此,从这点来说,实验的聚集速率必然比理论值低.影响流体力学半径的因素很多,比如,粒子的材料,表面特性、溶剂的组分以及溶液中的离子强度等因素都会对流体力学半径的大小产生影响.特别重要的情况是带电粒子.因为它们会吸引溶液中一部分带相反电性的离子,形成双电层结构.粒子运动时会带动一部分溶液分子,使得流体力学半径变大.当溶液的离子浓度升高时,双电层被压缩,流体力学半径变小,扩散变快,聚集速率就会提高.本研究的侧重点就是考察当用流体力学半径代替几何半径估算聚集速率常数时会有多大区别.在不同粒径和不同离子浓度条件下其影响的程度有何变化.

1 理论背景

聚集过程基本分为两种:由扩散限制的聚集(DLA),即快聚集;由反应限制的聚集(RLA),也就是慢聚集.对于快聚集体系,粒子之间只要发生碰撞就会聚集.因此,可以从粒子扩散的角度来得到聚集速率.Smoluchowski的分析就从理论上推导得出了快聚集情况下聚集速率常数的值.在理论分析中,首先考虑其它粒子能与粒子发生碰撞的流通通量.通过分析可得到,当固定一个粒子j时,第i种类型的粒子能与粒子j发生碰撞的流通通量表达式为

其中,ni为第i种粒子的浓度;Rij为两个粒子发生碰撞时它们之间的距离,对于单分散体系,Rij即是粒子的直径;Di为粒子i的扩散系数.考虑到粒子j实际上也是可以运动的,因此需将式(1)中的Di用它们的相对扩散系数Dij替代,实际上也即是Di的两倍.这样单位时间内单位体积中粒子的碰撞次数为

同样地,对于单分散的情况,ni=nj.对于快聚集情况,每次碰撞都会导致粒子聚集,因此,可推导出i、j粒子的快聚集速率常数:

悬浮液中,球形粒子的扩散系数Di是由Stokes-Einstein公式得到:

式中k为Boltzmann常数,T为绝对温度,μ为溶液的粘度,r为半径.这里的r实际上应该是与Stokes-Einstein公式对应的流体力学半径[33-34],但在Smoluchowski的推导中,这里的r取的是粒子本身的实际半径或几何半径.这样从公式(3)可以得到聚集速率常数的值为

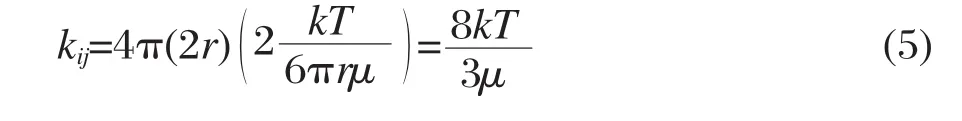
这就是Smoluchowski的快聚集速率理论值,与粒径无关.然而,实际公式(4)中的r应当为粒子在流体中扩散时表现出来的半径,即前面说的流体力学半径,它的数值可能与粒子的真实半径有所不同.如果用rr指代真实半径,用rf指代流体力学半径,则从公式(3)可以得到:

以上推导针对快聚集体系.对于慢聚集体系,粒子发生碰撞后需要越过排斥势垒才会发生聚集.如果不考虑流体力学半径的影响,慢聚集速率可表示为

其中,W为体系的稳定率.在理论分析中,它可以由粒子间的相互作用势能来表达出来.类似地,如果要考虑流体力学半径的影响,公式(8)需变为

因此,由式(7)和(10)可以看出,无论是慢聚集体系还是快聚集体系,流体力学半径对聚集速率的影响是类似的.通过式(7)和(10)计算出的聚集速率常数校正因子,可以反应胶体粒子的流体力学半径对其聚集速率常数的影响程度.因为流体力学半径一般比几何半径大,校正因子小于1.只有当几何半径和流体力学半径相等时,才有校正因子α=1的结果.

2 实验部分

前面讨论过,聚集速率的理论公式采用的是粒子的几何半径,而决定粒子扩散快慢的是流体力学半径.这是聚集速率的实验值低于理论值的原因之一.如果能够得到前部分引入的校正因子,就可以估计其影响程度.本工作就是以带电聚苯乙烯(PS)胶乳球为例,通过测定在不同离子强度下的几何半径和流体力学半径,确定校正因子.考察在不同粒径和离子强度条件下,采用几何半径代替流体力学半径对聚集速率常数的影响程度.几何半径的测量是利用扫描电镜(SEM)完成的,因为这种测量方法提供的是真实的几何半径值.而粒子在溶液中的流体力学半径是采用动态光散射法(DLS)得到的.DLS也称光子相关谱(PCS)或准弹性光散射,测量的是光强的波动随时间的变化.在DLS中,通过检测溶液中颗粒散射光的强度起伏能够获得胶体颗粒在做布朗运动时的扩散系数,再根据Stokes-Einstein公式便可算出粒子的流体力学半径.

2.1 试 剂

苯乙烯(St)、过硫酸钾(KPS)、碳酸氢钠(NaHCO3)、苯乙烯磺酸钠(NaSS)、氯化钠(NaCl)均为分析纯,国药集团化学试剂有限公司生产;St用前减压蒸馏除去阻聚剂,KPS用水重结晶提纯;实验用水为二次蒸馏水.

2.2 聚苯乙烯微球

本实验中采用了两种PS微球,一种是由美国Duke公司提供的直径约60 nm的PS标准微球,记为PS60.另一种是自行制备的直径约为200 nm的PS微球,记为PS200.

在PS200制备过程中,在带有冷凝管、温度计、机械搅拌器的500 mL玻璃反应釜中预先通氮除氧,然后将一定比例的二次蒸馏水、St、NaHCO3、NaSS加入其中,氮气保护,待体系温度达到75℃后加入KPS水溶液,并在此温度下持续反应24 h.反应停止后,冷却至室温,经多次离心、洗涤以去除溶液中残留的引发剂残基和未反应的单体及电解质,至离心后上清液的电导率接近纯水的电导率,得到PS胶体微球.

2.3 测试仪器

用JSM-6700F型(日本)扫描电子显微镜测定PS微球的几何直径,样品表面进行喷金处理,金厚度约为3-5 nm.用SEM测量100个微球粒径,按下面公式计算微球粒径的标准偏差δ和分散系数ε.

式(11-12)中Di为单个粒子的直径;D为粒子的平均直径;n为粒子数目.粒径单分散性用体均粒径与数均粒径之比(DV/Dn)表示,一般将DV/Dn＜1.05作为粒子单分散的标志[35].

用Brookhaven公司生产的90plus动态/静态激光光散射仪测定样品的流体力学直径.在光散射实验中,试样的温度都通过恒温水浴控制在25℃,散射角为90°.实验中可以通过程序控制实验循环次数、间隔时间和持续时间.在每个实验中,设置了100次测定,每次持续时间30 s,间隔时间为0 s,最后流体力学直径的结果为对这100个数据取平均值.

2.4 PS胶体溶液的制备及表征

分别取一定量的两种粒径大小的PS微球,加纯水(Millipore milli-Q system,电导率为18.2 MΩ· cm)稀释至体积浓度为0.002%,采用动态/静态激光光散射仪测定样品的流体力学直径.PS球都是在比较低的离子强度下保存的.加入适量的NaCl可改变离子强度.然后用动态/静态激光光散射仪测定不同NaCl浓度下胶体粒子的流体力学直径.

3 结果与讨论

3.1 胶体颗粒几何半径的表征结果

图1为不同粒径大小的单分散的聚苯乙烯微球的SEM照片.由图1可以看出,外购的和自制的PS微球都具有良好的球形度,表面光滑且分布均匀.对 PS微球几何半径的统计计算结果示于表1.由表1可见,两种不同粒径的PS微球的平均偏差和分散系数小,颗粒的单分散性好.

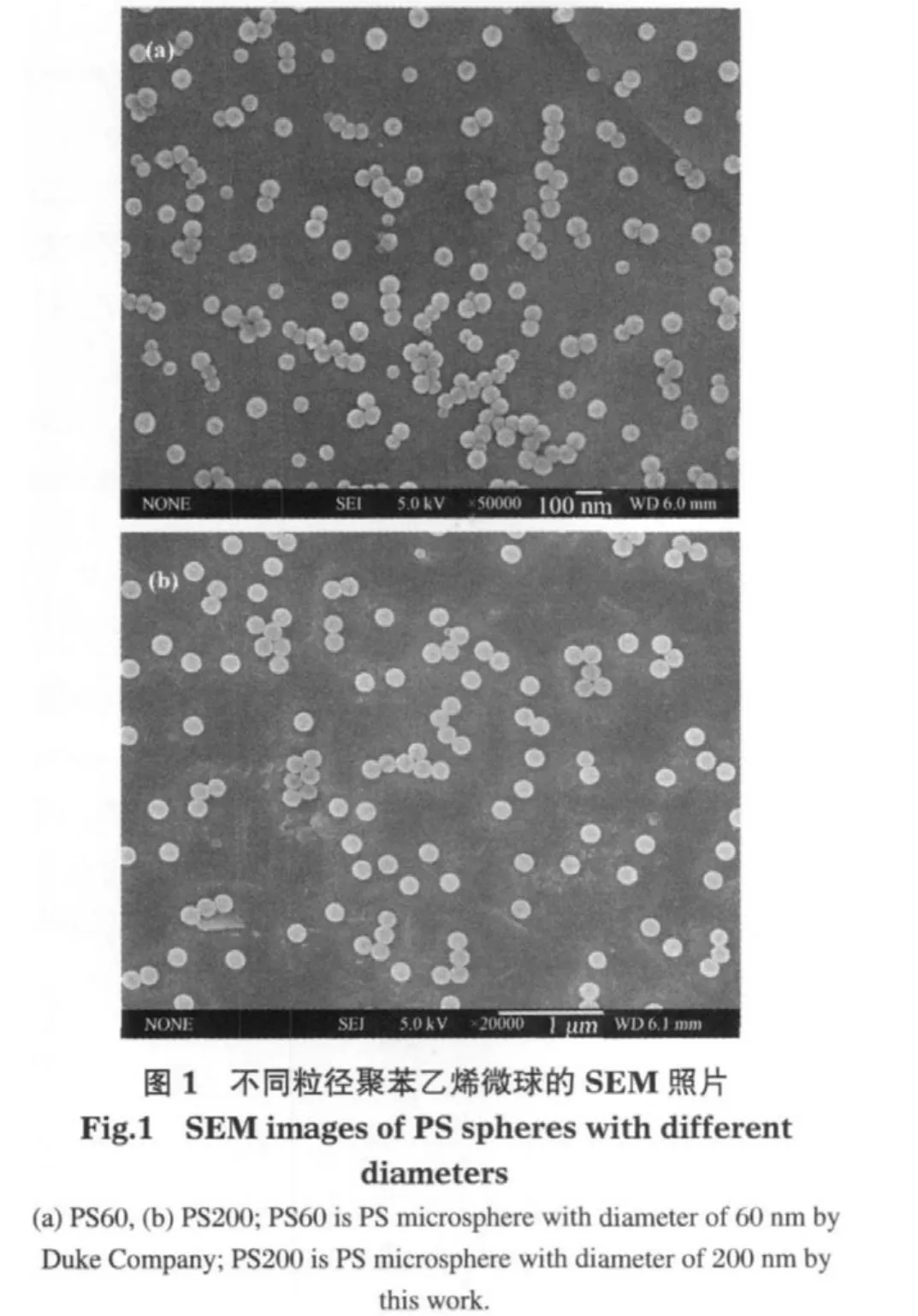
3.2 DLS法对胶体颗粒流体力学半径的表征结果

图2是两种粒径大小PS微球流体力学半径(包括测量值的误差范围)在不同NaCl浓度条件下的变化曲线.当NaCl浓度为1×10-7mol·L-1时,表示纯水中PS微球的流体力学半径.从流体力学半径随盐浓度的变化趋势可见,纯水稀胶体体系中的PS微球表面的双电层厚度最大,因而粒子的流体力学半径大于其实际几何半径.当胶体溶液的离子强度逐渐提高,即向溶液中添加一定浓度的盐时,由于体系中的离子大大压缩了双电层厚度,使粒子的流体力学半径大小逐渐接近于其几何半径.

表1 聚苯乙烯微球几何半径统计结果Table 1 Statistical results of the PS spheres geometric radius

由图2可见,随着盐浓度的增加,不同大小的粒子的流体力学半径均不断减小.当NaCl浓度较低时(≤1×10-5mol·L-1),与纯水中的PS微球相比,其流体力学半径的减小幅度不太明显.当NaCl浓度由1×10-5mol·L-1继续增大时,PS微球的流体力学半径明显减小.当盐浓度达到1×10-2mol·L-1时,其流体力学半径已经非常接近于利用SEM所测量的粒子实际半径.当盐浓度进一步增大时,体系中的粒子将会很快发生聚集.在这种情况下,利用DLS法测量的结果将是一些聚集体的平均流体力学半径,而不是单个粒子的流体力学半径.因此在本实验中,添加的最大盐浓度为1×10-2mol·L-1.这是因为在1×10-2mol·L-1的盐浓度附近,粒子的流体力学半径随着盐浓度的变化已经非常缓慢,基本上趋向于一个定值.这个值又很接近粒子实际半径.因此可以推断,当盐浓度继续增大时,单个粒子的流体力学半径将基本上等于粒子实际半径或几何半径.这对于我们如何正确应用DLS法测量粒径也是一个很好的提示,即适当提高离子强度才能得到正确的结果,太低会偏离真实粒径太远,太高又会造成聚集.

由于PS微球表面的双电层能够造成其流体力学半径与实际的几何半径存在一定程度的差别,故可能会对聚集速率的理论分析产生影响.因此在本实验的基础上,将进一步对采用粒子几何半径和流体力学半径对聚集速率常数上造成的差别进行研究对比,考察流体力学半径对聚集速率常数的影响程度.

3.3 流体力学半径对聚集速率常数的影响

将图2中的实验数据分别代入式(7)和(10),可以清楚地观察到胶体粒子的流体力学半径对其聚集速率常数的影响情况,结果如图3所示.由图3可见,当盐浓度小于1×10-2mol·L-1时,实验测得的两种不同粒径大小的PS微球的聚集速率常数均低于理论推导得出的聚集速率常数.纯水中PS微球的流体力学半径对聚集速率的影响最大:样品PS60和PS200的聚集速率常数的修正值分别约为92%和96%,也就是聚集速率常数实验值只是理论值的92%和96%.随着胶体溶液中盐浓度的逐渐增大,在误差范围之内，两个样品的校正因子值逐渐接近于1,表明胶体粒子的聚集速率常数越接近于理论值.这说明,对于快聚集体系,由于盐浓度较高,流体力学半径接近于实际半径,因此不考虑流体力学半径的修正.而对于慢聚集体系,特别是盐浓度较低的情况,在分析其聚集速率时需要对流体力学半径的影响进行修正.另外,由图3还可见,与样品PS200相比,离子强度相同时,流体力学半径对PS60的聚集速率的影响更大.这是因为当材料和介质固定时,粒子表面的双电层厚度相对小粒子来说更大.因此,颗粒粒径越小,其流体力学半径的影响越明显.

4 结 论

以半径分别约为30和100 nm的聚苯乙烯带电微球为例,研究了在不同离子强度下,用几何半径代替流体力学半径会造成的聚集速率常数的误差.为了定量的估计该误差的大小,我们在聚集速率常数的理论公式中引入了修正因子.几何半径和流体力学半径可以分别用SEM和DLS来测定.结果表明,对于慢聚集,半径约为30和100 nm的PS微球修正后的聚集速率常数分别约是原来理论值的92%和96%.用几何半径代替流体力学半径造成的误差随离子强度的升高而减低.对于快聚集情况,流体力学半径对聚集速率基本没有影响.本研究表明,在粒子聚集速率的理论分析中,需要考虑流体力学半径的影响并修正理论分析的公式,特别是对于慢聚集过程以及粒径比较小的情况,这一结果也为完善分散物质聚集动力学的理论模型提供条件,同时对深化与聚集行为相关的应用基础也有积极意义.此外,我们的结果对正确使用DLS法测量粒径也有很好的借鉴作用.适当提高离子强度才能得到正确的结果,太低会偏离真实粒径太远,太高又会造成粒子聚集.

1 Wang,G.T.Colloidal stability.Beijing:Science Press,1990:1-2 [王果庭.胶体稳定性.北京:科学出版社,1990:1-2]

2 Jiang,Z.B.Science Information,2006,11:12 [姜兆波.科技信息,2006,11:12]

3 Hu,Q.Y.;Lan,Y.Q.;Xue,J.H.Soilds,1996,28:290 [胡琼英,兰叶青,薛家骅.土壤,1996,28:290]

4 Fan,X.;Guo,Z.R.;Hong,J.M.;Zhang,Y.;Zhang,J.N.;Gu,N. Nanotechnology,2010,21:105602

5 Yue,L.;Tao,S.L.;Zhang,X.H.;Wu,S.K.Journal of Functional Polymers,2005,18:248 [岳 玲,陶斯禄,张晓宏,吴世康.功能高分子学报,2005,18:248]

6 Zhang,S.F.;Sun,L.L.;Xu,J.B.;Zhou,H.;Wen,H.Acta Phys.-Chim.Sin.,2010,26:57 [张胜飞,孙丽丽,徐俊波,周 涵,温 浩.物理化学学报,2010,26:57]

7 Smoluchowski,M.Z.Phys.Chem.,1917,92:129

8 Elimelech,M.;Gregory,J.;Jia,X.;Williams,R.A.Particle deposition and aggregation measurement,modelling and simulation.Amsterdam:Elsevier,1995

9 Kruyt,R.H.Colloid science,Vol.1.Irreversible systems. Amsterdam:Elsevier,1952

10 Adachi,Y.Adv.Colloid Interface Sci.,1995,56:1

11 Fukasawa,T.;Adachi,Y.J.Colloid Interface Sci.,2006,304:115

12 Folkersma,R.;Van Diemen,A.J.;Stein,H.N.J.Colloid Interface Sci.,1998,206:482

13 Folkersma,R.;Stein,H.N.J.Colloid Interface Sci.,1998,206: 494

14 Folkersma,R.;Van Diemen,A.J.;Stein,H.N.Adv.Colloid Interface Sci.,1999,83:71

15 Krutzer,L.L.M.;Folkersma,R.;Van Diemen,A.J.;Stein,H.N. Adv.Colloid Interface Sci.,1993,46:59

16 Sun,Z.W.;Qiao,R.L.J.Colloid Interface Sci.,2000,223:126

17 Sun,Z.W.;Li,Y.M.;Xu,S.H.;Lou,L.R.;Dai,G.L.;Dong,X. Q.J.Colloid Interface Sci.,2001,242:158

18 Sun,Z.W.;Chen,Z.Y.Chin.Phys.Lett.,2003,20:1634

19 Liu,J.;Sun,Z.W.;AA,Y.Chin.Phys.Lett.,2005,22:3199

20 Xu,S.H.;Liu,J.;Sun,Z.W.J.Colloid Interface Sci.,2006,304: 107

21 Sun,Z.W.;Liu,J.;Xu,S.H.Langmuir,2006,22:4946

22 Sun,Z.W.;Xu,S.H.;Liu,J.;Li,Y.M.;Lou,L.R.;Xie,J.C. J.Chem.Phys.,2005,122:184904

23 Sun,Z.W.;Xu,S.H.;Dai,G.L.;Li,Y.M.;Lou,L.R.;Liu,Q.S.; Zhu,R.Z.J.Chem.Phys.,2003,119:2399

24 Sun,Z.W.;Liu,J.;Xu,S.H.Chin.Phys.Lett.,2005,21:2119

25 Li,X.;Xu,S.H.;Sun,Z.W.Acta Phys.-Chim.Sin.,2009,25:207 [李 旭,徐升华,孙祉伟.物理化学学报,2009,25:207]

26 Li,X.;Xu,S.H.;Sun,Z.W.Acta Phys.-Chim.Sin.,2009,25: 2130 [李 旭,徐升华,孙祉伟.物理化学学报,2009,25:2130]

27 Liu,J.;Xu,S.H.;Sun,Z.W.Langmuir,2007,23:11451

28 Honig,E.P.;Roebersen,G.J.;Wiersema,P.H.J.Colloid Interface Sci.,1971,36:97

29 Happel,J.;Brenner,H.Low reynolds number hydrodynamics. Dordrecht:Kluwer,1991

30 Batchelor,G.K.J.Fluid Mech.,1976,74:1

31 Crocker,J.C.J.Chem.Phys.,1997,106:2837

32 Bhattacharya,S.;Blawzdziewicz,J.;Wajnryb,E.J.Fluid Mech., 2005,541:263

33 Kätzel,U.;Vorbau,M.;Stintz,M.;Gaudig,T.G.;Barthel,H.Part. Part.Syst.Charact.,2008,25:19

34 Zhang,Y.B.;Qi,W.;Su,R.X.;Yuan,S.X.;Jin,F.M.;He,Z.M. Chin.J.Anal.Chem.,2007,35:809[章宇斌,齐 崴,苏荣欣,袁素霞,靳凤民,何志敏.分析化学,2007,35:809]

35 Goodwin,J.W.;Hearn,J.;Ho,C.C.;Orrewill,R.H.Brit.Polym. J.,1973,5:347

Effect of the Hydrodynamic Radius of Colloid Microspheres on the Estimation of the Coagulation Rate Constant

DU Xuan XU Sheng-Hua SUN Zhi-Wei*AA Yan
(Key Laboratory of Microgravity,Institute of Mechanics,Chinese Academy of Sciences,Beijing 100190,P.R.China)

Experimental values of the coagulation rate constant for colloidal particles are known to be much lower than the theoretical values.Only the particle′s geometric radii are used in the theoretical derivation of coagulation rate constant.However,it should actually be the hydrodynamic radius(larger than the geometric radius)that determines the particles′diffusion speed and thus the coagulation rate.Therefore,it is one of the reasons that cause the experimental coagulation rate constant lower than the theoretical one.Many factors affect the hydrodynamic radius and among them the electric double layer can significantly swell the hydrodynamic radius,which lowers the coagulation rate.The thickness of the electric double layer changes with the ionic strength of the solution.To correct the error caused by neglecting the difference between the geometric and hydrodynamic radius,a correction factor,which is the ratio of geometric radius to hydrodynamic radius,is introduced in this study.The geometric radius and the hydrodynamic radius were determined by scanning electron microscopy(SEM)and dynamic light scattering(DLS),respectively.Two different sized polystyrene microspheres were used to investigate the effect of ionic strength on the difference between the experimental coagulation rates and the theoretical ones.The results show that for slow aggregation,the rate constant calculated by using the hydrodynamic radius can be lower than its theoretical value by about 8%for microspheres with radius of 30 nm.This difference decreases with the increase of ionic strength.The effect of the hydrodynamic radius on the coagulation rate is negligible for fast aggregation.

Polystyrene microspheres; Ionic strength; Hydrodynamics radius; Geometric radius; Coagulation rate constant

O648

Received:April 2,2010;Revised:May 19,2010;Published on Web:August 17,2010.

*Corresponding author.Email:sunzw@imech.ac.cn;Tel:+86-10-82544093.

The project was supported by the National Natural Science Foundation of China(10972217,10932012)and Knowledge Innovation Program of the Chinese Academy of Sciences(KJCX2-YW-L08).

国家自然科学基金(10972217,10932012)和中国科学院知识创新工程(KJCX2-YW-L08)资助项目

ⒸEditorial office of Acta Physico-Chimica Sinica