基于相位相关的亚像素配准技术及其在电子稳像中的应用
孙 辉,李志强,孙丽娜,郎小龙
(中国科学院长春光学精密机械与物理研究所,吉林长春 130033)
1 引 言
图像配准是一种基于傅里叶功率谱的频域相关技术,是由 Kuglin和 Hines在 1975年提出来的[1]。近几十年来,广大专家学者在图像配准方面做了深入的探索和研究,在优化算法、提高配准精度等方面提出了许多行之有效的方法。在各种图像配准方法中,基于相位相关的配准方法以其算法简单易行、运算量小、配准精度高等优点在学术界受到极大关注,在医学图像处理、遥感图像处理、计算机视觉、运动分析、工业检测等领域得到了广泛应用。
图像配准可以将来自不同时间、不同角度或不同数据源的几幅图像对准,一般可实现像素级配准精度,满足实际应用要求。尽管如此,在很多应用领域,为提取更准确的图像信息,通常需要亚像素级的配准精度。文献[2]提出了一种扩展的相位相关法,即在相位相关法基础上,通过理论分析将其扩展到亚像素级配准精度。由于该方法只提取互功率谱中的相位信息,减少了对图像内容的依赖,具有较强的抗干扰能力,是目前广泛使用的频域配准方法[3~10]。
本文针对序列图像中的图像失稳问题,将基于扩展的相位相关图像配准技术用于检测视频图像帧间亚像素级的运动量,然后对图像进行亚像素级的运动补偿,输出平滑、稳定的视频图像。与像素级的运动检测和补偿相比,本文方法可实现更高的稳定精度,有效提高了图像补偿质量。
2 亚像素配准技术
2.1 相位相关配准原理
设f1(x,y)为基准图像,f2(x,y)为f1(x,y)平移(x0,y0)后的位移图像,两者满足如下关系:
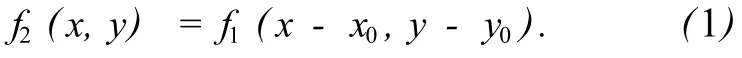
对式 (1)做傅里叶变换,有:
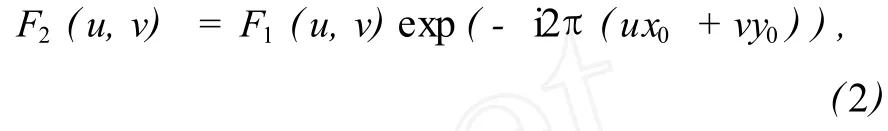
式中F1(u,v)和F2(u,v)分别表示f1(x,y)和f2(x,y)的傅里叶变换。
因此,两幅图像之间归一化的交叉功率谱可表示为:
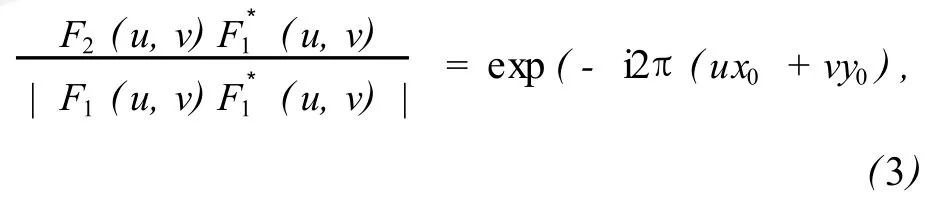
式中*表示复共轭,将式 (3)两端进行傅里叶逆变换,可得相位相关函数如下:
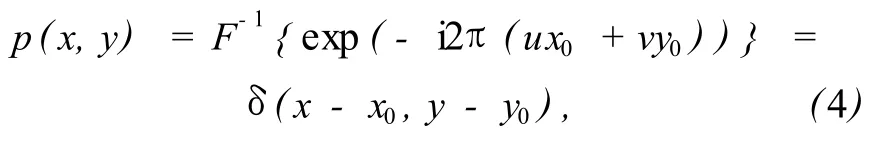
式中δ(x-x0,y-y0)为典型的 Dirac函数,也称冲激函数,该函数在中心点(x0,y0)处不为零,在其它位置均为零。图1显示了相位相关函数曲线,其中图1(a)显示了位移等于 0像素的相关曲线,图1(b)显示了在水平方向产生 0.5像素位移情况下的相关曲线。
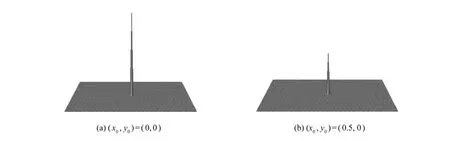
图1 相位相关函数 p(x,y)Fig.1 3D plots of phase correlation functionp(x,y)
在实际应用时,由于傅里叶变换对f(x,y)的周期性有要求,而实际图像一般都不具备周期特性,所以为减小边缘效应对配准精度的影响,需采用加窗技术,即对输入图像进行适当加权处理,使其具有周期性特征,以符合傅里叶变换条件。
典型的 2D Hanning窗定义如下:

将上述形式的加窗函数作为加权系数,分别作用于f2(x,y)和f1(x,y)并进行傅里叶变换,可较好地减小边缘效应。
2.2 亚像素精度检测
常规的频域相关配准算法只能检测到像素级的平移运动量,为获取亚像素级运动量,本文采用基于最小二乘法的二次曲面拟合方法,通过在相关峰值坐标点附近用曲面拟合相位相关值,拟合曲面的峰值坐标即为平移运动参数。
根据上述分析,本文选择如下拟合函数:
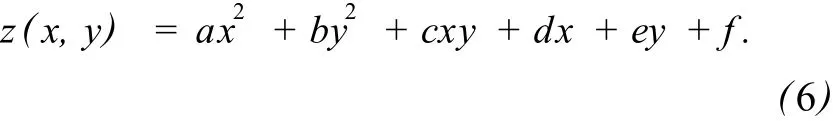
拟合函数z(x,y)的系数可通过解下列方程解出:

式中:

采用最小二乘法求解方程,即可解出拟合函数的系数。
为此,在式 (6)中分别对x,y求偏导,并使偏导为 0,即:
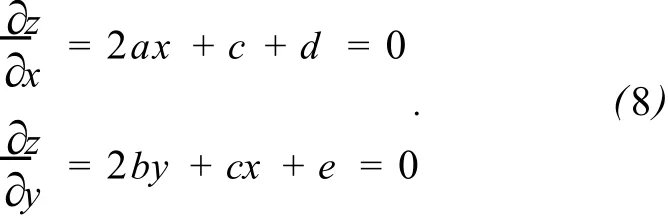
由式 (8)可解得:
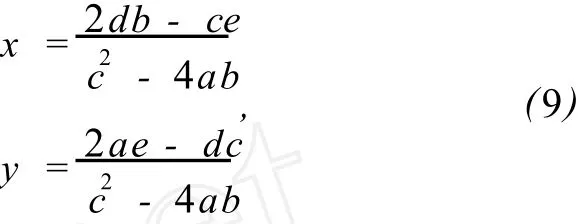
式中的x,y即为所求的平移量且具有亚像级的分辨率。
2.3 亚像素补偿
序列图像运动补偿是根据图像运动矢量,对图像像素位置进行重组实现的。通常,图像之间的运动包括平移运动、旋转运动、尺度变换及仿射变换等,本文只讨论平移运动情况。在平移运动中,两幅图像只有水平和垂直方向的运动变化,按照运动方向等量反向移动图像即可实现运动补偿。
设位移图像g(x,y)通过运动补偿得到结果图像f(x,y),则f(x,y)和g(x,y)建立一一对应关系 ,即:
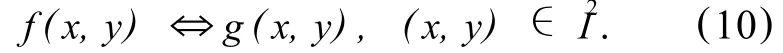
当平移量为亚像素时,(dx,dy)∈R2,图像平移运动补偿公式如下:
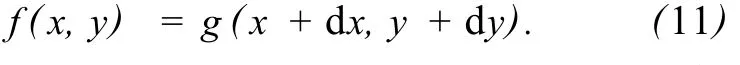
采用式 (11)进行图像补偿,对于f(x,y)的每一个像素坐标(x,y),都可以保证在g(x,y)中有一个对应的像素点坐标 (x+dx,y+dy)。由于x+dx和y+dy是小数,而g(x,y)图像坐标是整数,所以在补偿图像时,不能简单地进行整数坐标映射,要根据平移运动量进行适当的平滑处理,否则在小数转化为整数的过程中将产生误差,影响图像补偿精度。
为了提高补偿质量,采用双线性插值方法对图像像素灰度值进行了平滑处理,根据位移图像坐标 (x+dx,y+dy)与四邻域位置及灰度值的对应关系,通过四邻域灰度值加权平均的方法计算f(x,y)的像素灰度值。
双线性插值公式如下:

式中i,Δx分别表示x+dx的整数部分和小数部分,j,Δy分别表示y+dy的整数部分和小数部分 ,即 Δx=x+dx-i,Δy=y+dy-j。采用双线性插值处理后的图像边缘清晰、完整、无锯齿,具有较好的补偿效果。
3 仿真实验结果
为检测亚像素检测精度及稳像效果,在实验室进行了仿真实验。
样本图像选用标准样本图像库中的 bridge图像,原始图像见图2(a),对比图像通过对原始图像进行平移得到。为检测本文方法对亚像素运动量的检测精度,研究人员在水平和垂直方向上同时对原始图像进行步长为 0.01 pixel的平移操作,一共生成 50帧对比图像,其中第一帧位移dx=dy=0.01 pixel,第 50帧位移 dx=dy=0.5 pixel,如图1(b)、图1(c)所示。图像位移曲线见图3。

图2 样本图像Fig.2 Sampling images
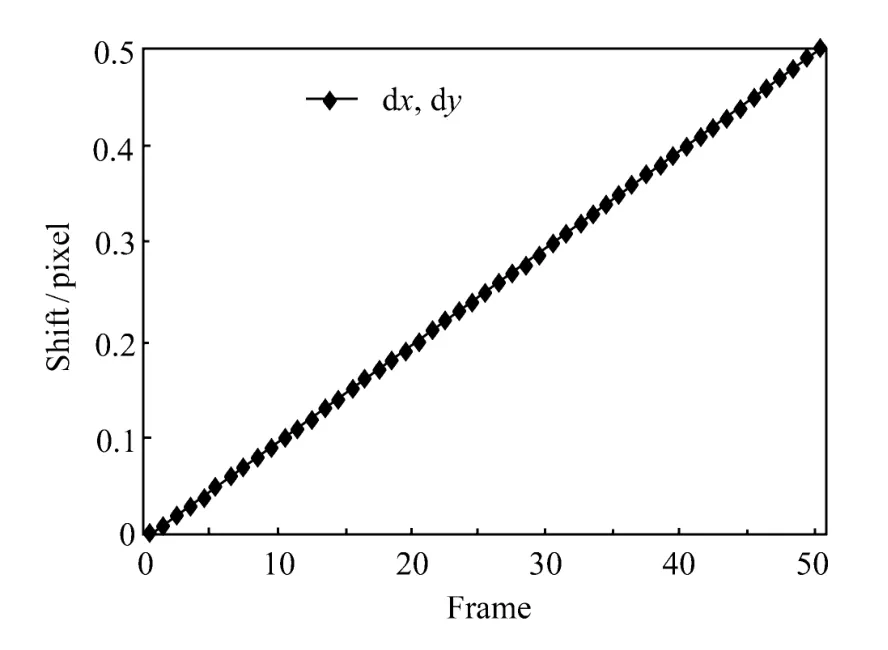
图3 亚像素位移曲线Fig.3 Curve of sub-pixel displacement
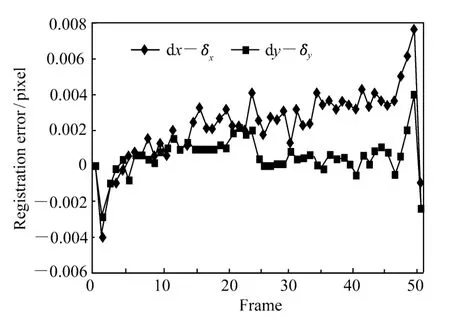
图4 运动量检测误差曲线Fig.4 Errors in displacement estimation
采用本文介绍的图像配准算法对样本图像进行运动量检测,计算从第 1帧到第 50帧对比图像相对原始图像的亚像素级的运动矢量 (δx,δy),由于每幅对比图像相对参考图像的真实位移量已知,可以统计配准结果与真实位移量的误差,配准误差统计结果如图4所示。通过图4中的误差曲线可以看出,在 50个位移矢量检测结果中,与真实位移量的最大误差仅为 0.008 pixel。
采用上述亚像素运动量和式 (12)进行图像运动补偿,用均方根误差 (Root of Mean Square Error,RMSE)作为客观指标评价电子稳像效果,对 50帧样本图像分别统计补偿后的均方根误差值,统计结果见图5。从统计数据和误差曲线可以看出,补偿前最大误差为 12.8 pixel,经过亚像素级运动量检测和图像补偿后,最大误差仅为0.5 pixel,有效提高了图像补偿质量。
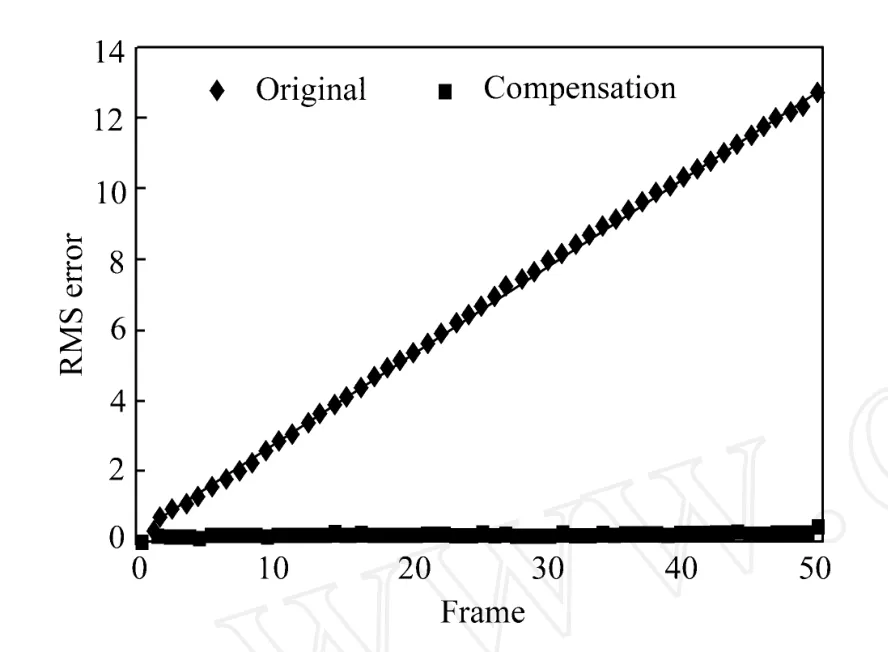
图5 图像补偿误差曲线Fig.5 RMS errors of compensation
4 结 论
本文介绍了基于相位相关的图像配准方法,并将该方法应用于视频序列图像的亚像素运动检测,通过双线性插值技术补偿亚像素运动量。实验结果表明,相位相关算法利用图像的互功率谱信息,减少了对图像内容的依赖,具有较强的抗噪能力;同时该算法具有亚像素级的配准精度,提高了图像运动的检测精度,通过亚像素图像补偿技术,可有效提高图像补偿质量和稳像效果。
[1] KUGL IN CD,H INESD C.The phase correlation image alignment method[A].Proc.Int.Conf.Cybernetics Society[C].San Francisco,USA,1975:163-165.
[2] FOROOSH H,ZERUB IA J,BERTHOD M.Extension of phase correlation to sub-pixel registration[J].IEEE Trans.Im age Processing,2002,11(3):188-200.
[3] 桂志国,韩焱.相位相关配准法及其在射线图像数字减影中的应用[J].仪器仪表学报,2004,25(4):520-522.GU I ZH G,HAN Y.Phase correlation technique for image registration and its application in dsa of radiographic image[J].Chinese J.Sci.Instrum.,2004,25(4):520-522.(in Chinese)
[4] 高世海,戴文刚,田仲.空域和频域相结合的景象匹配算法[J].中国图象图形学报,2000,5(A)(4):345-348.GAO SH H,DA IW G,T IAN ZH.Hybrid image registration algorithm of space domain and frequency domain[J].J.Im age Graphics,2000,5(A)(4):345-348.(in Chinese)
[5] 吴元昊,于前洋.基于傅里叶相位差的抗噪声位移估计算法[J].光学精密工程,2007,15(7):1137-1142.WU Y H,YU Q Y.Denoising algorithm of displacement estimation based on phase difference of Fourier transform[J].Opt.Precision Eng.,2007,15(7):1137-1142.(in Chinese)
[6] 冯林,管慧娟、藤弘飞.基于互信息的医学图像配准技术研究进展[J].生物医学工程学,2005,22(5):1078-1081.FENGL,GUAN H J,TENG H F.Advances in medical image registration based on mutual information[J].J.B iom edical Eng.Res.,2005,22(5):1078-1081.(in Chinese)
[7] 周永新,罗述谦.基于形状特征点最大互信息的医学图像配准 [J].计算机辅助设计与图形学学报,2002,14(7):654-658.ZHOU Y X,LUO SH Q.Medical image registration based on mutual infor mation of feature points[J].J.Com puter-A ided Design Com puter Graphice,2002,14(7):654-658.(in Chinese)
[8] 李治国,安锦文,赵银铃.基于相位相关的全局运动估计算法[J].计算机测量与控制,2008,16(4):532-534.L I ZH G,AN J W,ZHAO YL.Globalmotion est imation algorithm based on phase correlation[J].Com puterM easurem ent Control.,2008,16(4):532-534.(in Chinese)
[9] 黎俊,彭启民,范植华.亚像素级图像配准算法研究[J].中国图象图形学报,2008,13(11):2071-2075.L IJ,PENGQ M,FAN ZH H.Asurvey of sub-pixel image registration methods[J].J.Im age and Graphics,2008,13(11):2071-2075.(in Chinese)
[10] 徐宝昌,陈哲,赵龙.一种改进的最小二乘景象匹配算法[J].北京航空航天大学学报,2005,31(8):848-852.XU B CH,CHEN ZH,ZHAO L.Inproved least-squares acene matching algorithm[J].J.Beijing University Aeronautics and Astronautics,2005,31(8):848-852.(in Chinese)

