内建自测试的测试生成方法研究

郭斌

（山西省稷山广播电视服务中心，043200）

0 引言

内建自测试（Built-In-Self-Test，BIST）技术是可测性设计（Design for Test, DFT）的一种。内建自测试方法主要通过在芯片上集成测试结构完成测试图形的生成和测试响应的分析，这样在很大程度上缓解了对外部自动测试仪器（Automatic Test Equipment, ATE）的依赖，从而降低了测试成本[1-2]。

BIST的测试结构主要包括测试图形生成器（TPG）、输出响应分析器（ORA）和BIST控制单元（BCU），如图1所示。测试图形生成器（TPG）的一般结构包括存储有测试图形的ROM和线性反馈移位寄存器（LFSR）。测试响应分析器（ORA）的典型结构包括存有测试响应的压缩器和用LFSR组成的特征分析器（Signature Analyzer）。控制单元（BCU）用来控制测试和响应分析。

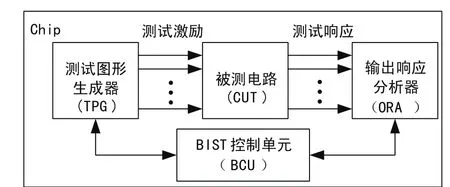
图1 典型内建自测试结构

内建自测试的优点主要体现在：

(1) 测试生成和测试响应分析都在片上进行，减少了测试对昂贵测试仪器的依赖性；

(2) 由于测试在片上进行，可以工作速度测试集成电路，因此缩短了测试时间，并且可以检测实际条件下的故障；

(3) 可以实现在系统经常性测试，这对可靠性要求较高的系统很有意义。

目前，对BIST研究主要集中在测试生成方法上，研究目标在于减小硬件开销，提高故障覆盖率，降低测试功耗和缩短测试时间等。本文即介绍了自BIST方法产生以来几种不同的测试生成方法，分析比较它们各自的特点，并讨论将来有待解决和改善的主要问题。

1 传统的测试生成方法

传统BIST的测试生成方法有穷举测试生成法、伪穷举测试生成法、伪随机测试生成法和确定性测试生成法等。

1.1 穷举测试生成法

穷举测试，顾名思义就是指测试图形包含了原始输入所有可能的排列组合，即所谓的穷举测试集。穷举测试的优点在于易生成测试向量和100%的故障覆盖率，但这样的方法只对小规模的纯组合电路有效。对于原始输入较多的电路来说，穷举测试所带来的测试时间是不可接受的[1]。而对于时序电路，穷举法并不适合，因为测试图形的时序对被测电路有非常大的影响。

1.2 伪穷举测试生成法

伪穷举测试通过对被测电路进行分块[3]，然后对每个分块电路进行穷举测试。这样既实现了每个分块电路的完全测试，又使得测试图形长度比穷举测试大大降低。但是这种方法在电路分块方面存在较大困难。

1.3 伪随机测试生成法

伪随机测试采用的测试图形具有随机特性。常用线性反馈移位寄存器（LFSR）来实现，这种方式产生的伪随机测试向量所需成本小。LFSR作为测试图形生成器生成测试向量已经成为内建自测试（BIST）中测试生成方法的主要结构。

伪随机测试既适用于组合电路测试，也适用于时序电路测试。但伪随机测试在可以接受的测试时间内不能得到足够的故障覆盖率。如果想提高故障覆盖率就必须增大测试图形的长度，但这同时也这大大增加了测试施加时间。

图2显示了故障覆盖率和测试图形长度的关系，从图中可以看出：随着伪随机测试码序列长度L的增加，故障覆盖率曲线接近饱和。所以随着故障覆盖率的提高，相同长度的伪随机测试码序列检测到的故障数越来越少，冗余伪随机测试码越来越多。这些冗余伪随机测试码检测不出任何故障，不仅不能提高故障覆盖率，而且会增加测试施加时间和测试功耗。

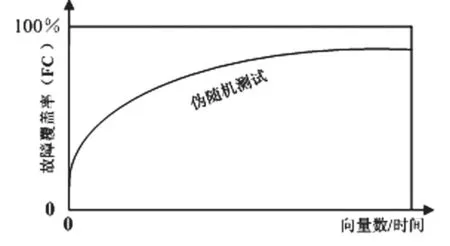
图2 伪随机测试故障覆盖率和测试向量数关系

1.4 确定性测试生成法

确定性测试是用专门的算法，如D算法、PODEM算法等，完成测试图形的生成，是对待定的故障类型生成测试图形。这是一个NP-complete问题，需要迭代法来加速生成过程。利用此方法生成的测试图形非常短，测试施加时间最短，但测试生成方法非常复杂，测试生成时间非常长。当和BIST相结合时，ATPG（Automatic Test Pattern Generation）生成的测试图形存储在ROM中。这种方法可以获得理想的故障覆盖率，但是测试开销太大，成本太高。

2 新兴的测试生成方法

传统的测试生成方法虽然结构简单，硬件开销小，但是这些方法都存在各种各样的问题，如测试施加时间比较长，故障覆盖率不高等。为了解决这些问题，如今主要从两个方面对测试生成方法进行改进：（1）修改被测电路；（2）修改测试图形生成器结构。修改被测电路结构可通过在电路中插入测试点，提高可观察点和可控制点的数目以实现少的测试图形获得高的测试覆盖率，但这种方法是以大的面积开销和性能损失为代价的。因此比较有效的方法是对以LFSR为基础的测试图形生长器结构进行适当修改。修改测试图形生成器结构比较常用的有两种方法：（1）加权测试。（2）混合测试生成法。

2.1 加权测试生成法

因为用LFSR产生的测试图形中每一位上0和1的概率基本相等，但为了用尽可能少的测试图形取得尽可能高的故障覆盖率，许多电路的测试图形中0和1的分布概率应不同。加权测试生成方法就是使得生成的测试图形具有不同的0和1的概率，可采用LFSR和组合逻辑电路构成，但这种方法需要存储数量较大的加权集，使得测试面积开销增大。

2.2 混合测试生成法

基本原理是用伪随机测试法检测电路中的易测故障，同时用确定性测试生成法对电路中的难测故障进行测试，以实现在较短的时间内达到较高的故障覆盖率。主要特点是它可以通过改变伪随机测试图形和确定性测试图形的比率在测试时间和测试数据存储量之间进行平衡。如图3所示。其中L表示伪随机测试序列的长度，S表示确定性测试图形的长度。从图中可看出伪随机测试的长度是一个非常重要的参数。伪随机测试长度短，则需要较大的确定性测试集，这就需要较大的存储空间来存储确定性测试图形，但同时也使得测试时间缩短。相反，伪随机测试长度长，则测试施加时间长，但所需的确定性测试集小，需要的存储空间也小（面积开销就小）。

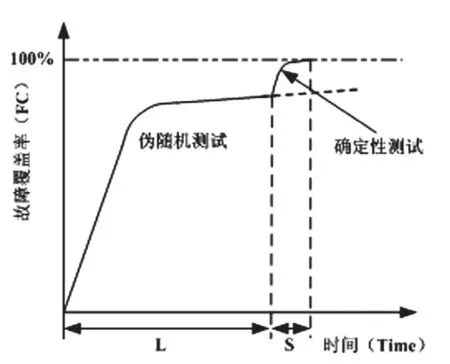
图3 混合测试生成法测试时间与故障覆盖率关系

2.2.1 映射测试图形法

映射测试图形法[4-5]是把LFSR的状态映射成确定性测试图形的一种方法[6-7]。这种方法可以通过增加额外电路以产生控制信号来控制某些LFSR的位翻转或者使其固定0或1来实现。这种方法的开销主要来自产生控制信号的硬件电路，因为对于给定的被测电路和LFSR，这些额外电路需要全定制来实现。一种有效的方法是把LFSR生成的测试图形转换成新的测试图形以得到高的故障覆盖率。这种转换可以通过在TPG和被测电路之间插入映射逻辑来实现。映射逻辑把无效测试集（不能检测到故障的测试集）转换成可以检测难测故障的测试向量。然而，大多数情况下，这种控制LFSR伪随机序列位的方法并不能完全解决难测故障的问题。

2.2.2 重复播种法

重复播种法[8-11]先对电路施加一定数量的伪随机测试图形，用以测试电路中的易测故障，而对于确定性测试图形则将其编码为“种子”，将其重复播种到测试生成器中，用以测试难测故障。由于这种方法重复用新的种子初始化伪随机测试图形生成器，因此这种方法不仅能达到非常高的测试覆盖率，而且可以在测试时间和测试开销上进行均衡，并使测试具有较大的灵活性和可预见性。现已成为BIST中研究最多的测试生成方法。

常用的重复播种法主要包括：（1）多多项式LFSR重复播种方法。此方法利用了多多项式线形反馈移位寄存器（MP-LFSR）来实现，所谓的MP-LFSR是指同一电路结构可以实现一个给定长度LFSR的不同本原多项式，这样保证了一个测试向量可以被成功的编码成功。通过理论和实践证明，采用多多项式LFSR重复播种方法，种子的位数只需要达到Smax＋4（参数Smax是测试集中所有测试向量所含确定位的最大数目），就可以把测试向量不能被编码成功的概率降低到10~6以下。这比单个多项式LFSR重复播种方法所需要的Smax＋20的种子长度明显优越得多，从而提高种子的编码效率和数据压缩率。但这种方法的设计比较复杂，增加了硬件开销。（2）变长种子LFSR重复播种方法。此方法也是基于MP-LFSR的重复播种方发，不同的是这种方法在对种子进行编码的时候，选用的种子要尽可能短，使得种子的长度存在差异，不同的测试向量经过编码可能得到不同长度的种子，这种方法进一步提高了编码的效率和测试压缩率。但这种方法需要对种子进行长度筛选，电路设计难度增大，测试过程较复杂。（3）部分动态LFSR重复播种方法。所谓的动态重复播种是指在测试过程中不断的变换种子，保证测试向量的编码自由度被保留下来，用于求解接下来的测试向量，这样编码效率得到了提高。部分动态LFSR重复播种的方法最大特点是动态重复播种与扫描链装载是同时进行的，减少了测试生成时间，降低了测试开销。但求解种子的方程组规模较大，增加了求解种子的复杂度。

3 发展方向

以上的新兴测试方法虽然相比较传统的测试生成方法在一定程度上提高了测试效率，但如果直接存储用于测试难测故障的测试向量需要较大的存储空间，因而会增加硬件的开销，从而增加了测试开销。因此在使用新兴的测试方法，特别是重复播种方法时如果能对测试数据进行压缩，则可以减小测试数据的存储空间，达到降低测试开销的目的。

近年来人们对测试数据压缩主要分：（1）纵向压缩，即主要压缩种子的数目；（2）横向压缩，即压缩测试向量的位数。但这两种方法都没有最大限度的利用种子，种子的利用率是可以进一步挖掘的，也就是说同一个种子实际上可以检测出更多的故障，提高种子的利用率必然也会降低种子的数目，降低测试开销。因此如果能够同时对种子进行横向和纵向的压缩，则会实现对测试数据最大限度的压缩，提高种子的利用率。

另外，对于现在的SoC电路大多采用IP复用的方法来设计，这些内嵌式的IP都有着自己固定的测试方法，如果利用内建自测试测试生成方法对这些电路进行测试，并使得测试成本降到最低也是一个重要的研究方向。

[1] H. Fujiwara, Lo gic Testing and Design for Testability[M], MIT Press, Cambridge, MA, 1986.

[2] 雷绍充, 邵志标, 梁峰, VLSI 测试方法学和可测试性设计[M], 北京：电子工业出版社, 2005.

[3] Nur A. Touba and Edward J. McCluskey, Test Point Insertion Based on Path Tracing[C], IEEE Proceedings of 14th VLSI Test Symposium, pp. 2-8, 1996.

[4] Touba, N.A. and E.J. McCluskey, Transformed Pseudo-Random Patterns for BIST[C], Proceedings of VLSI Test Symposium, pp. 410-416, 1995.

[5] Touba, N.A. and E.J. McCluskey, Synthesis of Mapping Logic for Generating Transformed Pseudo-Random Patterns for BIST[C], Proceeding of International Test Conference, pp. 674-682.

[6] N. A. Touba and E. J. McCluskey, Synthesis of Mapping Logic for Generating Transformed Pseudo-Random Patterns for BIST[C], IEEE VLSI Test Symposium,pp.674-682, 1995.

[7] H.-J. Wunderlich and G. Kanchan, Bit-Flipping BIST[C], IEEE International Conference on CAD-96,pp. 337-343, 1996.

[8] Bernd Konemann, LFSR-Coded Test Patterns for Scan Designs[C], Proceedings of European Test Conference,pp. 237-242, 1991.

[9] S. J. Venkataramann, Rajski, S. Hellebrand and S.Tarnick, An Efficient BIST Scheme Based on Reseeding of Multiple Polynomial Linear Feedback Shift Registers[C], Proceedings of International Conference on Computer-Aided Design (ICCAD), pp. 572-577,1993.

[10] A. A. Al-Yamani, E. J. McCluskey, Built-In Reseeding for Serial BIST[C], Proceedings of VLSI Test Symposium, Apr. 2003.

[11] D. Kagaris, Multiple Seed TPG Structures[J], IEEE Transactions on Computers, Vol. 52, No. 12, pp. 1633-1639, Dec. 2003.