天气雷达回波数据的压缩实验

史昶彬

（南京邮电大学 南京 210003）

0 引言

网络雷达能够提供更广的覆盖范围、实现空域的精细化测量，进一步提高对灾害性天气的监测预警能力。在网络雷达中，雷达作为一种没有人机交互界面的传感器，采集到的数据经过必要的处理，再通过通信电路（如E1）传输到控制中心。目前，国外的网络雷达是通过100~300Mb的高速数据网进行数据传输，这种传输成本在国内是不能接受的，必须通过必要的技术手段降低数据传输率，有效地使用国内的通讯传输网。

目前对于天气雷达数据压缩，有人产生了结合小波变换和熵编码的灵感，考虑到基于游程和可逆整数小波变换技术的天气雷达数据压缩技术，包括使用可逆整数小波变换和位平面编码的无损压缩技术或者使用整数映射为整数的小波变换进行有损压缩[1]；通过研究传统的熵编码方法，提出一种基于改进游程编码的综合无失真压缩算法，应用于天气雷达原始数据压缩[2]；将气象雷达原始回波二进制类型数据文件进行无损压缩，将位图压缩算法、哈夫曼压缩算法进行组合，设计位图压缩+哈夫曼压缩算法，此类算法复杂度较大，不适于工程应用[3]。

本文通过一些压缩实验，将雷达回波进行小波变换后的系数进行不同比特数的量化，对量化后的系数采用LZW、算术编码等无损压缩技术，并提出了新的BWT+PPMD的无损压缩方案，分别计算各自的压缩比和信噪比损失，通过发现BWT+PPMD能在相同信噪比损失的情况下获得最好的压缩性能；同时分析了不同压缩比情况下，一维或二维小波变换对信噪比损失的影响，为进一步研究网络雷达数据的传输提供重要的依据。

1 天气雷达数据压缩方案

设计天气雷达数据压缩过程如下 ： 接收端接收信号后，经过解压缩、反量化、小波逆变换来重构原始数据。

1.1 信号重组

气象雷达所探测的物体如云、雨、冰雹等是延续分布在广大空间中的散射介质，为了取得对目标物的分辨力，雷达发射的是一连串窄脉冲信号，而在发射脉冲的间歇期间，依次接收到自近及远的目标物回波信号[4]。本文所采用的是从现场采集的单载频天气雷达雨天原始回波的I和Q数据（见图2），有1114个距离门，64个脉冲，每个数据由24比特表示，因此原始数据大小为1114×2×64×24÷3 =427776Bytes。

为了能充分利用相同距离门64个累积数据的相关性，将其视为一个特殊的二维图像进行处理。在小波变换之前，将一个射线方向上的雷达数据排列成为64×2228（64行，2228列）的数据矩阵，如图1。

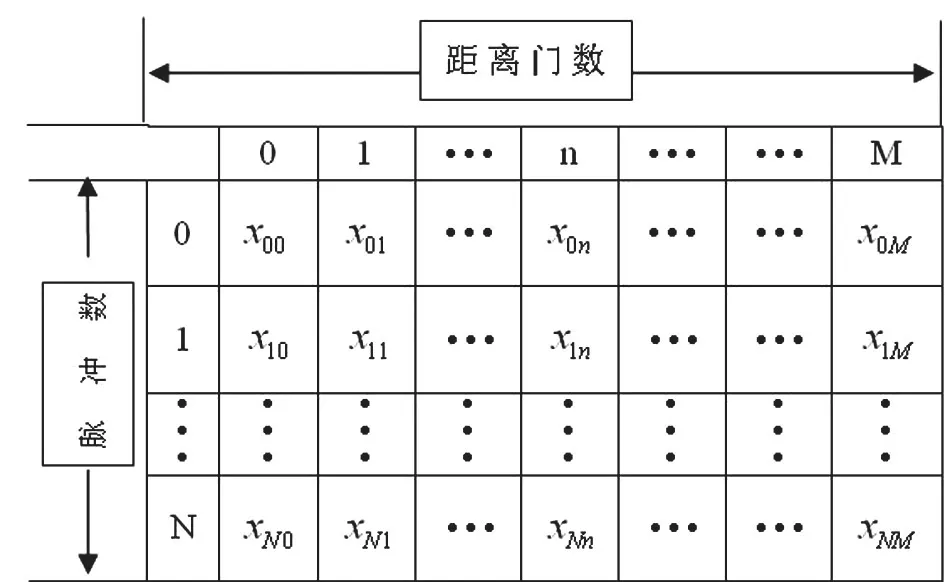
图1 天气雷达雷达数据矩阵

图2 雨天IQ数据

1.2 小波变换

小波变换本质上是一种变换编码，是针对统计冗余进行压缩的方法，具有良好的时域和频域局部分析特性，通过对小波分解域的系数分配不同的量化比特数来实现信号压缩。

研究表明，对于一维信号，一般采用规范正交基，针对不同信号，迅速搜索出想要的正交基，但是雷达信号千变万化，实际中不好实现，比较而言，固定一个平均效果较好的小波基组更为可行；对于二维信号，常用的Daubenchies小波函数系数并不具有最优信号压缩性能，由于具有正交、紧支、对称性的小波变换函数在理论上是不存在的，因此实际常用能量紧支性接近正交变换的双正交小波变换。本文选取bior1.1小波，通过小波变换，去除输入数据的一部分相关性，实现变换域中信号能量的集中，量化时赋予不同的比特数便实现了压缩。

本文分一维和二维小波分解2种情况分别讨论，以便分析出不同的小波变换对信噪比损失和压缩比的影响。

1.3 量化

小波变换后，数据的定义域由整数变成了范围大得多的浮点数，存储这些浮点数其实比存原始信号占用了更多的空间，因此有必要对这些浮点数实施量化步骤。量化的方法有很多种，一般来说，效果越好，实现起来也越复杂。矢量量化是一种失真较小的量化技术，但也有不利的一面，比如算法复杂，而且经过小波变换去相关后，邻近小波系数的相关性较小，矢量量化优势并不明显。在此，本文采用通用性较强，且易于实现的均匀量化的方案，量化可以选择不同的量化比特数（6bit-16bit）。

1.4 无损压缩编码

现有的无损压缩主要有2种形式：统计模型，比如Huffman Coding，Arithmetic Coding；字典算法，比如LZW算法[5]。无损压缩的迅速发展催生了 如 ：BWT（Burrows Wheeler Transformation） 编码算法、动态马尔科夫压缩编码（DMC）、PPM（Prediction by Partial Matching）编码。BWT[6]是由Michael Burrows 和 David Wheeler于 1994年提出的一种用于无损压缩的数据变换方法，它本身并不是一种压缩算法，而是基于数据块的字母矩阵进行轮换，对块即字符串轮转换后产生的矩阵进行排序，然后再抽取矩阵的某列作为变换的结果代替原串，从而调整了压缩元素之间的相对顺序来提高压缩比和压缩速度。PPM数据压缩算法是由Cleary和 Witten 于1984年提出的一种上下文统计模型技术[7]。它根据输入字符中一定长度的上下文后面字符出现的次数，得出每个上下文的预测概率，随后根据该概率用算术编码进行编码，而且PPM是一种自适应技术，每个上下文模型的预测概率将会随着输入字符串的改变而改变。随后各国专家提出PPM的优化衍生算法，如PPMC、PPM*、PPMII、PPMD。

本文结合BWT的压缩速度与PPM的高压缩比，提出一种先BWT变换，再PPM压缩的无损压缩算法。

2 仿真分析

为了验证本文提出的算法，用MATLAB进行仿真，对实地采集的雨天雷达原始数据进行压缩试验。算法采用bior1.1进行5层小波分解。

各种压缩算法的优劣要通过压缩性能评价指标来综合分析。作为一个性能优越的压缩算法，不仅要求具有较高的恢复精度，还要求有理想的压缩效率，但是它们是相互 矛盾的，实际应用中只能折中选取方案。目前常用的压缩评价指标包括相似性指标[8]：CC（Cross Correlation）、PRD(Precent Root mean square Difference)、RMSE（Root Means Square Error）；误差指标：PE（Peak Error）等。本文采用信噪比损失作为评价算法性能的指标。由图2，距雷达近的数据采样值较大，距雷达远的数据采样值较小，为了探寻算法对不同距离的采样点信噪比损失的影响，选取第58和1957个距离门信噪比损失作为样本（分别以SL1、SL2表示）来比较。

对于单载频天气雷达，距离中心雷达越近，各距离门样点的信噪比越大；距离中心雷达越远，各距离门样点的信噪比越小。由图3、图4可以看出，随着量化比特数的减少，各采样点信噪比均有所下降（量化误差引入了量化噪声）；远距离门采样点的信噪比恶化速度要比近距离门采样点的信噪比的恶化速度快。

图3 SL1、10比特、6比特、量化后的频谱

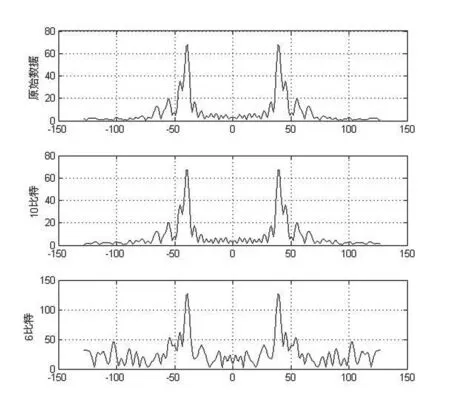
图4 SL2、10比特、6比特、量化后的频谱

系统的实验结果如表1所示。

从表1可以看出，随着量化比特数的减小，压缩比也越小，甚至可以达到12倍，但是CC、PRD、RMSE等压缩指标在压缩比满足条件的同时都有所恶化；各距离门的信噪比损失也会随着量化比特数的减小而增大。

PPMD的压缩性能要高于LZW和算术编码，而通过BWT的字符轮换变化后，再进行PPMD压缩，压缩比又得到了一定的提高。

由图5可以看出，在量化比特数相同的情况下，若压缩倍数小于等于7，则经二维小波变换后的信噪比损失要小于一维小波变换后的信噪比损失；若压缩倍数大于等于7，则经二维小波变换后的信噪比损失要大于一维小波变换后的信噪比损失。压缩比与信噪比损失始终是一对相互矛盾的性能指标，在比对各项性能数据之后，发现了一个性能转折点，即在压缩倍数小于7时，二维小波变换性能要优于一维小波变换，这为用户选择量化比特数与方法时，提供了一个可参考的临界值，若要求压缩倍数大于10倍，建议采用一维小波结合BWT+PPMD的压缩方案。

3 结束语

本文通过结合BWT的压缩速度和PPMD的压缩效率，提出了一种小波变换、均匀量化、和BWT+PPMD的天气雷达数据压缩算法，实验结果表明该算法较LZW和算术编码的压缩比高，实验具有显著实用价值。然而，当前对于天气雷达原始IQ数据的压缩仍然是一个崭新的课题，有待根据数据特性进一步提出优化方案。

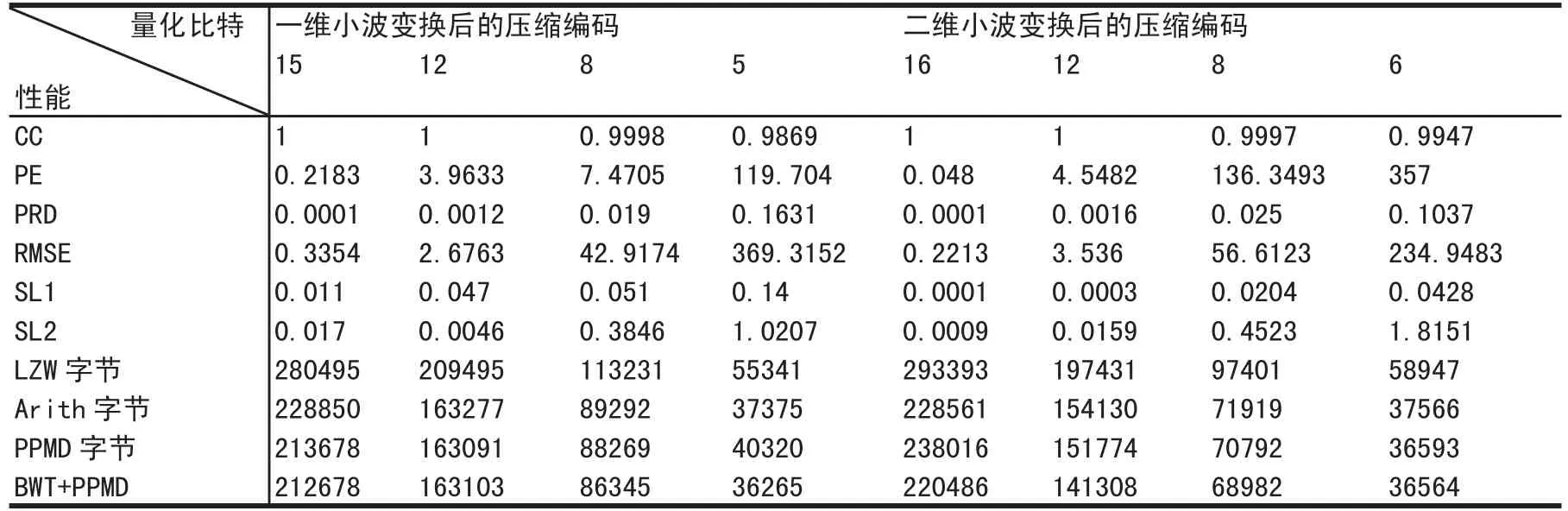
表1 量化性能对照表

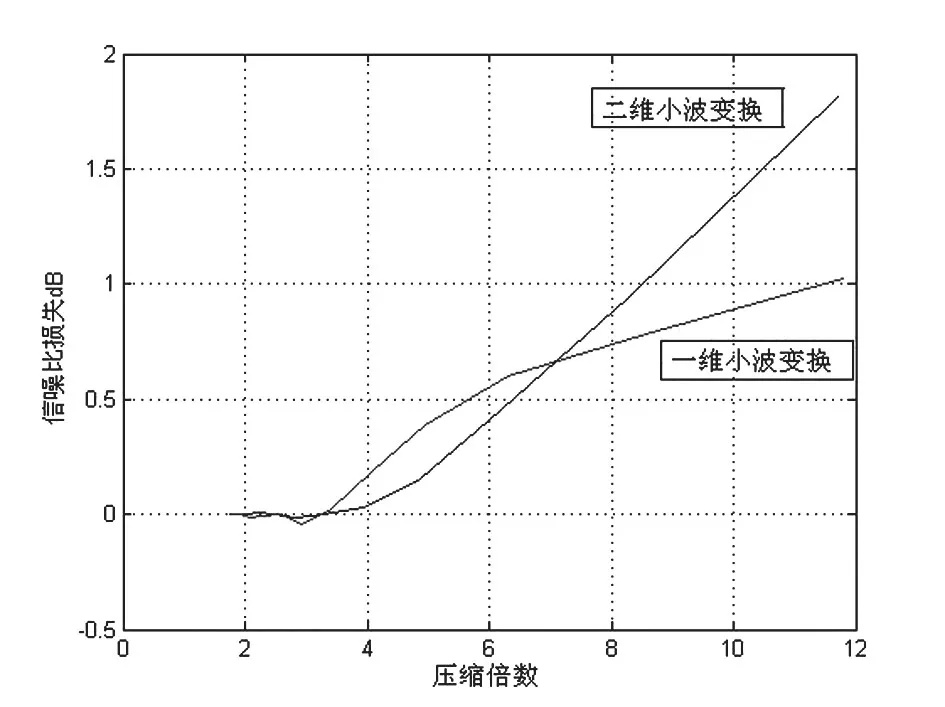
图5 压缩比与信噪比损失曲线

[1] Yan Wei，Zhu Zhaoda，Wang Qingdong，Ma Ning，Some new techniques used in digital weather radar networking and composition，CIE International Conference of Radar Proceedings，2001：874-877.

[2] 黄锐, 唐继勇. 文本类型气象雷达原始回波数据的无损压缩[J]. 通信与信息技术, 2008(01).

[3] 马宁, 朱福萌, 尹志军, 蒋林辉. 改进游程编码在天气雷达数据压缩中的应用[J]. 解放军理工大学学报：自然科学版， 2004(06).

[4] 焦忠生，沈超玲.气象雷达原理[M].北京：气象出版社，2005.

[5] 吴乐南.数据压缩的原理与应用.北京：电子工业出版社,1995.

[6] Burrows M , Wheeler D J . A Block - sorting Lossless Data Compression Algorithm [ R ] . SRC Research Report 124 [ s. l . ] :Digital Systems Research Center,1998.

[7] J.Cleary and I. Witten, Data compression using adaptive coding and partial string matching, in IEEE Transactions on Communications, 1984，COM-32(4).

[8] 高永丽. 信号处理中的数据压缩评价指标研究[J]. 楚雄师范学院学报, 2008(03).