一种改进的多载波系统均衡算法

王 超 赵东峰 周贤伟 杜利平

(北京科技大学信息工程学院,北京100083)

一种改进的多载波系统均衡算法

王 超 赵东峰 周贤伟 杜利平

(北京科技大学信息工程学院,北京100083)

提出了一种利用改进球译码算法实现滤波器组多载波系统(FBMC)的均衡算法。对基于球译码算法的FBMC均衡算法性能进行了分析,说明了算法的最优性。并进一步推导了改进球译码算法降低经典球译码算法复杂度的基本原理。计算机仿真结果表明:改进球译码均衡算法明显优于迫零算法,在显著降低算法复杂度的同时,性能损失较小。

滤波器组多载波;OFDM/OQAM;球译码;均衡

1.引 言

滤波器组多载波(FBMC)通信技术[1],由于其相对于CP-OFDM技术[2]具有更高的频谱效率,定时、频偏估计灵敏度低,且作为多载波通信技术,具有较高的射频效率[3],被称为未来的多载波通信技术。

在时变多径信道条件下,接收机输入端一般包含符号间干扰和载波间干扰,而不理想的同步与信道估计会进一步加重干扰的影响,从而需要进行接收端均衡[4-5]。当前,FBMC的均衡技术是其研究热点之一[6-7]。

本文提出了一种利用改进球译码算法实现FBMC系统均衡的算法,并对原算法进行了改进,降低了算法复杂度。理论分析与仿真均证明了算法的优越性。

2.FBMC技术

FBMC的发送基带信号可用式(1)表示

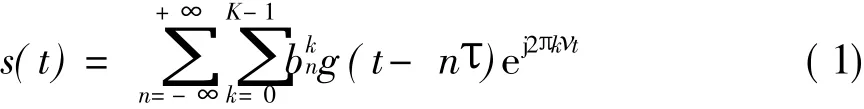
在信道为时变线性信道的条件下,时变单位冲激响为h(t,t′),则接收机解调器输入端接收信号可表示为

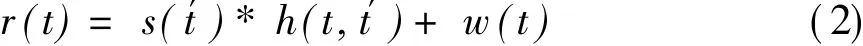
式中:*表示卷积运算;w(t)为均值为0、单边功率谱密度为N0的加性高斯白噪声。

在接收端满足理想定时同步与载波同步条件下,第n个时刻在第k个子载波上基带数字调制符号的解调判决为

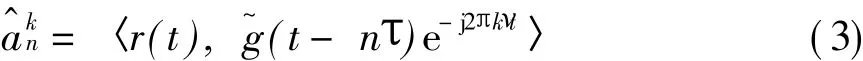
通常的无线信道均存在多径时延扩展与多普勒频展,从而造成频率域与时间域的选择性衰落。而由Gabor小波理论中的Balian定理[8],若需要在接收端抑制衰落,需满足

传统的OFDM系统通过引入循环前缀的方法抑制衰落。但循环前缀的引入造成频谱效率的下降。而FBMC技术的优势即在于,通过选择的波形与函数内积的形式,以及τ、v的取值,在不损失频谱效率的条件下,抑制衰落,实现可靠有效的多载波通信。

3.基于球译码的均衡算法

将发送成形滤波器单位冲击响应g(t)与信道单位冲击响应h(t)级联后组成的系统,按2τ/K的采样率进行采样,得到矩阵记为H0;并记所有bkn组成向量b,

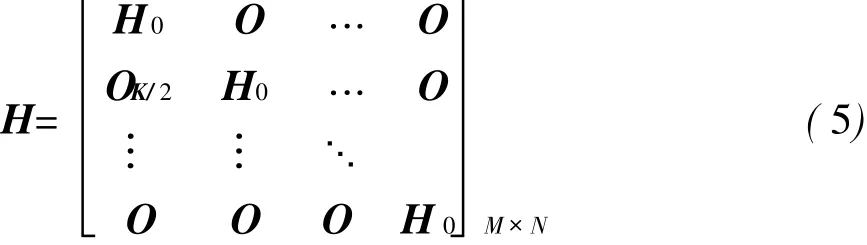
式中:OK/2表示维数为K/2的0向量。则接收信号可表示为

式中:w=(w1,w2,…,wN)′为各加性高斯白噪声组成的向量。

根据ML准则,求解式(6)即是求解具有以下形式的整数最小均方距离问题

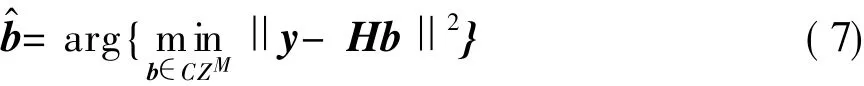
式中:CZM是CZ的M维扩域,而CZ表示各发送天线上所有可能发送复数据组成的集合。

若直接在CZM中寻找满足式(7)的b值,则算法的运算复杂度与CZ中元素个数的M次幂成正比,因而复杂度极高,一般认为是难于实现的。而球译码则在如下一个区间中寻找满足式(7)的b值为

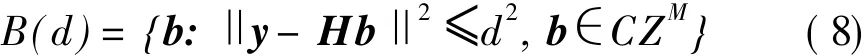
即球译码算法是求解如下的整数最小均方距离问题

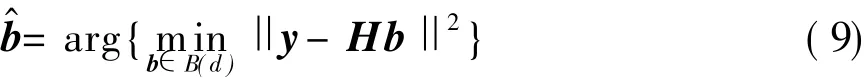
可见,式(8)给出的集合是CZM的子集,因而合理设计的球译码的复杂度可低于直接求解式(7)的复杂度,且若存在满足式(9)的解b^,则b^也是式(7)的解;若式(9)无解,则可以增加d值,当d→∞时,式(9)即与式(7)等价,因而式(9)必然有解,该解即为式(6)的最大似然解。可见,如何确定尽可能小的d值,从而最大限度地减小满足条件的向量数量,是影响球译码算法复杂度的一个关键问题。

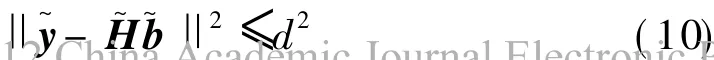
经典球译码算法可以通过按分量展开、逐次迭代的方式实现[10-11]。设矩阵H的QR分解为

式中:R=(rij)是上三角复矩阵;Q=[Q1Q2]是酉矩阵,矩阵Q1和Q2分别由矩阵Q的前M列和后NM列组成。

进一步,式(9)等价于

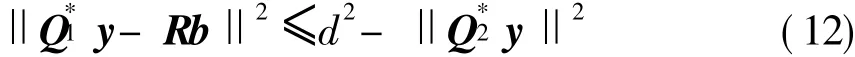
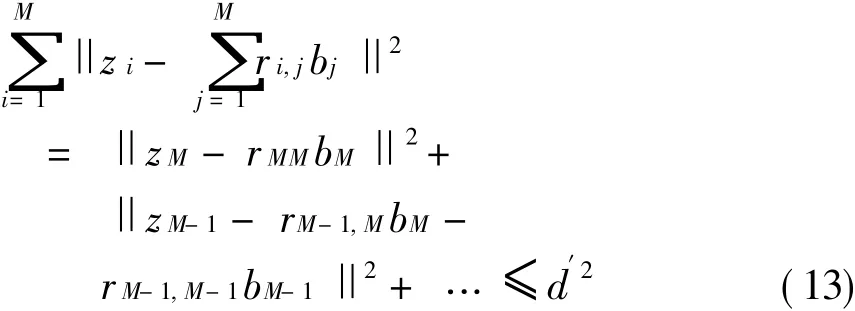
由此,若定义

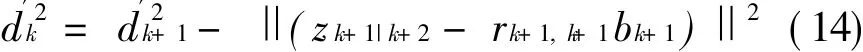
式中:k=1,2,…,M-1,则向量b满足式(13)的条件可表示为

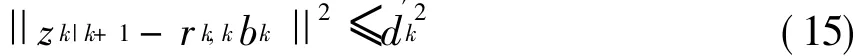
球译码的初始参数可以设置为[10]

式中:σ2是加性白高斯噪声的方差;α则满足

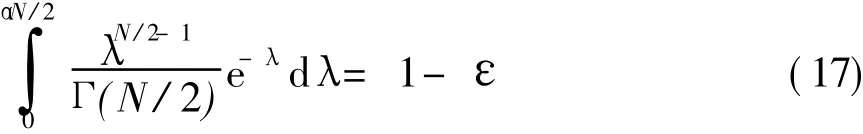
式(17)左边积分式对应的是自由度为N的χ2分布的分布函数在处的取值。而ε则表示当前d值下,式(9)无解的概率[10]。因此,若在式(17)假设下,式(9)无解,则可减小ε值,如取ε=ε2,并重复上述译码过程,直到式(9)有解为止。

而复数域球译码算法的复杂度可以表示为[11]

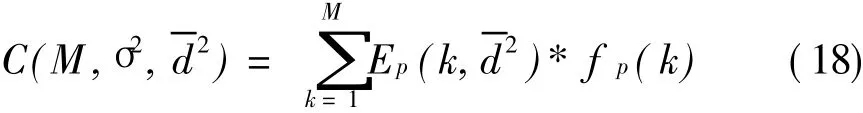
4.算法改进

根据[10-12]经典球译码算法的第k步迭代,式(13)的计算等价为计算下式

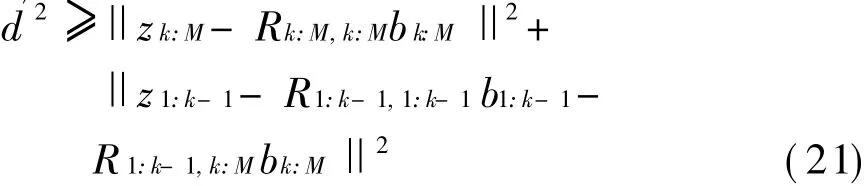
而满足式(21)的必要条件为

因此,若对于任意的b,能够求解式(22)第二加数的一个下界LB(k-1),即存在

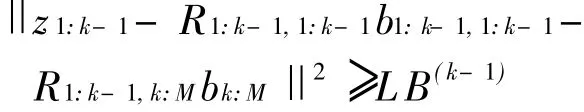
则求解式(22)即可变为求解下式

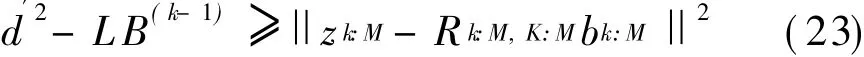
显然,满足式(22)的向量b数量不超过满足式(23)的向量b的数量,因此,计算式(23)可减小式(12)中的取值,从而降低球译码算法的复杂度。LB(k-1)越大,改进球译码的复杂度也越小。

综上,求解式(22)有助于减小球译码的复杂度。但式(22)本身也是一个整数最小均方问题,故精确求解式(22)所带来的复杂度增加值一般不会小于利用式(12)解得到的复杂度减小值。因此,本文提出一种概率估算式(22)的方法,该方法不增加计算式(22)带来的运算复杂度,却能够减小球译码算法本身的复杂度。

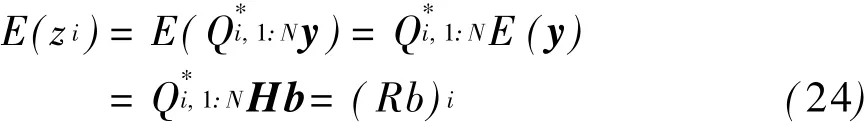
式中:(Rb)i表示向量Rb的i分量;

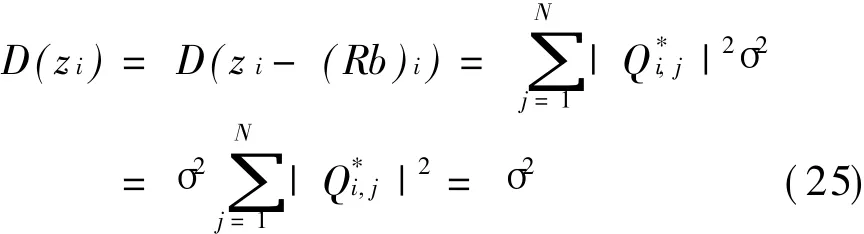
结合式(6)、式(25)可见,若当前展开分支路径为正确路径时,有

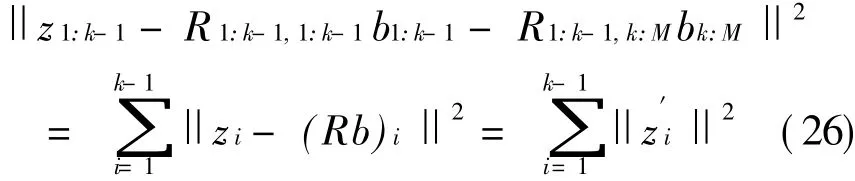
即式(22)不等式左端是(k-1)个独立同分布的复高斯随机变量的平方和,其中,任一高斯随机变量均值均为0,方差为σ2.若当前展开分支内不包含正确路径,此时,设正确路径为b′,则有

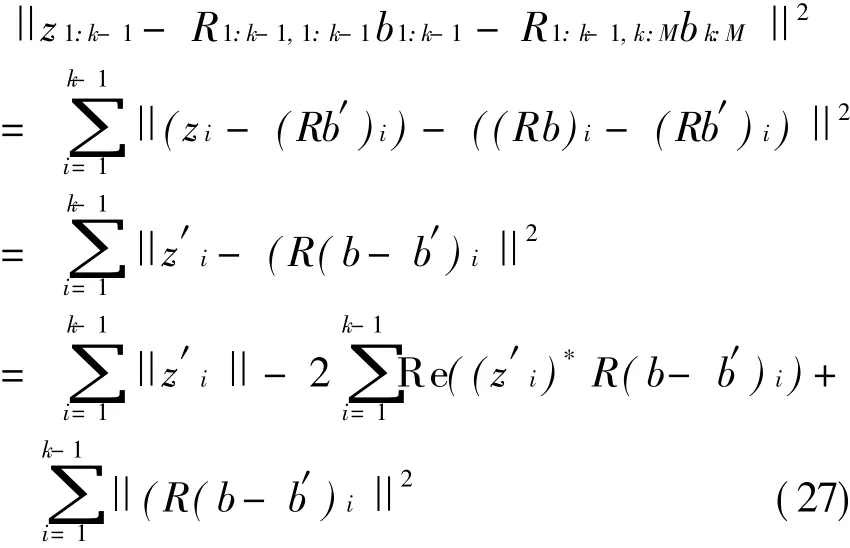
可见,在数据符号与统计量z′i是独立条件下,式(27)的期望满足

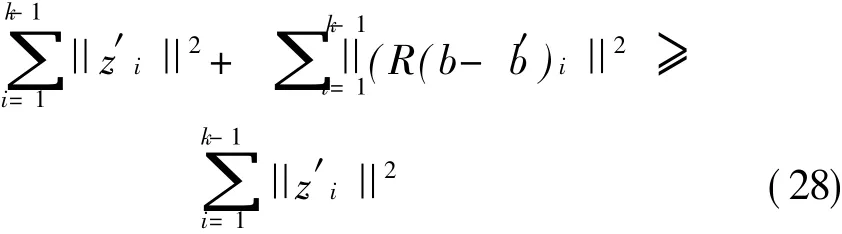
因此,无论当前展开分支路径是正确路径还是错误路径,式(22)均以高概率超过

根据式(17),经典球译码的初始半径是通过概率计算确定的。因而可进一步考虑根据概率计算表达式的可能取值。

总结上述各步骤,修正球译码算法可描述如下

第1步:

第2步:

第3步:

选择bk的一个不同于以往选择的可能取值。

第4步:

k=k+1;如果k=M+1,算法结束;否则,执行第3步。

第5步:

第6步:

表示找到式(6)的解,故存储b,进而执行第3步。

5.仿真结果

上述理论分析的性能均与滤波器组的频响有关,因此,下文采用仿真的方法,验证算法的具体性能。

仿真中采用QPSK调制,取g(t)为滚降系数为0.25的根升余弦滤波器,载波总数N=64,门限η= N2/4,载波块长M=32.信道为等功率分布的3径瑞利随机时变信道,多普勒频移为载波块长的1%。

图1仿真分析了算法的误码率,并与迫零算法的性能进行了比较。图2比较了改进球译码算法与经典球译码算法的译码复杂度。

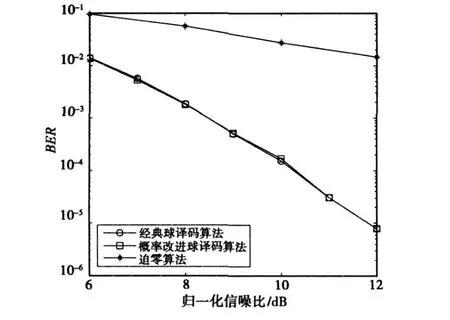
图1 算法的误码率性能对比

由图1、图2可见,算法的误码率性能远优于迫零算法,而改进球译码算法的复杂度远低于经典球译码算法的复杂度,且性能损失不大。

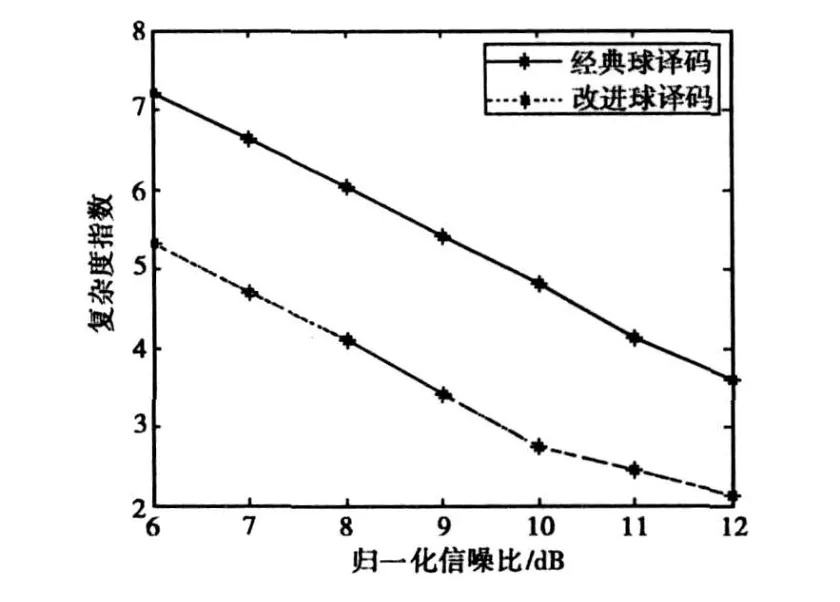
图2 算法的复杂度对比

6.结 论

本文针对FBMC多载波通信技术中的均衡算法进行了研究。提出了利用改进球译码算法实现FBMC系统均衡的均衡算法。对基于球译码算法的FBMC均衡算法性能进行了分析,说明算法为最大似然序列均衡算法,并进一步推导了改进球译码算法降低经典球译码算法复杂度的基本原理。计算机仿真结果表明:改进球译码均衡算法误码率方面明显优于迫零算法,并且在显著降低算法复杂的同时,性能损失较小。

[1] SIOHAN P,SICLET C,LACAILLE N.Analysis and design of OFDM/OQAM systems based on filterbank theory[J].IEEE Trans on Signal Processing,2002, 50(5):1170-1183.

[2] BINGHAM J A C.Multicarrier modulation for data transmission:an idea whose time has comes[J].IEEE Communication Magazine,1990,28(5):5-14.

[3] JUNG P,WUNDER G.The WSSUS pulse design problem in multicarrier transmission[J].IEEE T rans on Communication,2007,55(10):1918-1928.

[4] HIROSAKI B.An analysis of automatic equalizers for orthogonally multiplexed QAM systems[J].IEEE T rans on Commun,1980,28(1):73-83.

[5] IHALAINEN T,STITZ T H,RENFORS M.Eff-i cient per-carrier channel equalizer for filter bank based multicarriersystems[J]. Global Communication, 2008,49(6):3175-3178.

[6] 邵怀宗,吴 颖.一种新的适用于高阶QAM 系统的均衡算法[J].电波科学学报,2009,24(5):961-964. SHAO Huaizong,WU Ying.A novel equalization a-l gorithm for high-order QAM system [J].Chinese Journal of Radio Science,2009,24(5):961-964.(in Chinese)

[7] 曹士坷.一种新颖的单天线抗干扰频偏半盲均衡器[J].电波科学学报,2008,23(3):510-513. CAO Shike.Novel single-antenna interference-rejection FRESH sem-i blind equalizer[J].Chinese Journal of Radio Science,2008,23(3):510-513.(in Chinese)

[8] MALLAT S.A Wavelet Tour of Signal Processing [M].2nd ed.Academic Press,1999.

[9] CIBLAT P,SERPEDIN E.A fine blind frequency offset estimator for OFDM/OQAM[J].IEEE T rans on Signal Processing,2004,52(1):291-296.

[10] HASSIBI B,VIKALO H.On the sphere-decoding algorithm I.expected complexity[J].IEEE T rans. Signal Process,2005,53(8):2806-2818.

[11] VIKALO H,HASSIBI B.On the sphere-decoding algorithm II.generalizations,second-order statistics, and applications to communications[J].IEEE Trans on Signal Process,2005,53(8):2819-2834.

[12] 赵东峰,金 鑫,李道本.多天线系统的一种改进软判决译码算法[J].电波科学学报,2008,23(5): 905-910. ZHAO Dongfeng,JIN Xin,LI Daoben.M odified soft-decision decodingalgorithm formult-i antenna system[J].Chinese Journal of Radio Science,2008, 23(5):905-910.(in Chinese)

An improved equalization algorithm for mult-i carrier system

WANG Chao ZHAODong-feng ZHOU Xian-wei DU L-i ping
(School of Inf ormation Engineering,University of Science and Technology Beij ing,Beijing 100083,China)

An equalization algorithm based on modified Sphere-decoder for FBMC is proposed in this paper.T he excellence of the algorithm is analyzed.T he principle of the reduction of the modified algorithm is further deduced.Computer simulations verify that the algorithm outperforms the zero-forcing algorithm,and the performance loss of the modified algorithm is comparatively small.

FBMC;OFDM/OQAM;Sphere-decoder;equalization

周贤伟 (1963-),男,四川人。北京科技大学信息工程学院教授,博士后,主要研究方向为无线通信、电波传播技术、网络安全和下一代网络。

TN911.22

A

1005-0388(2010)03-0564-05

王 超 (1978-),男,河北人。北京科技大学信息工程学院讲师,研究方向为无线通信、信号检测、高速实时信号处理。

赵东峰 (1976- ),男,山东人,现为北京科技大学信息工程学院讲师,研究方向为未来移动通信中物理层技术。

2009-08-28

国家自然科学基金(60773074);(60902042)资助项目

联系人:王超E-mail:wanch3307@sohu.com