径向线馈电网络的模式转换与单模传输条件分析

李相强 刘庆想 赵 柳 张健穹

(西南交通大学物理科学与技术学院,四川成都610031)

径向线馈电网络的模式转换与单模传输条件分析

李相强 刘庆想 赵 柳 张健穹

(西南交通大学物理科学与技术学院,四川成都610031)

在高功率径向线阵列天线的设计中,径向线内高阶模的产生过程分析及其抑制方法研究具有重要的意义。通过将模式匹配法应用到径向波导,给出了一种计算径向线馈电网络中模式转换的方法,以微波向内传输和微波向外传输的两种具体情况为算例,对因耦合探针的插入引起的微波模式转化进行了定量的类比计算,得到了产生的微波模式阶数与探针个数的定量关系,并以此为基础分析给出了馈电网络中单模传输的必要条件。结果表明:为了保证径向线馈电网络的单模传输,在径向线的一定位置处可以插入的探针个数受上限和下限的双重制约,且在实际设计中应尽量选择限定条件的中间部分来确定阵列天线的布局。

模式匹配法;高阶模;阵列布局;耦合探针;径向线

1.引 言

为了实现高功率微波的定向辐射,国内学者新近提出了一种新型的高功率径向线阵列天线[1-5],这类天线采用径向线为馈电网络,通过耦合探针从径向线中提取能量激励单元天线。在该类天线的设计过程中,一项非常重要的工作是避免馈电网络中高阶模的产生,实现单模传输。这是因为馈电网络中高阶模的存在会破环能量沿圆周方向分布的均匀性,给探针的能量耦合带来很大难度;另外,产生的高阶模跟频率有较大的关系,随着频率的变化,高阶模的模式和分布都会产生一定的变化,使得探针的耦合幅度发生较大的变化,从而恶化馈电网络的频率特性。因此,径向线阵列天线馈电网络中高阶模的产生过程分析及其抑制具有重要的意义。

当输入模式为角向均匀的径向TEM模时,馈电网络中的高阶模都是由结构的不均匀性引起的,具体到径向线阵列天线的馈电网络,则主要是由于耦合探针的插入产生的。然而由于径向线的特殊性,其传输截面为圆柱面,一般的数值模拟软件无法对其中的微波模式进行模拟,所以难以对馈电网络中高阶模的产生及传输过程进行系统准确的分析。相关研究表明,模式匹配法是在分析波导截面规则突变时常用的一种方法,它可以对突变截面前后的微波模式进行准确的计算[6-8],为此我们将其应用到径向线阵列天线的馈电网络中,分析其中的微波模式转化并讨论其中的单模传输条件。

2.问题的描述

在多数情况下,径向线阵列天线馈电网络的结构非常复杂,要全面分析其中的微波模式具有一定的难度。由于我们关心的仅是高阶模的产生与传输,不涉及能量耦合过程,因此可将同一圆周上均匀分布的探针类比为均匀分布的导体板,如图1所示。在图中所示的结构下,以微波沿径向向内传输为例,需要经过两处波导截面突变和一次波导内传输的过程,即首先在第一个突变处由径向线转换为柱面喇叭波导(界面A),然后在柱面喇叭波导中传输,最后在第二个突变处由柱面喇叭波导转换为径向线(界面B)。在这一过程中,输入的柱面T EM模在圆周方向的均匀性会受到影响而产生高阶模。

要对这一过程进行分析,重点就是要计算界面A和界面B处的模式转化情况。由于两处的波导转换都是波导截面的规则突变问题,因此可将传统的模式匹配法进行推广,应用到径向波导中,计算转化过程中的透射模式、反射模式及其幅值。

图1 径向线内均匀分布的导体板

3.径向波导内的模式匹配法

模式匹配法的原理是将所研究区域内的场视作多个模式的叠加,用正交级数将变截面两端的电磁场近似展开,根据变截面上电磁场的匹配条件,求解各模式对应的系数,最终得到各模式的透射系数及反射系数[8]。下面阐述将其应用于径向波导内的求解方法和步骤,由于界面A和界面B处的求解完全类似,仅以界面A处的模式计算为例进行说明。

微波在界面A上的波导转换可用图2所示的等效双端口网络来描述,由图中可以看出,将界面A两端的结构划分为两个区域,区域I为径向线,区域II由多个夹角为α的柱面喇叭波导组成。在通常情况下,径向线内的输入模式均为柱面TEM模,它具有完全的圆周对称性,使得区域II的所有柱面喇叭波导具有完全一致的对称性,里面所产生的模式也完全一致,因此区域II虽然由多个柱面喇叭波导组成,但可以看作一个端口,其中的模式可根据单个柱面喇叭波导内的模式定义。

假设区域I、区域II分别存在P、Q个微波模式,则区域I内的横向场可表示为

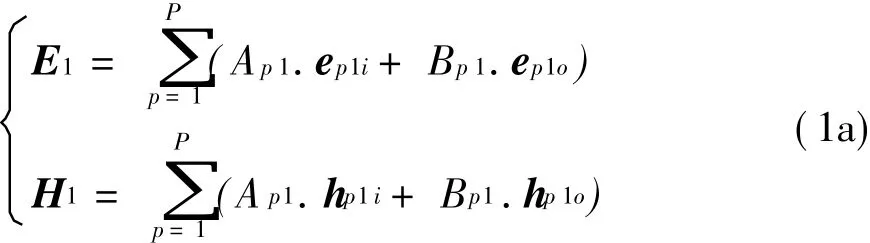
区域II内的横向场可表示为

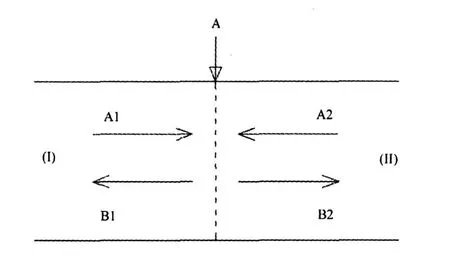
图2 向内传输的波导转换过程

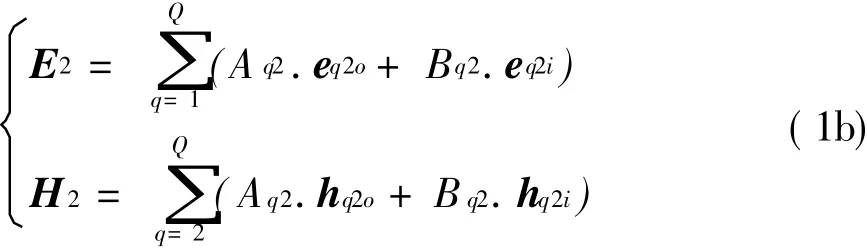
式中:Ap1、Bp1分别为I区中入射场和反射场的第p个模式的系数;Aq2、Bq2分别为II区中入射场和反射场的第q个模式的系数;ep1i、hp 1i表示区域I中向内传输的第p个模式的横向电场和横向磁场的矢量模式函数;ep1o、hp1o表示区域I中向外传输的第p个模式的横向电场和横向磁场的矢量模式函数;eq2i、hq2i表示区域II中向内传输的第q个模式的横向电场和横向磁场的矢量模式函数;eq2o、hq2o表示区域II中向外传输的第q个模式的横向电场和横向磁场的矢量模式函数。

径向波导中微波模式的划分经常借用常规波导的方法进行,即按照Hz=0和Ez=0来划分,分别记作TM(z)和T E(z)[9].但在径向波导中,由于其传输截面为变截面,其中传输的微波模式与常规波导相比有一定的区别,主要体现在:(1)与常规波导中一个模式对应一个场分量表达式不同,在径向波导中,向内传输和向外传输的同一个微波模式对应的场分量表达式并不完全相同,而是有一个系数的差别;(2)与常规波导中仅有传输模和截止模两类模式不同,在径向波导中,模式的传输和截止状态还与其所在的位置有关,存在传输模、截止模和逐渐截止模式三种情况[10],其中传输模在径向波导内任何位置处都处于传输状态,它关于ρ呈汉克尔函数的关系,截止模在径向波导内任何位置都处于截止状态,它关于ρ呈虚宗量贝塞尔函数或虚宗量汉克尔函数的关系,而对于逐渐截止模式,存在一个ρ0值,使得在ρ≥ρ0的区域内,该模式是传输的,而在ρ﹤ρ0的区域内,该模式是截止的,这时它与ρ之间的关系一般用单独的贝塞尔函数或诺依曼函数表示;(3)由于径向线具有圆周对称性,每个模式的场分量关于 φ都存在多种表达形式,即简并模式,由于每一个简并模式都可以看作两个正交模式的线性组合,因此为了简化计算,将径向线中的每个模式都作为两个独立的正交模式进行处理。

在注意到上述特殊性之后,可根据不同的情况给出横向矢量模式函数,代入式(1)中可得到具体的表达形式(因篇幅所限,不一一列出),表达式中各模式的系数通过电磁场的匹配条件求得。在界面A上,横向场的匹配关系为

式中:s表示界面A上柱面喇叭波导的面积;s′表示界面A上金属板截面的面积;SA=s+s′。

将具体的表达形式代入到上述关系式中,经过正交化处理,可化简得出如下矩阵方程

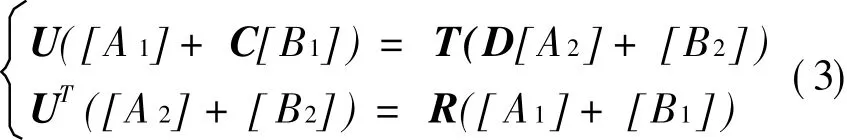
式中:[A1]= [A11…AP1]T;[A2]= [A12…AQ2]T;是前述内行波

和外行波间的系数差别,不再列出。

对矩阵方程(3)进行求解,可以得到界面A上的散射方程

其中散射矩阵的计算式为

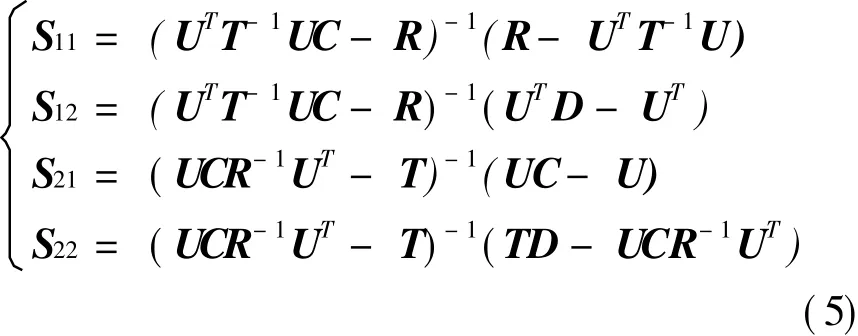
4.算例与结果

4.1 向内传输

微波向内传输的具体算例为:工作频率f=4.0 GHz,径向波导上下板间距h=20 mm,在距离径向线中心135 mm处插入18块厚度为3 mm、长度为 15 mm的导体板,输入微波模式为径向T EM模,计算经过导体板后的微波模式。

首先计算由径向线到柱面喇叭波导的转换过程。在计算时,选取适当的微波模式个数(一般选取所有的传输模和前面的几个逐渐截止模),分别表示出每个模式的横向矢量模式函数,代入到式(5)中通过计算即可得出各模式的系数。计算得到的透射模式及其幅值列于表1中。从表1中可以看出:输入的微波模式在柱面喇叭波导内形成的模式为等角向周期数为奇数的模式。这一结果可以从结构的对称性上来解释:柱面喇叭波导是左右对称的,且激励柱面喇叭波导的径向T EM模在整个角向分布也是完全一致的,因此透射模式一定是左右对称的等模式,而不会是T M(z)02、T M(z)04等模式。

表1 界面A处的透射模式及其幅值

下面分析上述透射模式在柱面喇叭波导内的传输过程。根据各透射模式的电磁场表达式可以计算出传输过程中各模式功率的变化情况,其归一化结果示于图3中(以模式产生处的功率为1)。由图可以看出,上述透射模式在传输过程中,只有模不衰减(未计及导体损耗),而等模式迅速衰减,考虑到在波导转换过程中主要形成的是模,所以可近似认为在下一个转换界面处柱面喇叭波导内仅有模。

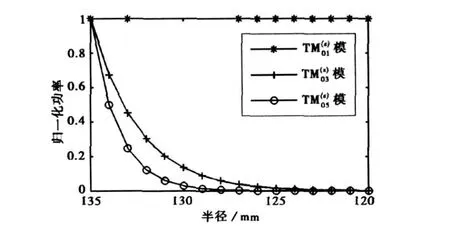
图3 透射模式的归一化传输功率(向内传输)

表2 界面B处的透射模式及其幅值

4.2 向外传输

微波向外传输的具体算例为:工作频率f=4.0 GHz,径向波导上下板间距h=20 mm,在距离径向线中心45 mm处插入6块厚度为3 mm、长度为 15 mm的导体板,输入微波模式为径向TEM模,计算经过导体板后的微波模式,示意图如图4所示。这种情况的计算方法与向内传输时完全类似。

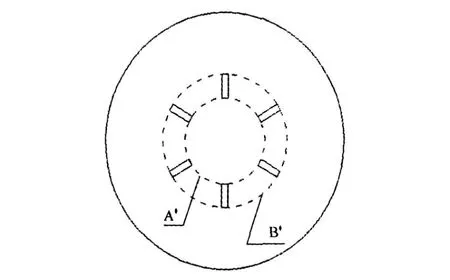
图4 向外传输的转换过程

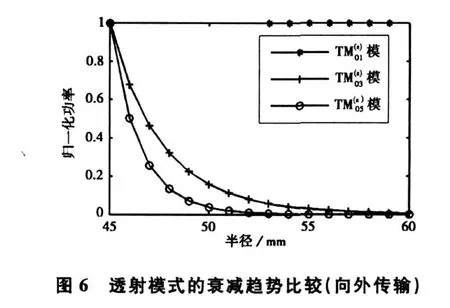
界面A′处的透射模式及其幅值的计算结果列于表3中,透射模式仍为等模式。透射模式的归一化传输功率示于图5中,由图可见,经过一段距离的传输后透射波中近似只有柱面喇叭模。界面B′处的透射模式及其幅值的计算结果列于表4中,从计算结果可以看出,所形成的透射模式的角向周期仍为导体板数量的整数倍,且仅有模为传输模式,但需要指出的是,在60 mm处已具有较强的传输能力(如图6所示),且当ρ＞72 mm时,该模式是传输的,这说明在透射波中除了径向线内的主模模之外,还有一部分的模式,使得径向线沿径向的分布不再完全均匀,会给探针耦合带来一定的困难。

表3 界面A′处的透射模式及其幅值

表4 界面B′处的透射模式及其幅值

5.单模传输条件分析

前面通过两个具体的算例计算了周向均匀分布的导体板对微波传输的影响。已经指出,在馈电网络中一个耦合探针的插入对微波传输的影响与一块导体板的作用类似。这样,利用前面计算得到的相关结论,可以从阵列天线布局的角度对馈电网络中的单模传输条件进行分析。

根据两个算例中得到的结论,径向线中产生的微波模式的角向周期应为该位置处探针个数的整数倍,柱面喇叭波导中产生的模式的角向周期应为奇数。设在某一半径为ρ的圆周上沿角向均匀分布有n个探针(忽略探针占据的角向角度),则为了保证单模传输,即在径向线中只有柱面TEM模(即径向线模)为传输模,在柱面喇叭波导中只有柱面喇叭模为传输模,必然有

即有

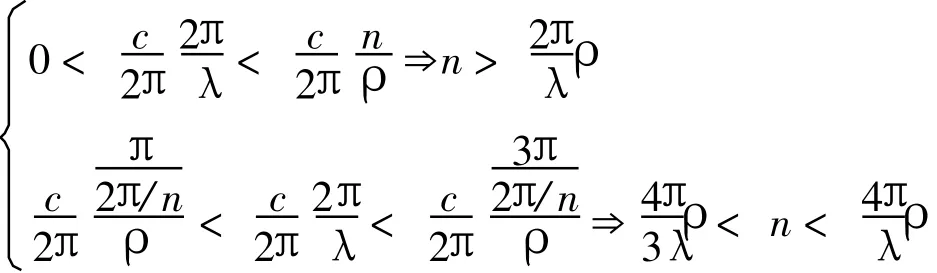
整理可得到

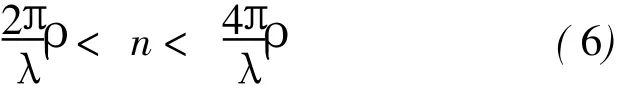
但需要指出的是,式(6)只能作为馈电网络中单模传输的必要条件,实际中n的取值范围要比该式限定的范围小。这是因为在式(6)的推导过程中没有考虑逐渐截止模式,这样当n取到其下限附近时,径向线中产生的第一个高阶模式的衰减较慢,甚至当大于某一个半径值时变成传输状态,这样在有限的传输距离下可能无法完全截止,导致高阶模的传输;而当n取到其上限附近时,柱面喇叭波导中的模虽然理论上为传输模,在实际上处于传输与截止的临界状态,有一定的衰减,导致透射过去的能量不高,容易理解此时的反射模幅值较大,因此,损耗很大。

在实际设计过程中应尽量选取式(6)中限定条件的中间部分,并且还要综合考虑高阶模传输距离、阵列的增益、耦合探针设计的难易等因素来综合确定阵列天线的布局。

6.结 论

通过将模式匹配法应用到径向波导中,对径向线阵列天线馈电网络中高阶模的产生和传输过程进行了分析,认识了微波模式转化的物理过程,得到了一些有用的结论,并以此为基础,从阵列天线布局的角度,分析给出了馈电网络中的单模传输条件,为阵列天线的设计提供了重要的理论基础。

[1] 刘庆想,李相强,袁成卫,等.高功率双层径向线螺旋阵列天线理论分析与数值模拟[J].电子学报,2005, 33(12):2231-2234. LIU Qingxiang,LI Xiangqiang,YUAN Chengwei,et al.Theoretical analysis and numerical simulation of a high power helical array antenna fed from double-layer radial waveguide[J].Acta Electronica Sinica,2005,

[2] 李相强,赵柳,刘庆想,等.高功率径向线螺旋阵列天线理论与实验研究[J].电波科学学报,2008,23(4): 781-785. LI Xiangqiang,ZHAO Liu,LIU Qingxiang,et al. High-power radial line helical array antenna using double-pillar coupled probes[J].Chinese Journal of Radio Science,2008,23(4):781-785.(in Chinese)

[3] LI Xiangqiang,LIU Qingxiang,Wu Xiaojiang,et al. A GW level high-power radial line helical array antenna [J].IEEE trans.on antennas and propagation,2008, 56(9):2943-2948.

[4] 李相强,赵 柳,吴晓降,等.GW级高功率径向线螺旋阵列天线[J].西南交通大学学报,2009,44(2): 215-220. LI Xiangqiang,ZHAO Liu,Wu Xiaojiang,et al.GW-level high-power radial line helical array antenna[J]. Journal of Southwest Jiaotong University,2009,44 (2):215-220.(in Chinese)

[5] 赵 柳,李相强,陈晓波,等.16单元组合式矩形径向线螺旋阵列天线的设计[J].电波科学学报,2008,23 (4):640-644. ZHAO Liu,LI Xiangqiang,CHEN Xiaobo,et al.Design of 16-element assembled rectangular radial line helical array antenna[J].Chinese Journal of Radio Science,2008,23(4):640-644.(in Chinese)

[6] M AT RAS P,BUNGER R,ARNDT F.Mode-Matching Analysis of the step discontinuity in elliptical waveguides[J].IEEE Microwave and guided wave letters,1996,6(3):143-145.

[7] ALESSANDRI F,MONGIARDO M,SORRENTINO R.Rigorous mode matching analysis of mitered E-plane bends in rectangular waveguide[J].IEEE M-i crowave and guided wave letters,1994,4(12):408-410.

[8] 张晓萍,钟辉煌,袁成卫.微波源中同轴提取区支撑杆的理论分析与设计[J].微波学报,2004,20(2): 46-50. ZHANG Xiaoping, ZHONG Huihuang,YUAN Chengwei,T heoretical analysis and design of the support posts in coaxial extractor of microwave source[J]. Journal of M icrowares,2004,20(2):46-50.(in Ch-i nese)

[9] 张克潜,李德杰.微波与光电子学中的电磁理论[M].第二版,北京:电子工业出版社,2001:274-276.

[10] ZAPPELLI L.On the definition of the generalized scattering matrix of a lossless radial line[J].IEEE trans.on microwave theory and techniques,2004,52 (6):1654-1662.

Mode transformation and single mode propagation condition of the radial line feeding network

LI Xiang-qiang LIU Qing-xiang ZHAO Liu ZHANGJian-qiong
(School of Physical Science and Technology, Southwest Jiaotong University,Chengdu Sichuan 610031,China)

During the design of high-power radial line array antenna,the analysis of the high mode characteristic and its controlling method are of great significance By applying mode matching to the radial waveguide,a method of analyzing the mode transformation in the radial line feeding network is proposed.Quantitative calculations on the mode transformation due to probe insertion are developed for two conditions under the aid of an analogical model. T he quantitative relation between the order of the high mode and the amount of the probes is obtained,based on which,a necessary condition for the single mode propagation in the feeding network is presented.The result shows that,in order to ensure the single mode propagation,the number of probes that can be inserted at a certain radius of the radial line is constrained by an upper limit and a lower limit,and only the middle part of the limit range can be used to determine the array arrangement in practical designs.

mode matching method;high mode;array arrangement;coupling probe;radial line

赵 柳 (1975-),女,四川人,西南交通大学讲师,博士,主要从事高功率微波技术研究。

TN81

A

1005-0388(2010)03-0553-06

李相强(1982-),男,山东人,西南交通大学讲师,博士,主要从事高功率微波技术研究。

刘庆想 (1964-),男,山东人,西南交通大学教授,博士生导师,从事高功率微波技术研究,已在国内外重要期刊发表学术论文八十余篇。

2009-08-29

中央高校基本科研业务费专项资金资助(SWJTU09ZT 38)

联系人:李相强E-mail:xiangqiang_li@163.com