二水平正交饱和设计中零效应搜索法的推广
张晓琴,赵深淼
二水平正交饱和设计中零效应搜索法的推广
张晓琴,赵深淼
(山西大学数学科学学院,山西太原030006)
文[5]中提出的零效应搜索法是分析饱和设计的有效方法.一般假定误差是服从正态分布的.零效应搜索法对于密度函数是对称分布的函数也适用,因此零效应搜索法对t分布也适用.由于t分布的密度函数比较复杂,无法给出统计量的具体形式,但可通过模拟来实现,通过对各种情况的模拟计算来说明零效应搜索法对t分布也适用.本文选择自由度为3的t分布做模拟.并且在此假定下,也能很好的识别饱和设计中的显著因子,误差方差的估计也很好.
正交饱和设计;次序统计量;零效应搜索法;显著效应;t分布
在饱和设计中,稳健设计在质量改进中有广泛的应用,研究如何正确识别显著因子的效应和估计误差方差是近年来的热点问题.已有的分析正交饱和设计的方法都是基于ε~N(0,1)假定下做的研究,如:Chen[1]提出了MaxUr方法,该方法只能识别显著因子,得不到误差方差的估计;文[2]给出的是一种逐步检验显著因子的方法,也没有给出σ的具体估计形式.而零效应搜索法在识别显著因子和估计误差方面都有很好的结果.本文在零效应搜索法的基础上,将该方法推广到t分布下做了更进一步的研究.由于t分布的密度函数比较复杂,写不出统计量的具体形式,但可通过模拟实现.
本文试验是基于2水平的因析试验.
2水平正交表Ln(2m)(m=n-1)的饱和设计通常用如下的线性统计模型来描述(详见[3]):
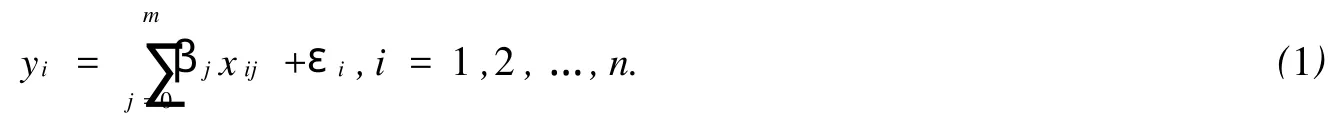
其中,β0是一般平均,β1,β2,…,βm代表因子的主效应或某些需要考察的交互效应,都是待估参数.
易见,模型(1)中β=(β0,β1,…,βm)T的最小二乘估计为:
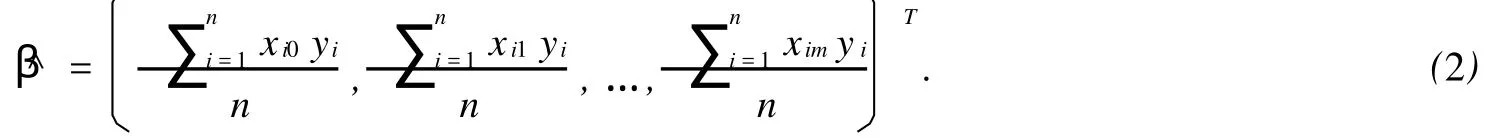
总平方和SST与各列平方和SSj(j=1,…,m)之间满足
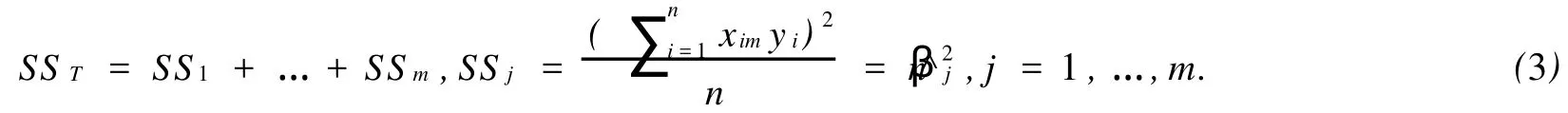
其中SST的自由度为n-1,SSj(j=1,…,m)的自由度为1.
我们的目标是,利用n个观测值y1,y2,…,yn,借助某个方法来判断,在m个效应中哪些效应是显著的.即考虑如下的假设检验问题:
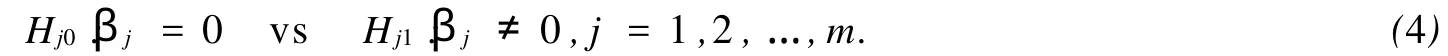
1 零效应搜索法
引理1[4]若s个随机变量X1,X2,…,Xs独立同分布,其相应的次序统计量记为:X1;s≤X2;s≤…≤Xs;s,假如它们的数学期望都存在,并记μi;s=E(Xi,s)为第i个次序统计量的期望,则有下式成立:
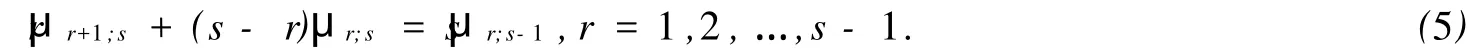
这里μr+1;s和μr;s分别表示来自总体的容量为s的样本的第r+1个和第r个次序统计量的期望,μr;s-1表示同一总体容量为s-1的样本的第r个次序统计量的期望.
分别用估计^μr+1;s=ξr+1,^μr;s=ξr,^μr;s-1=(ξr+1+ξr)/2代替μr+1;s,μr;s,μr;s-1,可得W统计量[5]如下:

零效应搜索法的步骤:
(1)首先由y1,…,yn算得^βj及SSj(1≤j≤m),算出Ws(3≤s≤m)的值.
(2)对给定的显著性水平α,我们可以按s由小到大的顺序比较每对Ws,Ws,α(3≤s≤m)的大小,若满足Ws>Ws,a的最小s=q+1,则零效应个数就是q.
2 t(3)情形下σ2的均值模拟
考虑正交表H=L16(215)对应的饱和设计模型(1),即yi=β0+β1xi1+…+β15xi,15+εi,i=1,…,16.令εi是取自t(3)的随机数,即σ2=3.我们依次假设显著因子的个数分别为1个,2个,4个,6个.1个显著因子时,取β1=size;2个显著因子时,取β1=size,β2=2size;4个显著因子时,β1=β2=size,β3=β4=2size;6个显著因子时,β1=β2=size,β3=β4=2size,β5=β6=4size;8个显著因子时,β1=β2=size,β3=β4=2size,β5=β6= 3size,β7=β8=4size;10个显著因子时,β1=β2=β3=size,β4=β5=β6=2size,β7=β8=β9=3size,β10=4size;其中size=1,2,3,4.上面所有的没有列出来的效应以及β0都等于0.对于上述的每种情况,我们利用SA S的rannor函数构造出自由度为3的t-分布,产生均值为0,方差为3的随机数.并且对每种情况都模拟计算100次,下面的表1到表6列出了每种情况下所计算出的100个σ^2的均值σ^2和标准差s.
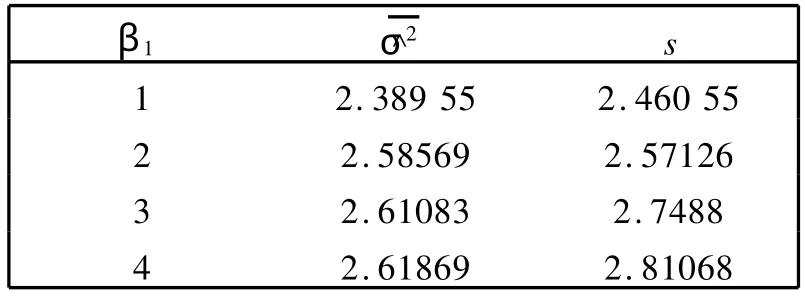
表1 1个显著因子Table 1 One significant factor

表2 2个显著因子Table 2 Two significant factors
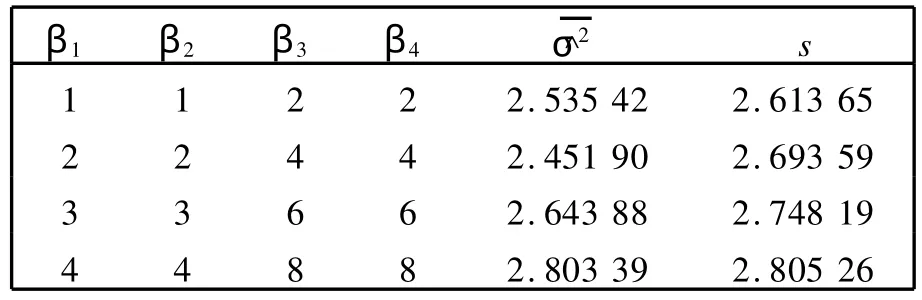
表3 4个显著因子Table 3 Four significant factors

表4 6个显著因子Table 4 Six significant factors
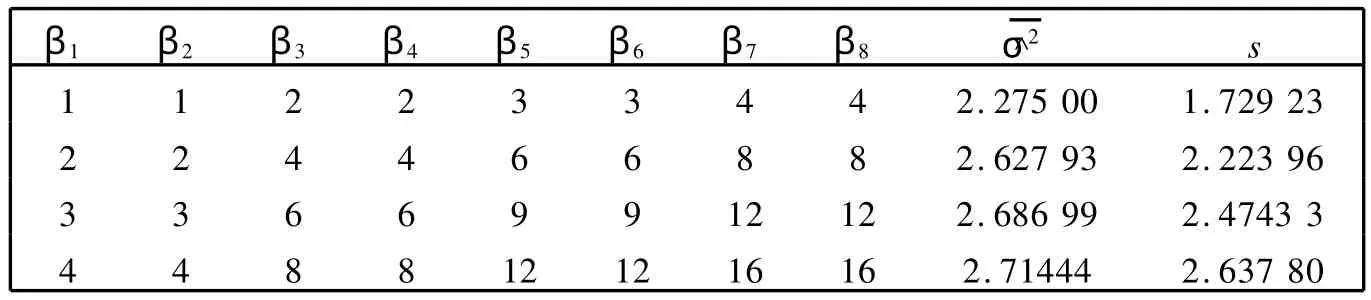
表5 8个显著因子Table 5 Eight significant factors

表6 10个显著因子Table 6 Ten significant factors
上述计算结果显示,对2水平的饱和设计而言,当所有的非零效应都大于3时,σ2的估计较好,其与真实值的偏差不超过0.38.当显著因子的效应小于3时,σ2的估计稍微偏小,这是因为我们选择的εi是取自t(3)的随机数,估计值偏小是正常的.另外,σ2的估计的标准差随着显著效应值的增大而增大,接近于目标值3.这说明我们给出的关于2水平饱和设计的误差的估计方法是一个令人满意的方法,对密度函数为对称函数的分布均适用,都能用该方法来估计,且不再需要效应稀疏原理的约束.
3 零效应搜索法对t(3)的模拟分析
例1 考虑正交表H=L16(215)对应的饱和设计模型(1),即yi=β0+β1xi1+…+β15xi,15+εi,i=1,…, 16.令εi是取自t(3)的随机数,即σ=3.又令β1=β2=2,β3=β4=4,β5=β6=6,β7=β8=8,β0=β9=…=β15= 0.而各个xij的取值情况详见引言的模型叙述.可得到如下的试验数据(y1,…,y16)=(42.703,28.768 4,-9.319 9,-23.123 8,0.407 3,-14.968 8,6.6922,-8.087 1,-0.378 7,-14.217 7,7.041 2,-7.488 0, 9.480 1,-10.480 8,7.284 2,-8.312 0).在显著性水平α=0.05下进行分析.
首先由(2)算出各个βj的最小二乘估计^βj(j=1,…,15).算出各效应平方和SSj=16^β2j(j=1,…,15),具体见表7的第3,4列.并将Ws(3≤s≤5)与其对应的临界值Ws,0.05(见附表)列于表8的第2,3列.观察发现,满足Ws>Ws,0.05的最小的s=8,从而零效应个数q=8-1=7.这与模拟前给定的零效应个数是一致的.而σ2的估计^σ2=SSe/7=(SS1;15+…+SS7;15)/7=2.627 93.即^σ=1.621 01.由q=7可初步判定最小的7个SSj;15对应的效应为零,另外的8个效应非零,即表7,表8中打*所对应的效应1,2,3,4,5,6,7,8是显著的.再由t-统计量进行验证,即计算效应1,2,3,4,5,6,7,8的t-统计量的值,见表9.又注意到在显著性水平α=0.05时,t1-0.05/2(7)=2.364 62,通过观察可见,显著效应确实为1,2,3,4,5,6,7,8.

表7 例1中^βj及SSjTable 7 ^βjandSSjin the Example 1
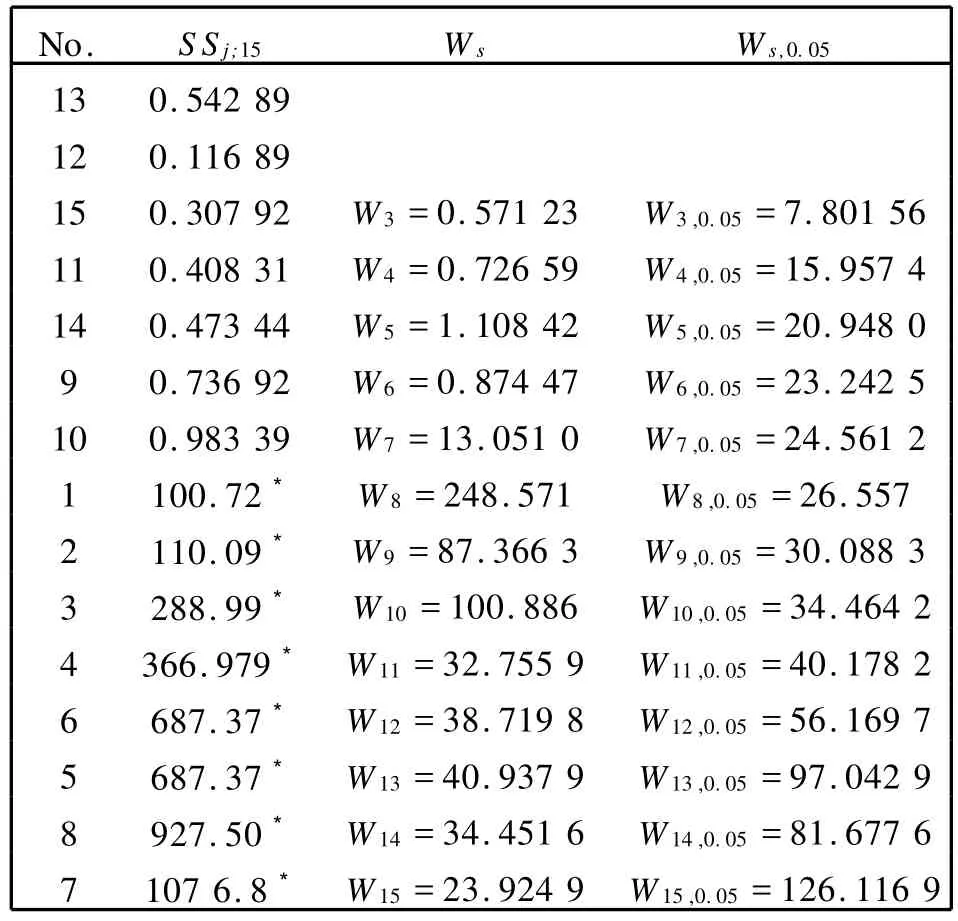
表8 例1中W统计量及其临界值Table 8 W-statistic and its critical value

表9 t-检验Table 9 t-test
另外,模拟计算1 000次的结果显示,结果如下:有527次正好选出所有真正显著的因子,有137次误将一个不显著的因子判定为显著的,80次误判2个,66次误判3个,65次误判4个,45次误判5个,80次漏判.出现漏判的原因是我们选择的ε~t(3),而随机误差的标准差是3所以可能将取值比较小的显著因子误判为零因子.这与我们选择的随机变量的分布函数是分不开的.因为t-分布的密度函数比较特殊,它的峰比标准正态分布的峰尖,尾比标准正态分布的尾更重.
4 结论
用零效应搜索法对t分布的模拟结果表明,零效应搜索法适用于密度函数是对称分布的函数.能较好的识别显著因子,且对误差方差σ2的估计结果也令人满意.
[1] CHEN Y.On the Analysis of Unreplicated Factorial Designs[J].Biometrical J ournal,2003,46:125-140.
[2] WU S S,WANG W.Step K-up Simultaneous Tests for Identifying Active Effects in Orthogonal Saturated Designs[J].A nn Statist,2007,35:449-463.
[3] 茆诗松,周纪芗,陈 颖.试验设计[M].北京:中国统计出版社,2004.
[4] KARPL J K,KAPADIA C H,OWEN D B.Handbook of Statistical Distributions[M].New York and Basel:Marcel Dekker Inc,1976.
[5] 张晓琴,张应山,茆诗松.二水平正交饱和设计的统计分析——零效应搜索法[J].华东师范大学学报(自然科学版), 2008,1:51-59.
Spread of the Procedure of Searching Zero Effects in the Statistical Analysis of 2-Level Orthogonal Saturated Designs
ZHANG Xiao-qin,ZHAO Shen-miao
(School of Mathematical Sciences,Shanxi University,Taiyuan030006,China)
The article[5]proposed the procedure of searching zero effects which is a effective method in analyzing orthogonal saturated designs.Generally,it assume that the errors are subject to normal distribution. Because the density function oft-distribution is also a symmetric distribution,the procedure of searching zero effects is also applicable to thet-distribution.The density function oft-distribution is much more complicated,so it can’t give the specific form of statistics.However,it can achieve by simulation,through the simulation of various situations,illustrate that the procedure of searching zero effects is applicable to thetdistribution.Choosing the distribution oft(3)to do the simulation,under this assumption,it can also identify significant factor in orthogonal saturated designs,and the estimated of error varianceis also very well.
orthogonal saturated designs;order statistics;Procedure of Searching Zero Effects;active effects;t-distribution
O212.1
A
0253-2395(2010)02-0182-04
2009-05-26
国家自然科学基金(44K55050);山西省高校高新技术产业化项目(20090006)
张晓琴(1975-),女,山西长治人,博士,研究方向:试验设计.E-mail:zhangxiaoqin@sxu.edu.cn

