PKP-方程的精确周期孤子解和双周期解
李自田
PKP-方程的精确周期孤子解和双周期解
李自田
(曲靖师范学院数学与信息科学学院,云南曲靖655011)
应用同宿测试方法研究并获得了PKP-方程的新的精确周期孤子解和双周期解,同时得出了该方程在点p2=4处具有衰减性.从平衡点的左侧到右侧,方程的解从周期孤子解衰变为双周期解.
周期孤子解;双周期;同宿测试法;衰减
0 引言
在过去的二十年里,在非线性发展方程广泛出现的应用领域引起了数学和物理工作者的普遍关注,许多学者在这一领域进行了卓有成效的研究.特别是在精确解的寻求和获得方面开辟和发展了许多方法.诸如, F-扩展法[1];齐次平衡法[2]以及逆散射法[3]等.

在本文中,我们将研究如下形式的PKP-方程:其中u:Rx×Ry×Rt→R.并且:取自“+”和“-”被分别称为PKP-I方程和PKP-II方程.
众所周知,该模型属于潘勒卫不可积类型.但通过应用潘勒卫扩展变换,我们可将该方程转换为双线性方程,进而通过对双线性方程的研究,可找出并获得该方程的解.
最近以来,该方程在诸多方面获得了较广泛的研究[3-6].许多学者在这些方面取得了很大的进展.文献[5]通过应用F-扩展函数的方法研究并获得了用椭圆函数表示的一系列周期波解;在文献[6]中,文章的作者给出了该系统的N-孤子解,并得出了该系统可简化为Melnikov-方程和KP-方程的特殊类型的结论.
本文通过对双线形方程的研究,应用文献[7]发展起来的方法,即同宿测试法,获得了该方程的新的周期解和双孤子解,其中的一些方法的应用和结论在解决其他同类型的问题中将具有十分深远的意义.
1 PKP-I方程的解
首先,我们考虑PKP-I方程:
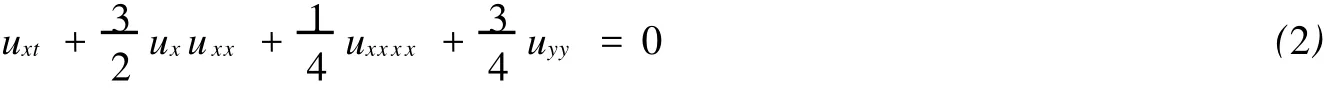
引入变换:

将(3)代入方程(2),则方程(2)可化为:

随后,我们采用下面的变换:

将变换(5)代入方程(4),则我们得到如下形式的双线性方程:

这里,算子“D”定义为:

引入测试函数:

其中b1,b2,Ω,τ,p是实数.
将(7)式代入方程(6),通过计算,我们得到如下的关系式:

从而,将(8)代入(7)并代入(5),我们得到方程的周期孤子解:

显然,我们要求条件:
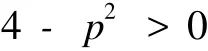
以便使式(8)中的Ω2>0,从而确保Ω能取到实数.
把ζ=x+t代入(9)中,并令b2=1.从而,我们得到下列形式的周期孤子解:

2 PKP-II方程的解
考察如下形式的PKP-II方程:

应用和上面使用的相同的变换以及处理PKP-I方程所用的类似的方法,我们有双线性方程:

设:

将(13)代入方程(12)并应用符号计算系统,我们获得了方程(11)的精确解:

其中系数满足:
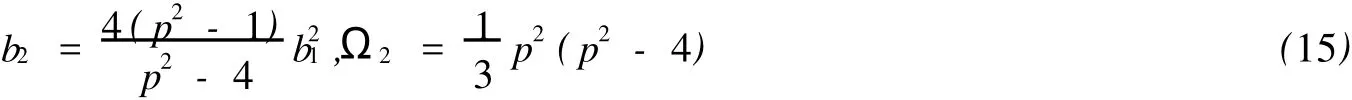
同理,要求条件:p2>4,从而使得(15)中Ω的满足Ω2>0.
类似地,我们取b2=1.则PKP-II方程的精确解具有如下表达式:

3 解的研究
考虑变换:(ζ,y)→(ζ,iy)
将它代入(9)并令τ=0.我们得到了一个新解,它是一个双周期解:

比较方程(2)和方程(11),我们不难发现,只要我们应用时间和空间的变换(ζ,y)→(ζ,iy),方程(2)可以转换为方程(11),反之亦然.这样,我们获得了PKP-I方程的双周期解:
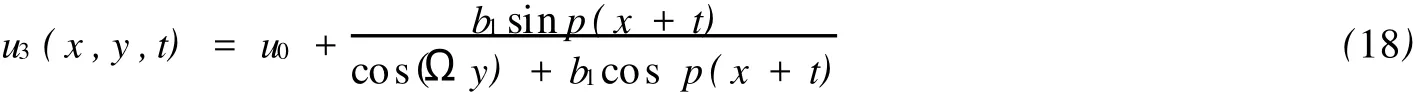
其中:p2-4>0.
注意到,(18)是PKP-I方程的奇性周期解.为了避免奇性,我们令cos(Ωy)>0和cosp(x+t)>0.
此外,同理可得PKP-II方程的双周期解:
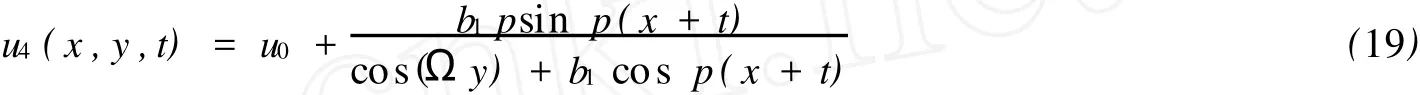
其中,要求条件:p2-4<0.
依据讨论,我们得出结论:p2=4是PKP-I方程和PKP-II方程的唯一周期分歧点.在p2=4的两侧, PKP-I方程和PKP-II方程的解的性质发生了改变.当平衡点p2从4的一侧变到另一侧,周期孤子解衰变为双周期解.
[1] ZHANG Hui-qun.New Exact Travelling Wave Solutions for Some Nonlinear Evolution Equations,Part II[J].Chaos, Solitons and Fractals,2008,37:1328-1334.
[2] ZHOU Yu-bin,WNAG Ming-liang,MIAO Tian-de.The Periodic Wave Solutions and Solitary Wave Solutions for a Class of Nonlinear Partial Differential Equations[J].Phys Lett A,2004,323(1-2):77-88.
[3] ABLOWITZ M J,CLARKSON P A.Solitons,Nonlinear Evolution Equations and Inverse Scattering Transform[M]. Cambridge University Press,1990:8-17
[4] CARIELLO F,TABOR M.Painleve Expansions for Non-integrable Evolution Equations[J].Physica D:Nonlinear Phenomena,1989,39(1):77-94.
[5] AKHMEDIEV N,ANKIEWICZ A.Solitons,Nonlinear Pulses and Beams[M].Chapman and Hall,London,1997:124-127.
[6] ZHOU Yu-bin,WANG Ming-liang.Periodic Wave Solutions to a Coupled Kdv Equations with Variable Coefficients[J]. Phys Lett A,2003,308(1):31-36.
[7] DAI Zheng-de,LI Shao-ling,ZHU Ai-jun.Singular Periodic Soliton Solutions and Resonance for the Kadomtsev-Petviashvili Equation[J].Chaos,Solitons and Fractals,2007,34(4):1148.
Exact Periodic Soliton Solution and Double Periodic Solution to PKP-equations
LI Zi-tian
(College of Mathematics and Inf ormation Science,Qujing Normal University,Qujing655011,China)
The periodic soliton and the double periodic solutions to PKP-equation are obtained by using homoclinic test method.Mean while,we also find that the equation has the properties of degeneration atp2= 4.When the equilibriumpvaries from one side ofp2=4 to the other side,the periodic soliton solution changes into a doubly periodic solution.
periodic soliton solutions;double periodic;homoclinic test method;degeneration
O175.23
A
0253-2395(2010)02-0166-03
2009-04-07
国家自然科学基金(10361007,10661002);云南省教育厅科学研究基金项目(08Y0302);曲靖师范学院科研基金(2008MS018;2009MS007)
李自田(1972-),男,硕士,讲师,主要从事偏微分方程研究.E-mail:lizitian88@163.com

