复杂氧化还原电极电极电势的计算

王芬华，黄江胜，王崇侠，陶庭先

（安徽工程大学 生物化学工程学院，安徽 芜湖241000）

复杂氧化还原电极电极电势的计算

王芬华，黄江胜，王崇侠，陶庭先

（安徽工程大学 生物化学工程学院，安徽 芜湖241000）

对复杂电极电势计算公式进行推导、归纳和比较，使学生掌握难溶盐电极在标准状态、非标准状态下的电极电势以及配合物电极电极电势的计算。

电极电势；沉淀溶解平衡；配位解离平衡

电极电势有着广泛的应用，如计算原电池电动势，判断氧化还原反应进行的方向及限度，测定难溶盐的溶度积常数和配合物稳定常数等［1－3］。由于其内容多，抽象，很多学生在学习过程中感觉很难接受。我们在无机及分析化学课程授课过程中发现，大一学生尤其对难溶盐电极、配合物电极的电极电势的计算不能理解。为此，我们在课堂上通过推导、归纳、比较等手段，帮助学生理解、消化。

一、难溶盐电极标准电极电势的计算

例1［4］已知φθ（Ag＋／Ag）＝0.799V，。求下列电极反应的φθ：

分析：《无机及分析》［4］上直接给出下面的计算式：

直接看这个表达式，学生很难理解，电极反应式中并未出现Ag＋，而电极电势中却与Ag＋浓度有关。为了帮助学生理解，在讲授过程中，我们将其设计成一组原电池，如上例中可以设计成下面的原电池反应：

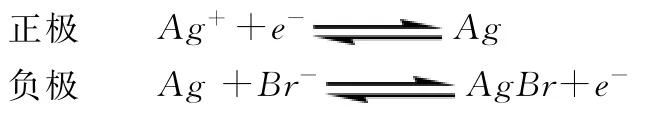
很显然，该反应的标准平衡常数

其中z＝1，将（2）、（3）式联立变形得即

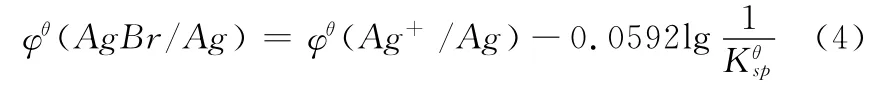
因为是在标准状态下，由于 ［Br－］＝1.0mol·L－1，所以（4）式可以变形为

通过推导，学生就可以理解上述计算式了，然后再引导学生求难溶盐电极在非标准状态下的电极电势。

二、难溶盐电极在非标准状态下电极电势的计算

我们就以例1的条件，假设［Br－］＝0.1mol·L－1，求φ（AgBr／Ag）＝？

分析：从（1），我们不难得出

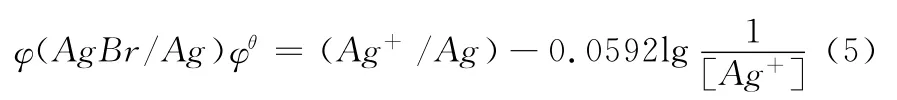
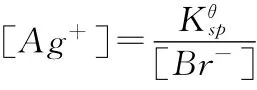
显然，电极电势就有两种不同的计算方式了，这时我们还需要推导，证明这两个式子是等同的，学生就能理解得更透彻了。

将（4）式代入（6）式得

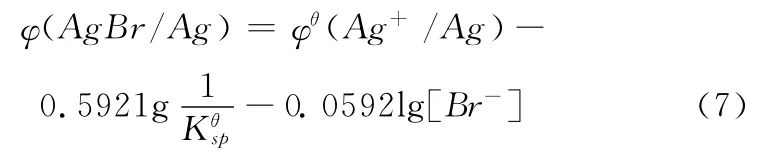
如果在非标准状态下，则电极电势可以表示为：

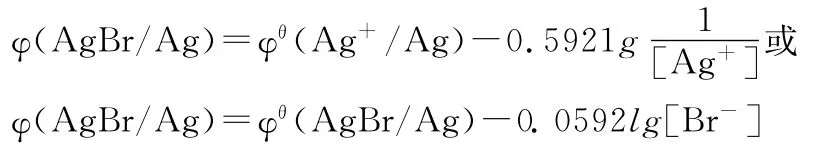
那么对于配合物电极的电极电势的计算，有了前面的基础，学生就很容易接受了。

三、配合物电极的电极电势的计算

对于配合物电极的电极电势可以给出一个例子，先让学生自己推导，老师再作总结。

例2［4］已知，φθ＝－0.763V，，求算的φθ

分析 该例子同样可以设计成下面两个半反应：

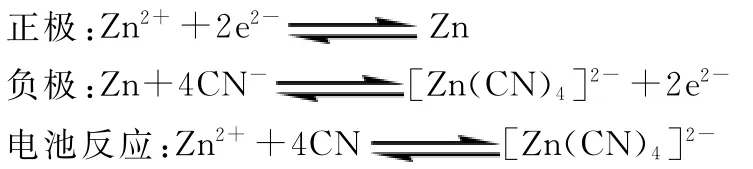
同理，此反应的标准平衡常数

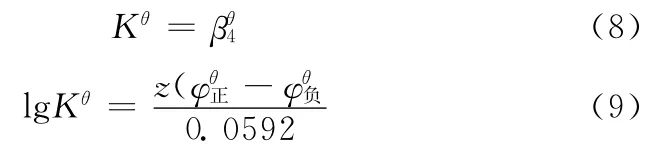
其中，z＝2。联立（8）、（9）两式，即可得到

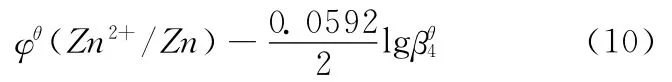
因为是在标准状态下，所以

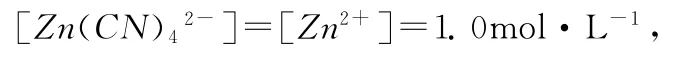
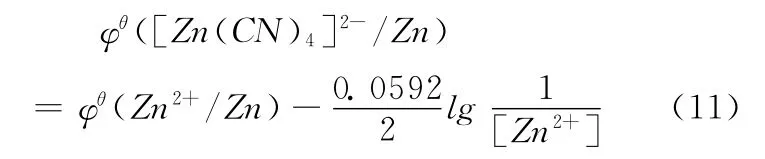
也就是说φθ（［Zn（CN）4］2－／Zn）可以用（10）或 （11）式表达。

通过前面两个例子的讲解和公式推导以及配合物电极电势计算的巩固，学生对这方面的知识就容易理解和接受了。

［1］马志领，李志林.无机及分析化学［M］.北京：化学工业出版社，2007.

［2］浙江大学.无机及分析化学［M］.北京：高等教育出版社，2003.

［3］陈虹锦.无机及分析化学［M］.北京：科学出版社，2002.

［4］南京大学无机及分析编写组.无机及分析［M］.（第四版）.北京：高等教育出版社，2006.

G642.4

：A

：1673－1794（2010）05－0121－02

王芬华（1979－），女，硕士，讲师，主要担任无机及分析化学课程的教学与研究。

安徽工程大学教学研究项目（2009jyy29）

2010－07－11