价层电子对互斥理论和应用

吴 刚，冯 剑，愈 力

（滁州学院 化学和生命科学系，安徽 滁州239012）

价层电子对互斥理论和应用

吴 刚，冯 剑，愈 力

（滁州学院 化学和生命科学系，安徽 滁州239012）

价层电子对互斥理论是判断和预见分子形状的有力工具，认为分子的形状是由价层电子对域的分布决定的，本文介绍价层电子对互斥理论和演变，讨论了孤对电子、电负性和多重键对分子形状的影响。

价层电子对互斥理论；域；电负性；多重键；孤对电子

1 介绍

在无机化学和结构化学教学中，预见分子的形状对学生和老师来说，都是比较困难的，常见的有杂化轨道理论、分子轨道理论和价层电子对互斥理论，由于价层电子对互斥理论模型比较简单，特别对主族元素化合物的空间形状有比较好的预见性，常被用来解释分子的形状。

1874年Le Bel和van＇t Hoff各自独立的提出碳4价的四面体学说，开始出现立体化学，通过这个模型，人们能够解释分子的手性，这个模型后来被扩展到无机化学来解释4配位的Si、B的离子如，N的离子如。后来，Werner提出6配位的过渡金属化合物的分子和离子具有八面体构型，并通过分子的光学异构体而得到证明。随着X－射线的应用、红外光谱、拉曼光谱的应用，这些假释都证明是正确的。

1940年，物理学家Sidgwick、Powell通过对AXn分子形状的研究，认为分子的形状是由中心原子A价层中的成键和非键的电子对总数决定的，他们得出结论，价层电子对是2的时候，是线形排列，3的时候是三角形排列，4的时候是四面体排列，5的时候是三角双锥排列。但是这个重要思想在当时没有得到重视，直到1957年Gillespie和Nyholm发展和扩展了这个思想，变成了价层电子对模型（valence shell electron pair repulsion model：VSEPR），他们发现，很多分子，尤其是主族元素的分子结构是和Sidgwick、Powell的提议是符合的，发现由于保里原理的作用，电子对尽可能离远一些。后来，特别是Gillespie的努力，该模型发展演变成今天的价层电子对互斥理论（也叫做Gillespie和Nyholm 规则）［1］。

价层电子对互斥理论的基本假设是电子对采取尽可能远的排布，表现的好象互相排斥。我们首先考虑价电子层含有8个电子的情况，4个顺时针自旋，4个逆时针自旋，4个相同自旋的电子离得愈远愈好，位于四面体的顶点上（图1），因此有两套自旋交替地排列在立方体的顶点上，但是由于电子的排列没有固定的方向，因此总的电子分布是球形的，有趣的是，开始时，Lewis提出八隅体中8个电子是立方体排列，后来废弃了这种想法，而提出4对电子四面体排列的模型，对于自由原子或者离子而言，总的电子分布是球形的是正确的，如果将α和β自旋电子配对，就可以形成四面体，四面体的每个顶点是有1对电子［1］。

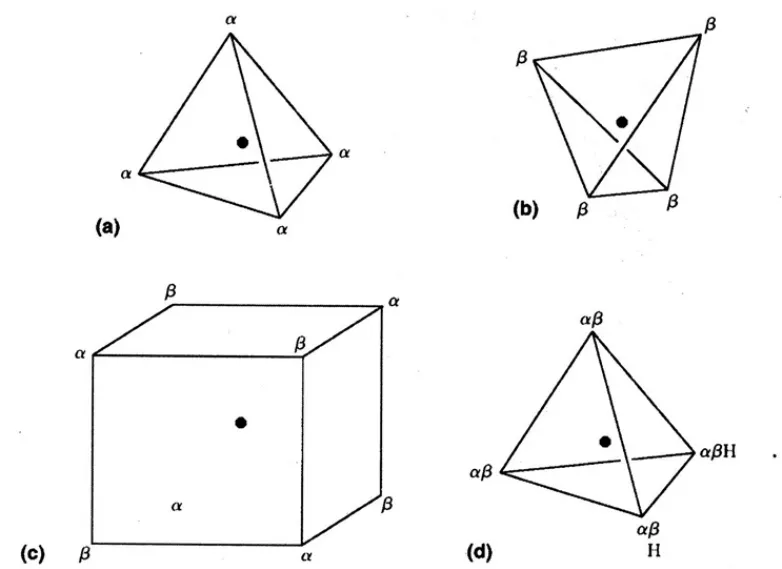
图1 最可能的排列

分子中电子的球形分布受到了和它联结的其它原子的扰动，例如，H2O分子，O2－离子和2个质子结合形成H2O分子，仅仅2个自旋相反的电子可以被质子同时吸引在周围，四面体的电子和电子被吸引配对，形成四对，因此四对电子不再是球形的排列而是四面体排列了（图2），但是对于没有和其它原子形成键的电子对，其运动的范围要大得多，例如HF分子中没有和氢原子联结的3对电子，均匀分布在环上（图3）［1］。

在使用该理论判断化合物的几何构型时，第一步要计算出中心原子的价层电子对数，首先确定价层电子的空间排布，然后才能确定分子的形状。

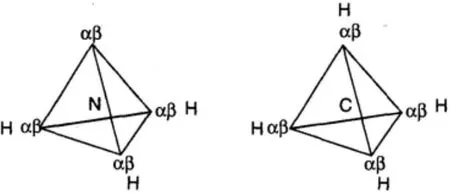
图2 NH3和CH4分子中4个αβ自序电子对的排列

图3 HF分子中价层电子的最可能排列，仅形成1对定域电子对，其它电子均匀分布在环上，· 代表α电子，°4代表β电子

表1 价层电子对的排布方式和电子对数的关系

在上面的讨论中，是将电子对作为一个点，但我们知道电子运动有个范围，为了解决这个问题，Gillespie提出了域的概念。所谓域可以定义为发现电子对可能性高的空间或者发现较大部分电子对电子云的空间。电子对域包围着电子云密度最大的点，因此在水分子中存在4个电子对域，2个成键的域，2个非键的域，以四面体形式排列。对于电子域的分布，先后提出了下列模型，这几个模型现在也在使用：

1.点在球上的模型：这些域可以简化为点，这些点分布在球面上，分离的尽可能远，即“点在球表面模型”（points－on－a－sphere－model，图4），此模型被使用最多。

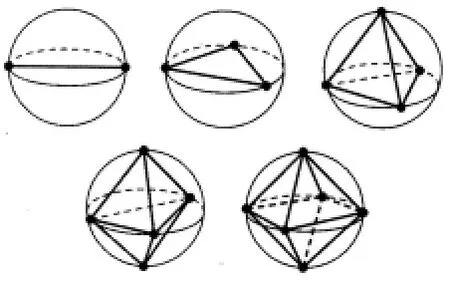
图4 点在球上的模型，在球上距离最远时，2、3、4、5、6对电子时的最可能排列

2.球表面上的圆环模型（circles－on－a－sphere－model）

图5 球表面上的圆环模型

3.相切球模型（tangent sphere model）

图6 相切球模型

由于电子对领具有一定的伸展方向，每个电子对域沿着最大伸展方向和另外的原子成键，因此化学键也有方向性，所以分子具有一定的形状，分子的形状是由价电子对的域决定的。下面是价电子对是2、3、4时的电子对域分布情况。

图7 电子对是2、3、4时的电子对域，A表示成键电子对，E表示孤对电子对

表1是中心原子各种电子对域时的分子形状的具体例子。

表2 电子对排布和AXnEm分子的几何形状

图8 价层电子对为2－6时的分子形状

从表2和图8可以看出，只有当孤对电子数等于零时，价层电子对的形状才和分子的形状一致。下面讨论影响分子形状的因素。

2 影响分子形状的因素

2.1 孤对电子对分子形状的影响

价层电子对斥力之间存在斥力，当斥力大小改变的时候，会影响键角的大小，进而影响分子的形状。价层电子对之间斥力大小顺序是：

孤对电子－孤对电子＞孤对电子－成键电子＞成键电子－成键电子

如在NH3分子中（图9），非键电子对由于只受到中心原子的吸引，和受到2个原子吸引的成键电子对相比较，其伸展空间较大，因此成键电子对受到挤压，其键角小于理想的四面体角度。孤对电子对数愈多，其影响愈大（图10）［1］。

图9 NH3分子中成键电子对域和非键电子对域的相互排斥

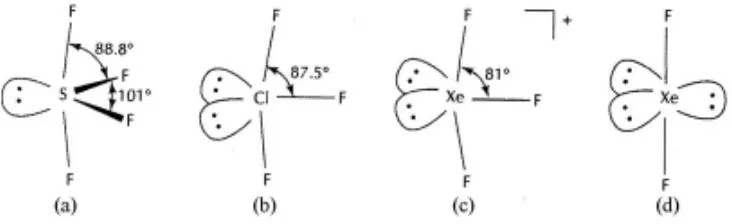
图10 孤对电子对数对键角的影响

2.2 电负性对键角的影响

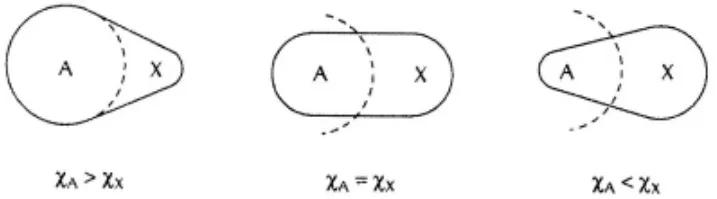
图11 电负性对键角大小的影响

如果配体的电负性比中心原子大，中心原子价层的成键域电子密度受到配体的吸引而下降，并且差愈大，下降的愈多，导致轨道收缩愈大，键对愈靠近配体，相邻轨道斥力减小，导致键角变小，例如PI3中，键角是102°，而在PF3中，键角是97.8°，反过来，如果中心原子电负性愈大，则键角愈大，PBr3键角是101.5°，而 AsBr3键角是99.7°［2］。

2.3 多重键对键角的影响

图12 多重键对键角的影响

多重键中存在多对电子，因此对别的电子对能够产生较大的斥力和挤压，使得电子对之间夹角变小，对键角产生影响（图12），从而影响分子的形状，斥力大小顺序是：

在有双键的三角双锥形状的分子中，双键总是占据着较不拥挤的三角双锥的赤道位置（图13）。

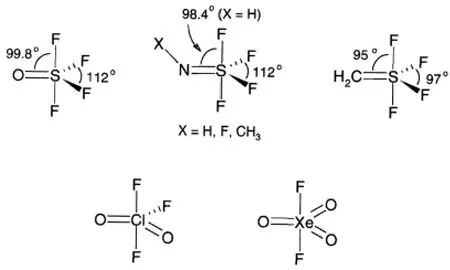
图13 双键占据着较不拥挤的三角双锥的赤道位置

VSEPR理论可以用来解释和预见许多主族元素的化合物的立体结构，对于具有d0，d10和高自旋的d5电子结构的过渡金属元素的化合物可以和主族元素一样，可以用价层电子对互斥理论预见其几何构型，但也存在例外：例如 N（CH3）3，O（CH3）3，OCl2的键角大于109.5°，价层电子对理论不能解释；另外过渡金属化合物的结构除了具有d0，d10电子结构和d5高自旋的化合物外［3］，其它化合物分子形状不能用价层电子对理论解释。

［1］Gillespie RJ，Popelier PLA.Chemical Bonding and Molecular Geometry From Lewis to Electron Densities［M］.New York：Oxford University Press，2001.

［2］陈彗兰，余宝源.理论无机化学［J］.北京：高等教育出版社，1985，2：57－58.

［3］U.Muller，Inorganic Structural Chemistry（Second Edition）Muller U［M］.England：John Wiley ＆Sons Ltd，1992：62.

Valence Shell Electron Pairs Repulsion Theory and its Application

Wu Gang，Feng Jian，Yu Li
（Department of Chemistry and Life Sciences，Chouzhu University，Chuzhou 239012，China）

Valence shell electron pairs repulsion theory（VSEPR）is a powerful means of measuring and predicting a molecular shape，which is determined by distribution of electron domains according to it.This article discusses the VSEPR theory，its evolvement and the impacts of lone－pair electron，electronegativity and multiple bonds on a molecular shape.

VSEPR theory；domain；electronegativity；multiple bonds；lone－pair electron

O611.2

：A

：1673－1794（2010）05－0108－03

吴 刚（1963－），男，博士，副教授；研究方向：配位化学，生物无机化学。

安徽省应用化学重点学科（200802187C）

2010－07－11