《容积和容积单位》教学设计与分析
马顺红
教学目标:
1.知道容积的含义,理解体积和容积之间的联系与区别。
2.认识常用的容积单位升与毫升,初步建立升与毫升的容积观念。
3.培养观察、独立思考和应用几何基础知识解决实际问题的能力。
教学重、难点:知道容积的含义,掌握容积单位间的进率;量(升、毫升)感的培养。
教学预设:
一、建立容积的概念
(一)复习旧知
引领:先说说自己对“体积”概念的理解;接着说一说长方体(立方体)体积的计算方法。
【分析:新授前先复习学生已有的对体积概念的理解与长方体体积计算方法,有助于在新课中更好地理解容积的概念并很好的与之相区分。再者,长方体容器的容积计算方法与它的体积计算方法一致,只是数据区别,所以在这里做一简短的回顾,为突破容积的重难点教学埋下伏笔。】
(二)认识容积
1.出示长方体集装箱图片:

问题:这是一个长方体集装箱,它的主要用途是什么?集装箱为什么就可以用来装货呢?(因为集装箱里面是空的)是啊!它里面包含着一定的空间,有了这个空间它就能容纳物体。(强调并板书:能容纳物体。)
2.出示规格:从外面量长12.2米,宽2.4米,高2.6米;从里面量,长11.8米,宽2.1米,高2.2米。)
结合已有的知识与信息,你还能知道这个集装箱的哪些信息?
生1:可以知道做这样一个集装箱的一共需要的钢板材料,就是求它的表面积,用外面的尺寸数据。
生2:我们还能知道整个集装箱到底有多大,就是求它的体积,也用外面的尺寸数据来计算。(12.2×2.4×2.6=76.128立方米。)
师:既然集装箱是用来装货的,那么它能不能容纳下体积是76.128立方米的货呢?为什么?
生3:肯定不能。集装箱材料存在着一定厚度,里面的空间肯定要比它的体积小些,所以我认为不能容纳下体积是76.128立方米的货。(学生鼓掌)
师:要知道这个集装箱里面的空间到底有多大或者说它到底能容纳下多大体积的货,有办法知道吗?(11.8×2.1×2.2=54.516立方米)
小结:现在我们知道了,这个集装箱最多能容纳下体积是54.516立方米的货,我们就把54.516立方米叫做这个集装箱的容积。(板书:容积)
【分析:通过引导学生认识、了解集装箱,让学生在自我争辩中不仅认识容积的含义,同时也在不经意中区别了体积与容积的意义,是一个很典型很贴切的学习材料。】
3.思维拓展
问题1:以这个长方体集装箱为例,它的体积和容积之间有什么联系和区别?什么情况下物体的体积和它的容积更接近?
问题2:生活中你还见过哪些物体像集装箱、仓库一样能容纳物体,有容积?(学生举例:水桶、油箱、抽屉…)
小结:我们把像水桶、油箱、抽屉、仓库……所能容纳物体的体积叫做它们的容积。计量容积,一般就用体积单位。
【分析:通过教师进一步的设问,以及对具有容积物体的举例,使学生把新认识的容积与原来认识的体积进行了再次深入比较,有助于加深对容积含义的理解,使容积的表象在学生头脑中的建立更加清晰、明朗化。】
二、培养升、毫升的量感
(一)认识容量单位升、毫升
1.引出容量单位
引导学生观察课前准备的装过牛奶等液体的瓶子或包装盒的标签纸。想一想:里面曾经装着多少量的液体?在学生的汇报中因出液体容量的计量单位:升(L)和毫升(ml)。
找一找,记一记:常见的1瓶矿泉水是几毫升?常见的大瓶装雪碧又是多少升?
【分析:引导学生观察装过液体的标签,使学生自主发现计量液体多少常用升和毫升做单位,有助于学生更好地理解容量单位。并让学生识记常见矿泉水与大瓶装雪碧的容量,有助于在后续学习中估计其他装液体的容量时可以以此为参照标准去估计,比如去估计桶装色拉油的容量会更有方法、更准确。】
(二)建立1升、1毫升的量感
1.建立1升的概念
出示:一瓶容量正好是1升的红酒。
实验1:平时喝水经常用到一次性杯子,那么这里的1升红酒大概能倒满几杯呢?先猜想再实践。(实验后提问:现在请你告诉大家1升水到底有多少?)
实验2:我们已经知道了计量液体的多少总是用升和毫升来做单位,那么升和毫升又有着怎样的关系呢?(出示量杯,上面标着刻度,最高标着200毫升。)得出:1升=1000毫升
【此前学生都知道或者无法描述1升到底有多少,通过学习我们如何去实现使得学生容易描述1升的量呢?为此,我们借助生活中正好装有1升的红酒,倒入平时常见的纸杯,大约4杯,初步建立1升的量感。再把这1升的红酒倒入量杯,测得1升与1毫升之间的关系,借助实验并非简单告知,更有利于学生接受新知、理解关系、积累经验。】
2.建立1毫升的概念
学到这里我们相信大家对1升有多少已经有了一定的感觉。那么1毫升到底有多少呢?这是1支10毫升装的双黄连口服液,想象一下,把1毫升提取出来的话,会给人一个怎样的感觉?
请一生上台,用手掌托起“1毫升”的水,用一个词形容?虽然1毫升很少,但如果我们全校近2000学生每人浪费一毫升水,有多少?全中国13亿人口呢?那肯定会是一个惊人的数字,我国水资源紧缺,尤其是目前西南干旱严重,希望大家平时能节约用水。俗话说:点滴虽小节约事大。
【在“1毫升”的教学环节,笔者更侧重让学生感知1毫升量是比较少的,也为续练习“填合适的单位”做好铺垫。1毫升的水对个体来说虽是小事,对大众来说确是大事,以此培养学生的节约意识。】
3.小结
刚才我们认识了容积单位“升”和“毫升”,知道可以分别用字母“L”和“mL”来表示。生活中,一般物体的容积常用“立方米、立方分米、立方厘米”等做单位,而计量液体的多少,如牛奶、果汁、油等,常用毫升、升做单位。
4.练笔:
①填上合适的容积单位。(课本P.53第3题)
一瓶墨水约50();一桶色拉油约5();“神州五号”载人航天飞船返回舱的容积约为6()。
②课本P.53第4题。
2.5L=ml600ml=L
3.25L=ml 450ml=L
三、解决问题(不规则物体的容积和体积测定。)
1.测定不规则物体的容积
这个瓶子有容积吗?(有)可是标签纸已经不在了,那么你有办法知道这个瓶子的容积吗?
先灌满水(沙),然后倒入量杯,读出刻度。
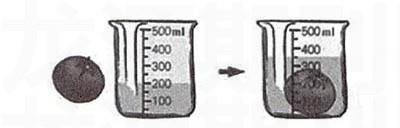
2.测定不规则物体的体积
1)准备一个能放入西红柿的量杯,倒入( )mL的水;
2)把西红柿轻轻存入水中,此时水面的刻度是 ( )mL。
3)西红柿的体积就是水面上升那部分水的体积,也就是前后水面刻度差( )Ml,即( )cm3。
【通过测定不规则物体的容积与体积,在一定程度上为学生积累基本的活动经验,同时也拓展了学生的思维空间,拓宽了知识面。】
四、总结回顾
今天我们一起学习了什么?还有什么疑问?

