双层预应力网壳在阶跃荷载作用下的动力稳定性分析

孙庆巍 辽宁工程技术大学建筑与工程学院建筑工程系 123000

双层预应力网壳在阶跃荷载作用下的动力稳定性分析

孙庆巍 辽宁工程技术大学建筑与工程学院建筑工程系 123000

文章探讨了双层预应力网壳结构在阶跃荷载作用下动力稳定性临界荷载的判别准则和方法，并以具有实际工程意义的双层肋环斜杆型球面预应力网壳为研究对象，验证了上述方法的实用性，指出其工程意义。

双层预应力网壳；阶跃荷载；动力稳定性

1、引言

预应力网壳结构是把现代预应力技术和网壳结构相结合从而形成一类新型的、杂交的预应力大跨度空间钢结构体系。目前有关网壳这种结构形式在静力作用下的稳定性问题已经研究得比较深入全面，但对这类结构在地震等动力作用下稳定性的研究仍不够深入。而且现在国内外学者比较关注的是单层网壳的动力失稳问题，对双层网壳的稳定性研究还不多见，尤其是对引入了预应力技术的双层预应力网壳更是很少提及。我国现行的网壳结构技术规程已明确指出，跨度较大、厚度较薄的双层网壳同样存在失稳的可能性。上个世纪90年代，我国双层预应力网壳结构的建设迎来了一个高峰，以1994年9月建成的四川省攀枝花体育馆为代表的十余座双层预应力网壳结构的建成与使用[1]，极大的推进了这种新型结构形式的发展，所以对双层预应力网壳结构的动力性能研究更早已提上日程。

从实用的角度，研究者自然对地震作用下的稳定性问题最感兴趣，但地震作用是一种极其复杂的荷载，预应力网壳又是一种非常复杂的空间结构，所以预应力网壳结构在地震荷载作用下的动力稳定性问题的研究难度较大。因而从人们认识事物从简单到复杂的规律来说，以阶跃荷载等相对简单的动力作用作为循序渐进的研究步骤受到充分的关注。

2、阶跃荷载作用下结构动力稳定性的理论分析

2.1 阶跃荷载的研究意义

阶跃荷载是一种幅值不随时间变化的最简单的动力荷载，由于该荷载瞬时作用于结构，会激起结构的动力响应，因此又称突加荷载。结构在该类荷载下的动力性能反映了结构抗扰动的能力，所以研究阶跃荷载作用下结构的动力稳定性对研究结构在其它复杂荷载如风荷载和地震作用下的动力响应规律有重要的参考价值，现在在结构动力稳定性分析领域中影响非常大的B-R准则就是著名学者Budiansky和Roth在研究球面扁壳结构在阶跃荷载作用下的对称屈曲问题时提出的，目前已广泛的用于研究结构在各种荷载作用下的动力稳定分析问题。另外，在阶跃荷载每一阶跃值的作用时间范围内，其荷载值又不随时间发生变化，所以，该类荷载对结构的影响，与静载相比会有或多或少的联系，这又为人们由认识结构的静力性能到动力性能提供了联系的桥梁[2]。

2.2 Budiansky-Roth准则

B-R准则也称为系统响应准则，该准则把荷载微小的变化导致结构位移突然增大时的荷载定义为动力稳定性临界荷载[3]。它的本质是Lyapunov意义上的运动失稳。B-R准则有较大的影响，它不仅适用于保守系统，也适用与非保守系统，对于屈曲后分枝路径为稳定的结构，由系统运动方程解出的位移和荷载的关系曲线单调增长而无极大值。此时，只要在加载过程中，如果该曲线上出现拐点且拐点足够明显，Budiansky建议把曲线的拐点作为动力屈曲的临界点。本文在动力稳定性分析中即采用BR准则来确定结构的临界荷载。

网壳结构是一种非线性程度极高的大型复杂结构，研究该结构的动力稳定性，其非线性问题显得更为突出，目前国际通用的大型有限元计算软件ANSYS已经能够较好的解决结构的材料非线性及几何非线性问题，其技术水平已达到国际先进水平。本文就是利用ANSYS软件先进的技术手段来研究双层预应力网壳结构的动力稳定性能。

2.3 基于B-R准则的全过程分析法

采用逐级加载的方式，对应每一荷载值作一次动力非线性时程分析，记录结构特征响应；用ANSYS软件可得出荷载作用下结构最大位移点的时程曲线，通过时程曲线可找出在这一荷载值作用下该点的最大位移。然后绘制荷载值与结构特征响应（结构位移）之间的关系曲线；通过该曲线可以全面了解结构随荷载值增大其动力性状不断变化乃至发生动力破坏的全过程。结构的动力极限荷载就以这一全过程曲线为基础来确定。根据B—R准则，我们把荷载微小的变化导致结构位移突然增加时的荷载定义为临界荷载。表现在荷载幅值与结构位移之间的关系曲线上，当荷载幅值逐步增大导致结构发生动力失稳时，单调增长的曲线上会出现拐点，说明此时在荷载增值不大的情况下，结构的位移显著增大，只要该曲线的拐点足够明显，我们就可以把曲线的拐点作为结构动力失稳的临界点，其对应的荷载即为结构动力失稳的临界荷载[4]。

3、阶跃荷载作用下双层预应力网壳结构的动力稳定性分析实例

下面即采用上文中提出的全过程分析法研究双层预应力网壳在施加竖向阶跃荷载作用下的动力稳定性。预应力网壳的结构参数为：跨度60m，矢跨比1/7.5，网壳厚度1.8m，采用沿支座两两相间布索方案。如下图：

图1 支座间两两相间预加应力体系

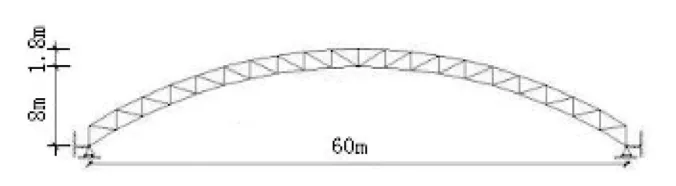
图2 预应力网壳模型剖面图

下面以逐级加载的方式对该网壳结构在竖向阶跃荷载作用下的动力稳定性进行计算分析，结果如下：

图3 荷载为0.2g时的时程曲线

图4 荷载为0.4g时的时程曲线

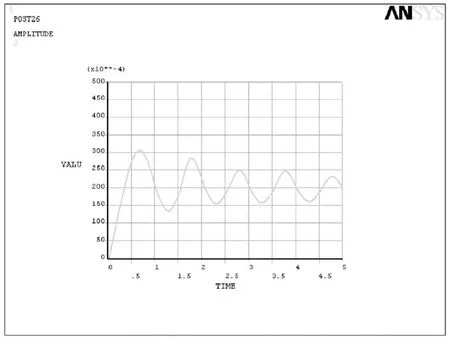
图5 荷载为0.8g时的时程曲线

图6 荷载为1.6g时的时程曲线

图7 荷载为1.8g时的时程曲线

图8 荷载为1.9g时的时程曲线

把上面的分析结果绘制成荷载值与结构最大位移之间的关系曲线,见下图：

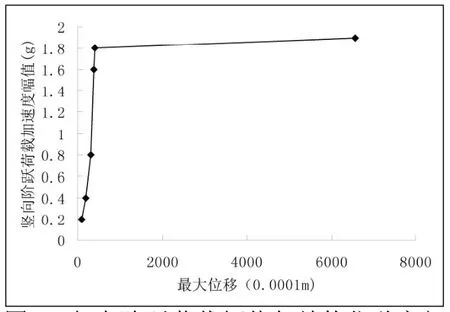
图9 竖向阶跃荷载幅值与结构位移之间的关系曲线图

从上面图中我们可以看到：在荷载幅值与结构位移之间的关系曲线中在1.8g到1.9g之间存在一个明显的拐点，1.8g之前位移随荷载幅值的增加而加大，大致呈线性变化，当荷载幅值达到1.9g时，结构位移激增，说明此时结构已发生失稳，根据B—R准则，我们得出结论，结构在竖向阶跃荷载作用下的临界荷载为1.8g到1.9g之间，可取1.85g作为临界荷载第一次近似值，要想得到更高的精度，只要在其附近增加计算点，绘制出更圆滑的曲线就可以取得更精确的临界荷载值。实际上在工程应用中，一轮次或两轮次即已满足精度要求。

4、结论

（1）针对目前对于网壳结构动力稳定性研究大都集中于单层网壳而忽视双层预应力网壳结构动力稳定性的研究这一现状，提出研究双层预应力网壳结构动力稳定性的必要性。

（2）提出应用“B—R准则”和直接基于结构受荷全过程动力响应分析的时程分析法来确定双层预应力网壳结构动力失稳的临界荷载。

（3）利用文中提出的全过程分析法（时程分析法）研究了双层肋环斜杆型预应力网壳在施加竖向阶跃荷载作用下预应力网壳结构的动力稳定性，通过ANSYS软件的建模和计算，验证了这种方法的可行性。

[1] 陆赐麟，尹思明，刘锡良.现代预应力钢结构[M] .第1版.北京：人民交通出版社.2003；17—20

[2] 周峰.单层球面网壳结构在简单荷载作用下的动力破坏机理研究[D].哈尔滨工业大学硕士学位论文.2005；5—6

[3] 郭海山，沈世钊.单层网壳结构动力稳定性分析方法[J].建筑结构学报.2003;24（3）；1—9，

[4] 郭海山，钱宏亮，沈世钊.地震作用下单层球面网壳结构的动力稳定性[J].地震工程与工程振动.2003;23（1）；31—37

10.3969/j.issn.1001-8972.2010.14.033

辽宁工程技术大学校优秀青年科学研究基金资助项目(07A118)

孙庆巍（1977—），男，辽宁阜新人，讲师，硕士，研究方向：结构振动控制。