固体热容两种物理模型的分析和比较
宋学丽
(锡林郭勒职业技术学院 机械与电力工程系,内蒙古 锡盟 026000)
固体热容两种物理模型的分析和比较
宋学丽
(锡林郭勒职业技术学院 机械与电力工程系,内蒙古 锡盟 026000)
固体热容是反映晶体热学性质的一个重要物理量,对固体热容的具体求解是一个相当复杂的问题,在一般讨论中,常采用爱因斯坦模型及德拜模型.其实验结果的理论解释是贯穿整个统计物理学的一个重要问题,由于假设模型的不同导致所得的结果各自有自己不同的特点.分别针对两种模型在高温和低温时的特点进行分析和讨论,并把两种模型进行对比,分析理论与实验出现差异的原因.对进一步理解两种模型的物理思想,及其讨论具体问题的方法具有重要意义.
爱因斯坦模型;德拜模型;固体热容;金属固体
1 引言
固体热容的实验结果的理论解释是贯穿整个统计物理的一个重要问题,通过对爱因斯坦模型和德拜模型进行理论计算所得结果的分析,爱因斯坦模型和德拜模型分别在高温和低温时表现出各自的特点.按照经典玻尔兹曼统计定容热容量为3Nk恒量[1-3].而实验上当低温时却趋于零.爱因斯坦模型和德拜模型在高温时都与实验结果一致,但低温时爱因斯坦模型趋于零的速度过快,而德拜模型在低温时以 的方式趋于零的结果与实验符合的很好.通过对两种模型的对比可以对固体热容有更深的认识.

图1 低温下晶格比热下降
2 两种模型固体热容的理论计算
2.1 爱因斯坦模型
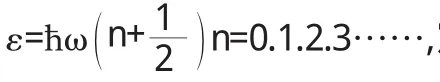

内能

热容

令

(1)当高温时,T>>θE,CV=3 NK这个结果与经典所得的结果是一致的.
(2)当低温时

结果与实验定性相符,但是在定量上符合的不好.
2.2 德拜模型
德拜模型[4,5,7]认为,固体是各向同性的连续弹性介质,固体中的原子或离子集体微振动,在固体中形成了各种频率与波矢量k的弹性驻波,整个固体的热振动能量为各种弹性驻波的能量之和,即

在固体中原子产生的弹性驻波属于声波,因此声波场的能量也是量子化的,以hv为单位增减能量,我们把声波场能量的最小单位叫‘声子’[8],可以把声子看成粒子,但又不同与真实粒子,所以称为准粒子.声子的能量和动量分别为ε=hv,p=hk对应的弹性波可分为纵波与横波,横波有两个分量代表两个偏振方向,纵波与横波波速不同,因此声子可分为纵波声子与横波声子,能量和动量的关系分别为E=clp,E=ctp,在简谐近似下,各种弹性驻波是相互独立的,所以各种频率的声子之间没有相互作用,且处在某一状态的声子数是任意的,所以声子是理想的玻色气体,由于声子可以不断产生和消灭,所以声子数不守恒,即声子气体的化学势为零.于是温度为T时处在能量为hv的一个量子态的平均声子数为

由此可知,温度为T时的内能为

其中Φ0表示所有原子都位于平衡位置时原子之间的相互作用势能,上式中第二项为声子的总能量,即温度为T时固体热运动的能量.
因此在体积v内,频率在v-v+dv之间的声子(包括纵波声子和横波声子)的量子态数为

由于固体中有N个原子或离子,共3 N个自由度,相应的有3 N的独立的弹性驻波,即声子的量子态总数为3 N,于是有

因此

其中

固体内能可表示为

即

令

于是有


其中



这正是经典玻尔滋曼统计理论所推出的能均分定理的结果.
(2)低温极限[6]:T<<θD,
则有
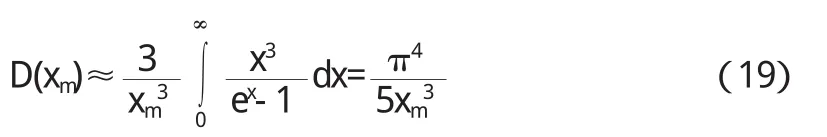
U=U0+3 Nk·

上式称为T3定律.
3 两种模型的比较以及出现差异的原因
两种热容量各有不同的特征,爱因斯坦模型高温时符合实验(CV=3 Nk),低温时热容趋于零的速度过快,是定性相符,定量符合的不好.原因是爱因斯坦模型认为所有谐振子都取同一频率太简化了.
德拜模型高温时符合实验(CV=3 Nk),低温时符合T3律,对于金属固体德拜模型在3 K以下不符,原因是3 K以下电子对热容的贡献不可忽略.
图中画出了爱因斯坦理论(虚线),德拜理论(实线),和铜的实验结果(圆圈),以作比较.

图2 铜热容的实验数据与爱因斯坦模型和德拜模型理论值的比较
固体中真实的粒子是原子,由于原子间的强烈相互作用,如果直接去处理他们,问题会变得很复杂,德拜在引入声子[8]概念后,使得模型十分形象,问题也大为简化,目前这种准粒子的方法已成为处理耦合着的多粒子系统的很有效的方法.
〔1〕汪志诚.热力学统计物理[M].北京.高等教育出版社,1980.
〔2〕马本坤,高尚惠.热力学与统计物理[M].北京.高等教育出版社,1986.
〔3〕梁希侠,班士良.统计热力学[M].内蒙古:内蒙古出版社,2001.
〔4〕黄昆,韩汝琦.固体物理学[M].北京:高等教育出版社,2005.
〔5〕王矜奉.固体物理学教程[M].济南:山东大学出版社,1999.
〔6〕王矜奉,范希会,张承琚.固体物理概念和习题指导[M].济南:山东大学出版社,2005.
〔7〕方俊鑫,陆栋.固体物理学[M].上海科学技术出版社,1980.
〔8〕李正中.固体理论(第 2版)[M].北京:高等教育出版社,2002.
O 469
A
1673-260X(2010)12-0143-02

