城市房地产项目造价的预测模型

朱晓伟，李文驹

（浙江大学，杭州 310012）

1 基于层次分析法的估价模型

层次分析法[2](Analytic Hierarchy Process简称 AHP)是美国运筹学家T.L.Saaty教授于上世纪70年代初期提出的，对定性问题进行定量分析的一种简便、灵活而又实用的多准则决策方法。该方法自1982年被介绍到我国以来，以其定性与定量相结合地处理各种决策因素的特点，以及其系统灵活简洁的优点，迅速地在我国社会经济各个领域内，如能源系统分析、城市规划、经济管理、科研评价等，得到了广泛的重视和应用。

1.1 房地产价格因素层次结构体系的建立

这里,把类似房地产与估价对象的相似度测算这一过程解读为一个多目标多准则的决策评定过程。设在同一地区的相近时间内，与待估房地产C1，类似的房地产Cn，为多个决策方案;以待估房地产和类似房地产市场价格的制约因素，按照因素的相互关联及所属关系构成多准则的价格因素层次结构体系，形成一个多层次的分析结构模型(参见图1)，并最终把交易案例相似度测算转变为方案层(交易案例的因素修正)相对于目标层(房地产价格)的相对重要性权值确定的数学模型。

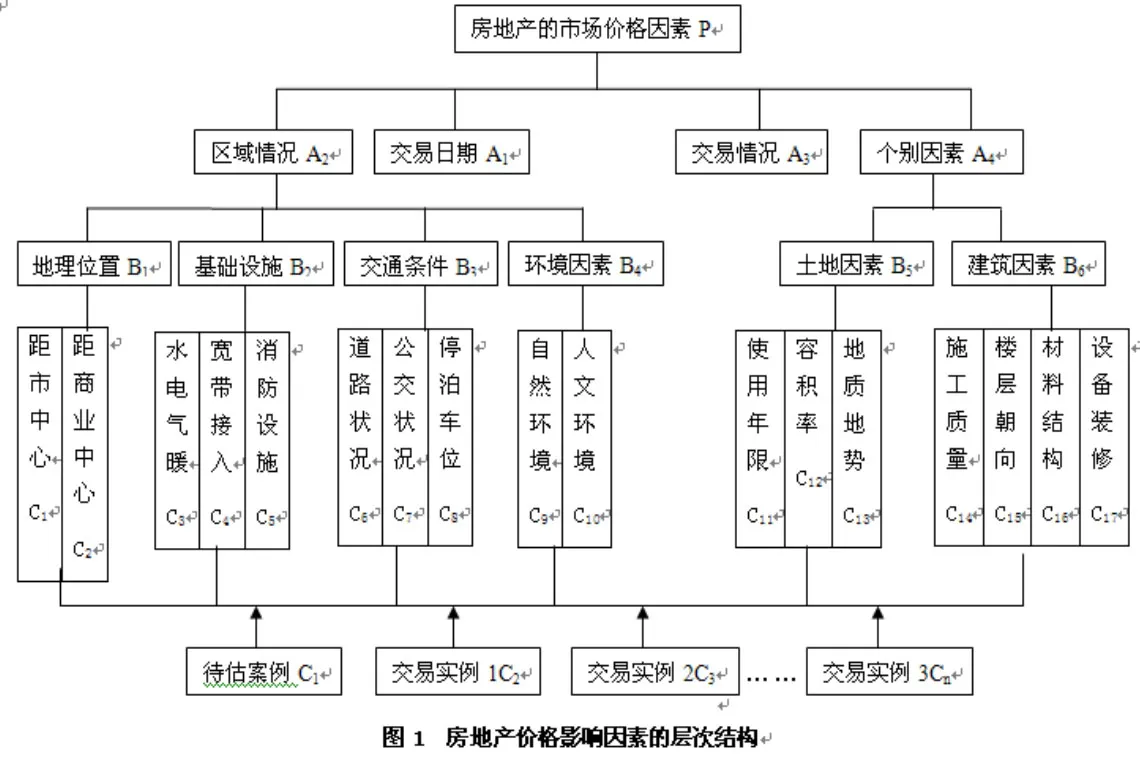
（1)根据影响房地产市场价格的因素间的相互关联及录属关系建立房地产价格因素的层次结构体系(见图1)。

（2)如图1所示，假设C1,C2…Cn为用途相同、建筑结构相同、土地等级相同、交易价格类型相同、价格时点接近的类似房产，C1为待估房产;交易情况一般由主观因素所决定，有明确的定量关系，交易日期与价格也有明确的换算关系，因此交易情况A1,交易日期A3,宜单独修正，修正的计算公式:

类似房地产的比准价格=类似房地产的成交价×100/（100+s）×（100+T）/100

s与T分别为类似房地产的正常交易情况和估价时点的修正系数。

1.2 用1-9标度构造两两比较的判断矩阵

对图1中同一层次的各元素关于上一层中某一准则的重要性，采用1-9标度的专家赋值进行两两比较，构造两两比较的判断矩阵 A=(aij)n×n，其中 aij,元素为 ui与 uj相对某一准则的重要性标度。在这一步中，估价人员要反复回答问题，即针对某一准则，两个因素ui与uj哪一个更重要，重要程度如何?AHP法采用了1-9标度，表1列出了1-9标度的含义。

设w=(wi,w2,...wn)T是n阶判断矩阵A的排序权重向量，当 A为一致性矩阵时，满足AW=λmaxW.λmax是A的最大特征根，W是相应的权向量，经归一化就可近似作为排序权重向量(称为和积法):

表1 1-9比例标度的含义

1.3 计算各层元素对应于系统目标的总排序权重

层次总目标的相对重要性的排序权值计算是从最高层次到最低层次逐层进行的，如果上一层次A包含m个因素A1，A2…Am，其层次排序值分别为 a1，a2…am，下一层次 B 包含n个因素B1，B2…Bn，它们对于因素Aj的层次单排序值分别为 b1j,b2j…bnj(当 Bk与 Aj无联系时，akj=0)，这时 B 层次总排序值为:

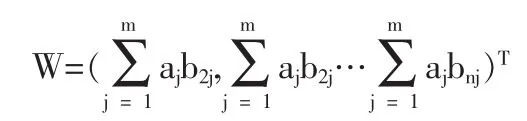
这样，逐层可求出案例层相对与价格的相对重要性排序权值。

2 房地产价格的随机一模糊回归分析

由于房地产市场是一个不确定性很强的市场，房地产实例资料往往来自同时具有模糊性和随机性关系的同一供需圈，它们是典型的随机— 模糊样本，其样本值必同时包含了随机和模糊两类不确定性。所以传统的随机回归方法对分析影响房地产价格的因素已经不再适用了，本文将随机模糊回归分析[3]引入房地产估价中，以便更准确地预测房地产价格。

设随机一模糊变量x1,x2….xm和随机一模糊变量y的每一组样本值，均有线性关系:

其中a0,a1...am为常数，ε是误差变量，设获得了变量为n的样本:

欲求线性回归方程，则取样本yi(xji)对R的隶属函数为:

式中yi(Xji)为样本值；为待回归方程计算所得的y的值，据此，组成目标函数：

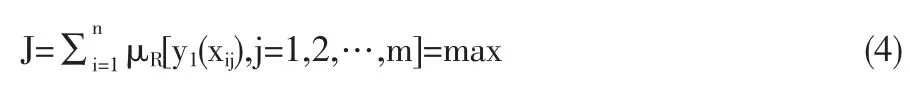
由此可得出求b1,b2,…bm的方程组，则相应的正规方程组有如下的形式:

这里mxixj是变量xi的样本(xi1,xi2,…,xin)和变量 xj的样本(xi1,xi2,…xjn)之间的随机一模糊协方差。mxiyi是变量xi的样本(xi1,xi2,…,xin)与变量y的样本(y1,y2,…,yn)之间的协方差。上述求解随机一模糊回归方程的计算步骤可归纳如下:

（1）选择隶属函数；

（3）由方程组(5)计算 b0,b1,…bm；

（4）根据公式(2)写出线性回归方程。

3 以北京市为例的基于MATLAB的模型求解

根据本文方法，待估房地产为北京市区的一住宅楼，交易时间为2007年，该物业始建于2003年，框架结构，坐北朝南，交通方便，因处于老城区，其绿化条件较差。

第一步：根据估价对象状况和估价目的，从搜集的交易实例中选取符合下列要求的物业:

（1）是估价对象的类似房地产；

（2）成交日期与估价时点相近，不超过1年；

（3）成交价格为正常价格或可修正为正常价格。

这里收集了12个交易案例，由于该地区同类房地产交易频繁，故这12个交易案例均来自该市的同一供需圈内，交易时间均为2007年，房屋建造时间都在2003年以后，均为框架结构。且交易情况、交易日期和个别因素修正量极小。

第二步：按前述方法，对层次总目标的相对重要性的权值进行计算，可得到房地产的价格和量化影响房地产价格的因素及其重要性权值。

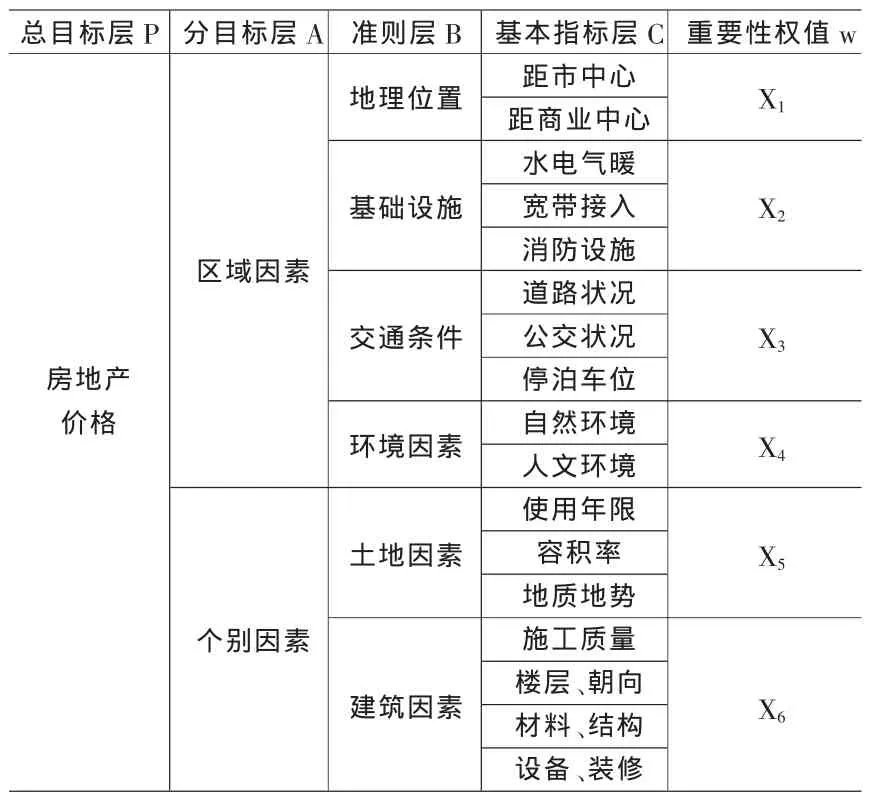
表2 影响房地产价格的因素及其重要性权值

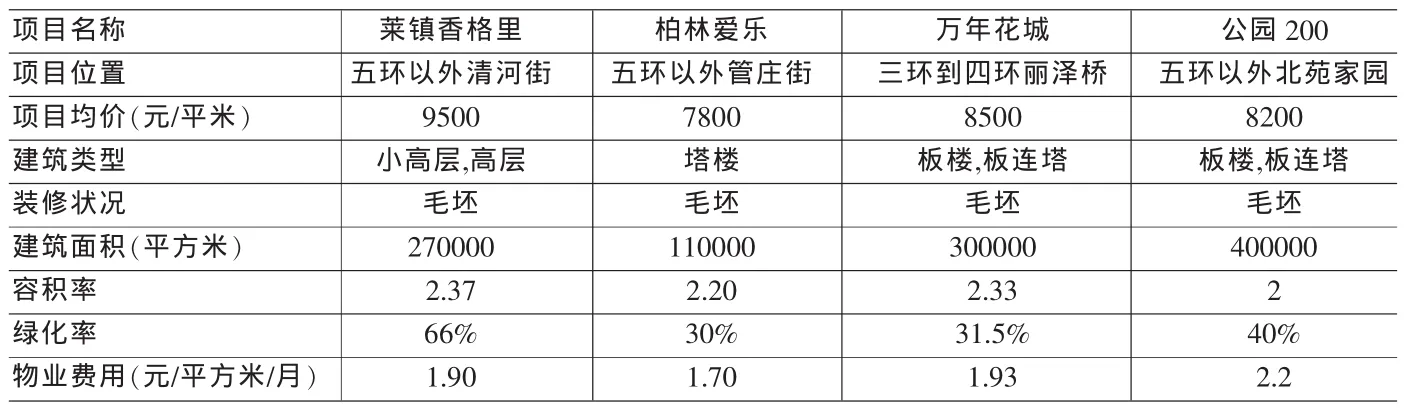
表3

（1）Matlab[6]进行编程，运行程序，输出W，即可得到总排序权重，列入表2。

（2）以北京市莱镇香格里2006下半年销售基价为例。选取与该项目结构、功能近似的柏林爱乐、万年花城、公园200作为可比案例。(符号含义参看图1,w为重要性权值)

P-A层：

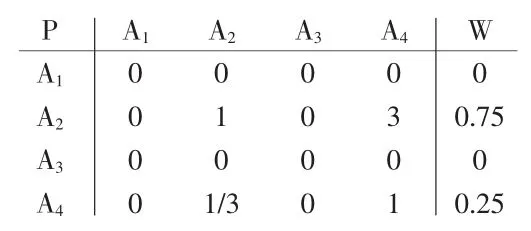
A-B层：

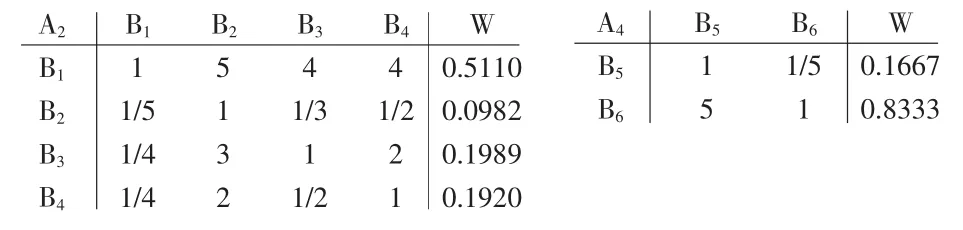
B-C层：

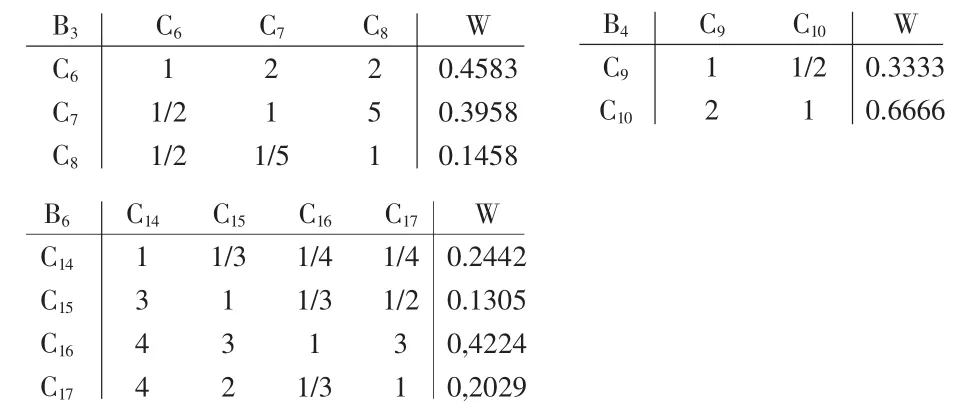
由于类似案例均位于待估项目邻近，故只选有差异的B3,B4,B6等因素比较

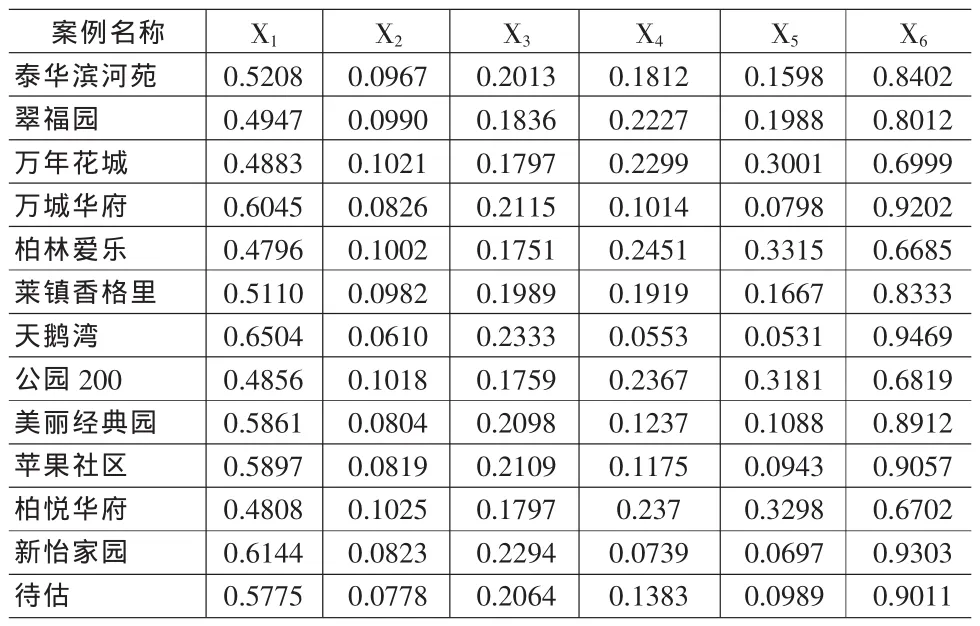
表4

第三步:MatLab编程，对于样本的影响因素和价格进行分析和计算

第四步:求得的线性回归方式为:

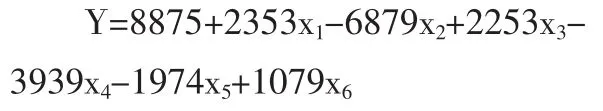
第五步:根据以上公式得出房地产的价格，具体结果列入表5。

表5 房地产价格的评估结果

4 结束语

房地产具有实体性和虚拟性、投资性和消费性、不动性和流动性等相互对立的属性。土地资源实体的有限性和土地虚拟价格无限性的对立，土地资源的稀缺性和垄断性决定了房地产供给的有限性和信息不对称性。利用计算机快速、准确、科学地进行房地产评估是引导房产市场健康发展的重要手段。由表2可知，本文方法所得的评估结果同实际价格相比其误差最大为13%，从12个样本的总体状况来看，符合客观实际，减小了人为因素的影响，这种新型的、基于计算机程序的估价方法相比现有估价方法更能满足现代信息经济社会对房地产估价实时性、准确性、科学性和效率等方面的要求，对遏制房地产泡沫有一定现实意义。但该方法还有许多问题需要进一步的研究，还需做进一步的改进。

[1]冯子平.论房地产价格评估的发展趋势及其标准化体系的建立[J].中国房地产，1995，(4).

[2]赵焕臣，许树柏，和金生.层次分析法[M].北京：科学出版社，1990.

[3]万俊，关柯.模糊数学在城市地价评估中的应用[J].哈尔滨建筑大学学报，1995,28(6).

[4]朱衡君.MATLAB语言及实践教程[M].北京:清华大学出版社、北京交通大学出版社,2005.