应力锥橡胶材料在变温环境下的力学性能

鲁中亚, 马永其,2, 徐 操

(1.上海大学上海市应用数学和力学研究所,上海 200072;2.上海大学理学院,上海 200444;3.上海三原电缆附件有限公司,上海 201206)

应力锥橡胶材料在变温环境下的力学性能

鲁中亚1, 马永其1,2, 徐 操3

(1.上海大学上海市应用数学和力学研究所,上海 200072;2.上海大学理学院,上海 200444;3.上海三原电缆附件有限公司,上海 201206)

利用德国 Zwick020材料试验机,进行高压电缆终端应力锥两种橡胶材料在不同温度环境下单向拉伸大变形力学行为的试验研究,得到不同温度和不同加载速率条件下材料的应力-应变关系曲线,并分析了温度及加载速率变化对材料力学性能的影响.运用Mooney-Rivlin橡胶材料模型,对试验材料进行了理论分析,根据试验结果拟合出相关参数,构建了适用高压电缆终端应力锥两种橡胶材料的本构关系公式.对比不同温度下两种橡胶材料的理论计算和试验的应力值,说明该本构关系满足工程实际需要,为高压电缆应力锥的进一步研究提供了理论基础.

橡胶材料;应力锥;本构关系;拉伸试验

Abstract:Mechanical behavior of large-scale deformation for rubber stress cone of high voltage cable accessorieswas studied with a German Zwick020 material testmachine.Stress-strain relation curveswere obtained under different temperatures and different loading rates. From these curves,influences of temperature and loading rate were analyzed.The material’s mechanical properties were theoretically analyzed with the Mooney-Rivlin model,and some fitting parameters of the material were got from experimental data.Two constitutive equationsof materialwere then constructed,and the stressobtained in the experiment was compared w ith theoretical calculation. It show s that the equations are suitable in engineering practice and can be used for further research.

Key words:rubber;stress cone;constitutive relation;tensile test

近年来,随着我国经济的发展,电力的安全可靠供应越来越重要.北京奥运会举办之前,国家电力监督委员会专门组织开展电力行业安全生产百日督查专项行动,以确保用电安全.现今,我国远距离输电线路都采用高压架空线,而在大城市等人口稠密地区的输电网络和发电厂、大型工厂、交通拥挤的地方大多采用电力电缆[1].电力电缆是用于电力传输和分配的电缆[2].我国电缆制造行业通过引进国外技术、设备和原材料,已有了飞速的发展,但是电缆附件本身结构、制作和连接及运行条件复杂,导致其发展相对滞后.在电力系统故障发生的概率中,电缆附件的故障占到电缆运行故障的 50%以上[3],所以电缆附件的运行安全是关系到整个电网正常运转的重要因素.国内外新建设的高压电缆工程,大多采用预制型电缆终端[4],它是一种较先进的电缆终端,已得到了广泛应用,是目前和将来高压电缆终端技术应用的主流[5].

预制型电缆终端的高效安全运行,需要使橡胶预制应力锥和环氧树脂套管、电缆绝缘之间的界面紧密接触,并保持一定的界面应力.预制型电缆终端的界面应力,主要由弹簧压紧装置的机械力和橡胶应力锥扩张后产生的箍紧力两部分组成.研究表明,当界面压力增大时,界面的电场击穿强度也随之增大,密封度也升高[6],因此,维持满足设计要求的界面应力是预制型电缆终端正常工作的关键所在.在运行过程中,高压电缆终端承受着交变荷载,电缆芯温度最高可以达到 90℃,高电场、高热场都会加速橡胶的老化.此外,绝缘油的渗漏还会引起应力锥材料溶涨,最终都会导致界面应力的变化[7].本研究主要分析橡胶锥的橡胶材料性能与扩张后产生的箍紧力大小的关系,通过试验研究获得高压电缆终端应力锥橡胶材料的应力应变关系,根据试验数据拟合出材料的应变能函数,构建出适用此两种材料本构关系的公式,为进一步研究橡胶应力锥的老化和疲劳导致的可靠性降低奠定基础.

1 试 验

1.1 试验装置

高压电缆终端应力锥橡胶材料单向拉伸试验采用带温箱的德国产 Zwick020材料试验机,最大载荷2 t,电阻加热温箱内的最高温度可达 250℃,加载速率范围为 0.000 5～1 000 mm/min.试验加载过程由微机自动控制,在试验过程中,如载荷为零,试验机会自动终止试验.试验操作过程根据 GB/T 258—1998标准进行,外加载荷和试件变形由试验机自行测量并记录,最后通过应力-伸长率关系曲线表示.试验机温箱的升温速率约为 8℃/min.

1.2 试件

高压电缆终端应力锥橡胶材料包括两种:绝缘橡胶和半导电橡胶.将两种橡胶材料根据GB/T 258—1998标准制成哑铃状试验材料试件,橡胶材料试件厚度为 2 mm.试验段长 25 mm,宽 6 mm.

1.3 试验过程

为提高试验的效率,更好地模拟实际运行工况下橡胶应力锥所处的环境温度,本研究将试验进行如下设计.假设常年室外平均温度为 20℃.在 20,60,70,80,90,120℃均依据 GB/T 258—1998标准,以 500 mm/min的加载速率进行单向拉伸试验.电缆芯在 110,220 kV工况运行时,内部温度分别为 70和 90℃左右,为更好地反映橡胶应力锥的橡胶材料在工作时所处的温度环境对其力学性能的影响,在70,90℃温度下的试验中,除以 500 mm/min的标准加载速率进行加载外,另分别增加 1组以 300 mm/min为加载速率的对比试验.

1.4 试验结果及分析

一般情况下,橡胶材料为不可压缩弹性体[9-10],在单向拉伸状态下,不可压缩橡胶材料的主伸长分别为

式中,λ为试件在拉伸方向的主伸长,L0和 L为试件试验有效段的初始长度和最终长度.橡胶材料的主应力分别为

式中,F为施加的荷载,A0为有效段的初始横截面面积.

试验结果以应力 (MPa)-伸长率 (%)曲线表示,图1、图2分别为绝缘橡胶材料、半导电橡胶材料在500 mm/min加载速率和不同温度下的应力-伸长率曲线.图3、图4分别为绝缘橡胶材料在 70,90℃温度下两种加载速率的应力-伸长曲线.图5、图6分别为半导电橡胶材料在 70,90℃温度下两种加载速率的应力-伸长曲线.

由图1～图6可见,首先,绝缘橡胶材料和半导电橡胶材料力学性能相差很大.绝缘橡胶材料的应力-伸长率曲线变化速率快、应力值大,这说明绝缘橡胶更难以拉伸,更加坚硬.这种性质与绝缘橡胶在外部起绝缘和保护作用是有密切关系的.

其次,两种橡胶材料都对温度比较敏感,其力学性能强烈依赖于温度,但是两种材料的应力-伸长率变化规律又不同.如图1所示,绝缘橡胶材料在相同的伸长率下,在 20℃时应力最小,在 60℃时应力最大,随着温度的升高应力依次减小,但不会小于20℃时的应力.如图2所示 ,半导电橡胶材料在 20℃时应力最大,随着温度的升高应力也依次减小,在 120℃时为最小.这是因为随着温度的升高,导致分子间作用及链段间作用削弱[11],在高温段出现软化,材料刚度降低,在相同伸长率下,应力减小.最后,在相同的温度下,材料刚度随着加载速率的增大而增大.这是因为橡胶材料的高分子链结构的充分伸展需要一定时间,随加载速率的减小,橡胶的高分子链结构能够得以充分伸展[11].在应力缓慢增加的条件下,伸长率得以快速增加,在相同的伸长率下应力减小.

图1 绝缘橡胶材料在 500 mm/m in加载速率下应力-伸长率曲线Fig.1 Stress-strain relation curves of insulating rubber under 500 mm/m in

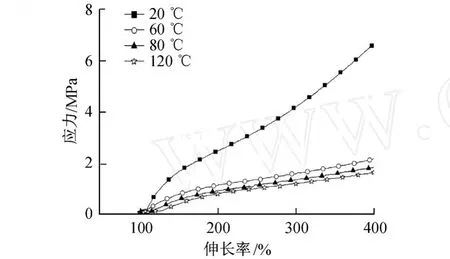
图2 半导电橡胶材料在 500 mm/m in加载速率下应力-伸长率曲线Fig.2 Stress-strain relation curves of sem i-electr ic rubber under 500 mm/m in

图3 绝缘橡胶材料在 70℃、不同加载速率下应力-伸长率曲线Fig.3 Stress-strain relation curves of insulating rubber under d ifferent load ing ratesat 70℃

图4 绝缘橡胶材料在 90℃、不同加载速率下应力-伸长率曲线Fig.4 Stress-stra in relation curves of insulating rubber under d ifferent load ing ratesat 90℃

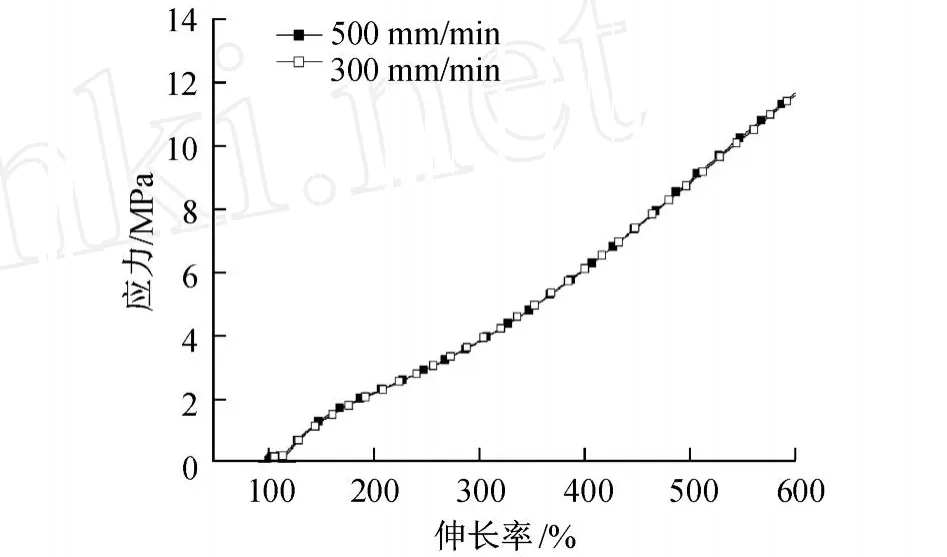
图5 半导电橡胶材料在 70℃、不同加载速率下应力-伸长率曲线Fig.5 Stress-stra in relation curves of sem i-electr ic rubber under d ifferent load ing ratesat 70℃

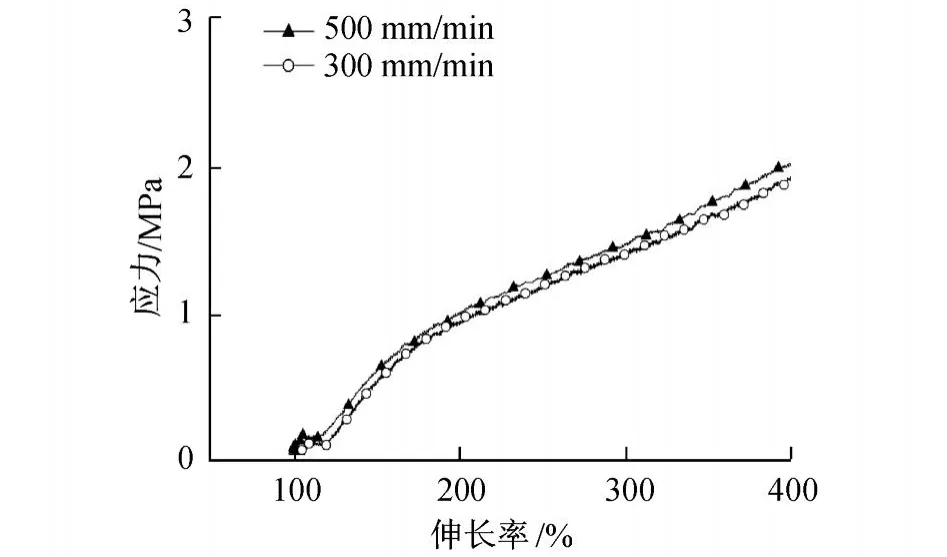
图6 半导电橡胶材料在 90℃、不同加载速率下应力-伸长率曲线Fig.6 Stress-stra in relation curves of sem i-electr ic rubber under d ifferent load ing ratesat 90℃

2 不可压缩超热弹性体本构关系理论分析

按照Mooney-Rivlin方程[12],不可压超弹性材料应力-应变关系可以表示为

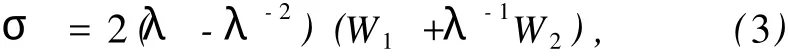
式中,W=W(I1,I2)为材料的应变能函数,I1,I2分别为材料变形张量的第一和第二不变量,W1,W2表示应变能函数对第一和第二不变量的偏导数.Gregory[13]注意到在单轴拉伸应力应变数据之间存在一个简单的比例关系,但必须满足下列两个条件:① ∂W/∂I1≫ ∂W/∂I2;② ∂W/∂I2与 I2无关.

根据最小二乘法,对 60℃下标准加载速率获得的应力-伸长率曲线进行拟合,可以得到该温度下的C1,C2.C1在温度不变时为常数,C2随着应变的变化而变化[14],如表 1所示.

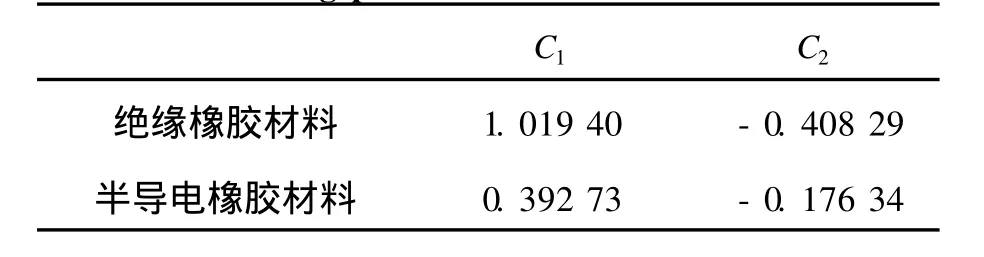
表 1 60℃时两种橡胶材料相关参数Table 1 Fitting parameter s of two rubber sat 60℃

对不可压热超弹性材料,应变能函数的一般形式可以表示为[15]

式中,W(I1,I2)为通常等温情况下的应变能函数,W=W(T)描述温度的影响,一般情况下可以写为[16]

式中,T=T(R)为材料的温度场,C3=Ce,C4=-αμ,Ce为材料的比热容常数,α为材料的体积热膨胀系数,μ为材料的第二拉梅常数,T0=300 K为参考温度[17].由于没有做绝缘橡胶和半导电橡胶相关物理性质参数的试验,W(T)中的参数近似采用天然橡胶材料的相应常数[18],α=6.7×10-4K-1,μ=1.94 MPa,Ce=1 506 J·kg-1·K-1,材料实际密度ρ=870 kg·m-3,则最终相应的应力分量可以表示为

σ =2(λ -λ-2)[C1+λ-1C2+C4(T-T0)].(7)

由式 (7)得到理论计算值,与试验结果的对比如图7和图8所示.

图7 绝缘材料试验结果与理论计算的应力值对比Fig.7 D ifferent between stress of exper iment and theoretical calculation of insulating rubber

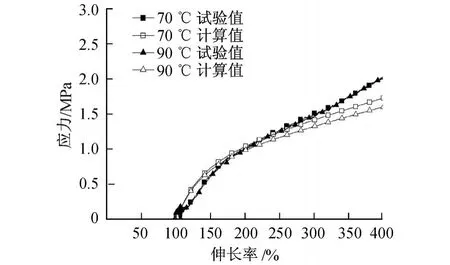
图8 半导电橡胶材料试验结果与理论计算的应力值对比Fig.8 D ifferen t between stress of exper im en t and theoretical calculation of sem i-electr ic rubber

图7为绝缘橡胶材料分别在模拟实际工况下,应力-伸长率曲线的试验值和理论计算值的比较.可以看出:在伸长率小于 200%时,理论计算值和试验值可以很好地吻合;随着伸长率增大,材料在大变形条件下,本构关系变化剧烈,理论计算数据和试验值有一定的差距,这是由于采用相对简单的 Mooney-Rivlin模型和直接采用天然橡胶的材料参数的原因.相关研究表明,Mooney-Rivlin模型可以较好地拟合不可压缩橡胶材料中等应变范围的应变能,不适用于压缩及大应变时硬化的材料[19].但是,由于Mooney-Rivlin模型形式简单,计算量小,同时高压电缆终端应力锥在扩张时橡胶材料受拉伸幅度很小,因此,在伸长率小于 200%的范围内,该本构关系公式很好地满足了要求,可以运用到实际工程中.图8为半导电橡胶材料的理论计算值和试验值的应力-拉伸率的曲线图,吻合情况与图7类似.

3 结 论

(1)高压电缆终端应力锥橡胶材料对温度的变化非常敏感.随着温度的升高,两种材料出现了明显的力学性能改变,其中绝缘橡胶材料在 60℃时刚度最高,20℃时最小,且随着温度的继续升高逐渐下降,因此,绝缘橡胶材料的刚度有一个先上升后下降的过程.但是,半导电材料不同,在相同的伸长率下,应力在 20℃时最大,且随着温度的升高依次下降.

(2)高压电缆终端应力锥橡胶材料对加载速率非常敏感,加载速率越大,材料的刚度越大.试验所用两种橡胶材料均有上述特征.但是,随着温度的升高,受加载速率的影响降低,这说明温度是影响橡胶材料性能的首要因素.

(3)本研究拟合的两种高压电缆终端应力锥橡胶材料的本构方程,在伸长率小于 200%的应变范围内,与试验数据可以较好地吻合.说明在此范围可以实际反映两种材料的本构关系,完全适用于工程实际.

(4)高压电缆终端应力锥橡胶材料性能不稳定,还需要进一步研究其他影响因素,如老化、疲劳等.

[1] 应启良,魏东,高小庆,等.我国高压及超高压交联聚乙烯绝缘电力电缆的应用和发展[J].电线电缆,2001(3):3-9.

[2] 于景丰,赵锋.电力电缆实用技术[M].北京:中国水利水电出版社,2003.

[3] 罗俊华,邱毓昌,杨黎明.10 kV及以上电力电缆运行故障统计分析[J].高压电工程,2003,25(6):14-16.

[4] 王佩龙,车年坚.高压交联电力电缆附件选型的若干问题[J].电力设备,2004,5(8):18-22.

[5] 李新平,刘守功,曹晓珑,等.高压电缆终端结构设计的进展[J].电线电缆,2002(3):11-14.

[6] 李仁飞.两种电缆附件的技术和安全性比较[J].山东电力技术,2004,137(6):78-79.

[7] 韩轩,马永其.高压交联电缆终端预制橡胶应力锥的研究进展[J].绝缘材料,2007,40(4):12-17.

[8] 全国橡胶与橡胶制品标准化技术委员会橡胶通用物理试验方法分技术委员会.GB/T 258—1998硫化橡胶或热塑性橡胶拉伸应力应变性能的测定[S].北京:中国标准出版社,1998.

[9] MOONEY R.A theory of large elastic deformation[J].J Appl Phys,1940,11:582-592.

[10] RIVLIN R S. Large elastic deformation of isotropic materials[J].Philos Trans Roy Lond Ser A,1948,240:459-508.

[11] 刘微,金日光,励杭泉.高分子材料时-温等效性的研究[J].北京化工学院学报,1991,18(1):24-26.

[12] RIVLIN R S.The elasticity of rubber[J].Rubber Chem Technol,1992,65(3):51-67.

[13] GREGORY M J. The stress-strain behavior of filled rubbers at moderate strains[J].Plastics and Rubbers Materials and Applications,1979,4(4):84-88.

[14] WARD IM.固体高聚物力学性能 [M].徐懋,译.北京:科学出版社,1988:55-100.

[15] N ICHOLSON DW,NELSON N.Finite element analysisof hyperelastic components[J].Appl Mech Rev,1998,51:303-320.

[16] 黄筑平.连续介质力学基础 [M].北京:高等教育出版社,2003.

[17] 爱林根 A C.连续统力学 [M].程昌钧,俞焕然,译.北京:科学出版社,1991.

[18] 刘登祥.橡胶及橡胶制品 [M].北京:化学工业出版社,2005.

[19] 朱艳峰.橡胶材料的本构模型[J].橡胶工业,2006,53(2):119-124.

(编辑:孟庆勋)

Rubber M echan ical Proper ty of Stress Cone in Var iable Tem perature Fields

LU Zhong-ya1, MA Yong-qi1,2, XU Cao3
(1.Shanghai Institute of Applied Mathematics and Mechanics,ShanghaiUniversity,Shanghai200072,China;2.College of Sciences,Shanghai University,Shanghai200444,China;3.Shanghai Sanyuan Cable Accessories Co.,Ltd.,Shanghai201206,China)

TM 212;TN 304

A

1007-2861(2010)03-0237-05

10.3969/j.issn.1007-2861.2010.03.004

2009-02-18

马永其 (1966～),男,副教授,博士,研究方向为柔性输电技术及其稳定性.E-mail:yqma@mail.shu.edu.cn