用马尔可夫链的蒙特卡洛方法更新及预测连续油藏模拟模型
编译:杨菁华 王奇 (西安石油大学石油工程学院)
审校:王青青 (西安石油大学石油工程学院)
用马尔可夫链的蒙特卡洛方法更新及预测连续油藏模拟模型
编译:杨菁华 王奇 (西安石油大学石油工程学院)
审校:王青青 (西安石油大学石油工程学院)
大多数油藏模拟研究都局限于静态范畴,因时间和预算限制,未知参数明显减少,这容易导致低估预测的不确定性或作出不明智的决策。马尔可夫链的蒙特卡洛(MCMC)方法已被用于静态研究以对预测参数空间的不确定性进行严格的量化考察。但这些方法在长期性和系列稳定性方面存在局限。文中将MCMC应用于实时油藏建模。较之传统方法,MCMC方法在某一特殊时间点上应用更少的模型来实现合理的概率预测,它也提供了一种随时校准不确定性预测的机制。
连续油藏模拟 马尔可夫链蒙特卡洛 概率预测 不确定性量化
1 背景
1.1 不确定性量化技术
对产量预测中的不确定性进行量化完全依赖于历史拟合。进行历史拟合包含三个主要步骤:第一,根据描述油藏几何与流动特性的整套参数来定义油藏;第二,根据预估的概率分布对油藏未知参数进行赋值;第三,从预先的分配油藏模型可作为实际模拟例子,并在目标函数中量化模拟结果和观察数据的差异。许多方法用于寻求合理的模型,某些历史拟合的技术——梯度法技术,它们的目标就是最优化,即模拟结果最符合观测结果的模型就是所需要的模型。用梯度法进行的不确定性量化也许还不是最完美的方法,因为它只在目标函数的一个或多个极疏区的相邻区取样。MCMC方法已广泛应用于从一个复杂的分布函数中取样,特别是当不知道函数的精确形式的时候。
在油藏模型研究中,MCMC技术用于研究贝叶斯推断的后验分布。最后分布只不过产生于一套案例中油藏模型所用的样本。首先,一个随机模型取样于一个先验分布的样本,这是马尔可夫链的出发点。其次,第二个模型被随机选择但受限且关联于马尔可夫链中已存在的前一个模型。当这个马尔可夫链足够长后,可以用此链中的模型产生后验分布。生成未知分布的另一种相关方法叫作遗传算法(GAs),它有多个相关的应用软件。遗传算法是基于控制自然界遗传基因规则、类别涉及面广的一类最优化算法。
在遗传算法中的一个称为“繁殖”的过程中,特种油藏模型的子模型产生于先前运行的模型混合参数值。最后应用所有的子模型生成一种分布。较之GAs,MCMC方法在统计上更严格。MCMC也被当作是遗传算法的一个类型,因为下一个模型依赖于其前一个模型,这在GAs就是其母模型。
1.2 实时数据与综合最小方差线性递推估算滤波器
综合最小方差线性递推估算滤波器 (卡尔曼滤波器)技术广泛应用于天气预报,近来应用于石油工程以进行概率预测。卡尔曼滤波器是一种蒙特卡洛手段,是一种通过连续模型校正而进行不确定性量化的技术。较之传统的历史拟合中进行同步数据同化,EnKF(综合卡尔曼滤波器)要顺序进行。EnKF从受静态数据 (如岩心、测井及构造资料)约束的整体油藏模型开始运行。当数据可用时, EnKF用来自于综合模型的静态信息和模型预测数据更新每个模型的实现。因此,EnKF生成一套受生产历史约束的拟模型实现,而且从理论上讲,它应该尊重先前的静态或地质信息。然而,由于受依赖于样本数量或模型实现的所有统计测量中固有的杂波影响,对于小的整体规模,EnKF更新能导致地质不协调实现。因此,如果最终的模型实现尊重历史生产数据,那么模型可能就不符合先前的地质信息。在EnKF过程中使用大的整体规模可以减少运行的困难,但对于油田规模计算费用可能比较昂贵。EnKF仍是为达到历史拟合而进行积极研究的主题,并且该技术正致力于解决运行中的难题。
2 连续模拟过程
用连续MCMC方法进行历史拟合以及生成概率预测需要几个部分相结合:首先,不确定性油藏的参数以及先验分布必须是确定的。其次,既然将来的油藏动态的不确定性通常要通过一套油藏模型的模拟动态来评估,那么必须有在参数空间取样以及生成油藏模型的方法。MCMC方法在这里被用来探究不确定性参数空间,并自动生成运行模拟的编码。针对每一示例模型,随着历史拟合的进行,预测也一并进行,同时运行结果也被存储起来。在连续的历史拟合过程中,油田现场的新数据也一直被加入目标函数中。被更新的目标函数致力于后来的模拟运行。最后,各个运行结果被合并入概率预测。
2.1 参数化
在作任何模拟之前都必须首先决定考虑哪些不确定性参数。一旦确定了相关的参数,就要指定先验分布 (这里通常是连续的)以在数量上描述参数的不确定性。正确的分布类型通常是建立在油藏特征数据上的。后期的分布就在贝叶斯框架内定义,而先前的分布根据观测的动态数据作出修正,表示如下:
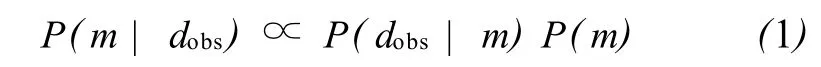
式中dobs——从油田现场上观测的动态数据,如含水率;
m——不确定性参数;
P(m)——不确定性参数的先验概率分布;
P(dobs|m)——与观测数据有关的似然函数;
P(m|dobs)——后期的分布函数。
如果假设先验模型和数据误差服从正态分布,那么这里的后验分布P(m|dobs)就成为如下形式(Howard,2005):
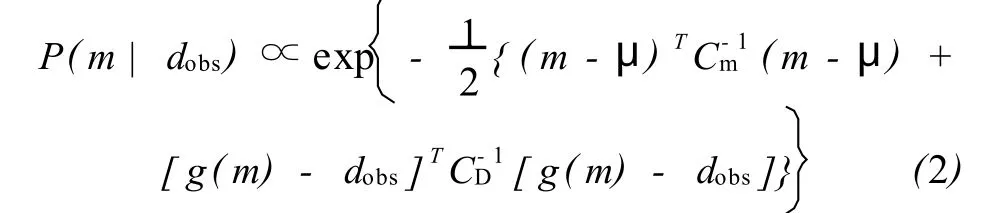
式中g(m)——符合不确定性参数的先验概率分布m的模拟油藏响应 (曲线);
Cm——参数协方差;CD——资料协方差。
2.2 目标函数
目标函数是从数量上评估一个独立模型再现油田现场观测数据的满意程度的函数。这一项被定义为如下后验分布函数的一部分:
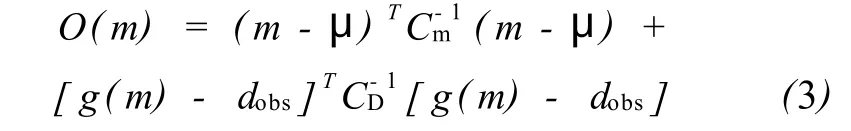
在 (3)式中,(m-μ)T(m-μ)是先验项;[g(m)-dobs]TC-1D[g(m)-dobs]是似然项;μ表示先验平均值。目标函数的结果就是先验信息与观测信息的结合,是一个在贝叶斯框架内后验分布结构的推论。
2.3 Metropolis-Hasting MCMC算法
该MCMC方法的主要目标是构造一个平稳分布与后验分布相匹配的马尔科夫链。这种后验分布典型地定义在多维参数空间上并常有多路系统式。这里所使用的 Metropolis-Hasting MCMC方法(Hastings,1970)常被用来从复杂后验分布中采样,其随机步进M-H采样过程如下:
(1)从先验分布中随机采样一套参数,表示为;
(2)从状态ti时刻到ti+1,mti+1=mti+σ ε,其中,ε是一个标准的正态随机变量;σ是一个比例因子;
(4)从0~1间的均匀分布中随机取一个数y。如果y≤R,则接受链中的mti+1;否则又将mti放入链中;
(5)回到第 (2)步。
2.4 连续数据的同化作用
在连续模拟过程中的不同时间点上,油田现场新数据就显得很有用了。由于通常会设想油田现场的信息越丰富则导致预测和不确定性评估的效果就越好,因此尽快在模拟过程中引入新数据是有利的。当更多的数据加入,则 (3)式中将包括更多的观测及模拟数据点。这样,观测数据的限定不符合目标函数中相关项的状况就将随着时间的推移而改变。尽管持续变化的目标函数在统计上是不严格的,但可以假设在这种违规情况下能产生合理的概率预测。
2.5 概率预测
模拟过程的最后一步是将为单独的马尔可夫链样本所做的生产预测合并入概率预测中。在连续的MCMC过程中,通过使用足够多的最新采样模型可在任何时候生成概率预测。要么用少量的模型以使改变目标函数的影响最小,要么用大量的模型以使获取可代表后验分布的平稳系列分布的机会最大,这二者之间需要寻求一个可以接受的平衡。
3 PUNQ-S3油藏实例研究
PUNQ-S3人造油藏作为在生产预测中量化不确定性的测试实例已应用了很多次。PUNQ-S3油藏模型是一个基于实际油田的5层3相人造油藏(Bos,1999)。该模型包括13 300(19×28×25)个网格块,其中1761个网格块起作用。油藏被东部和南部的断层所限制并与西和北边相当厚的含水层有关系。带井位的结构如图1所示,图中有一个小气顶在中央并以红色显示,6口生产井表示为黑色的圆点。石油行业和学术理论上的几个合作伙伴用不同的方法来检验历史拟合与不确定性量化技术。这个 PUNQ项目的目标就是确立一种方法——可以通过适当方式将油藏模型、油藏参数、油井观察结果的不确定性与生产预测的不确定性结合起来。
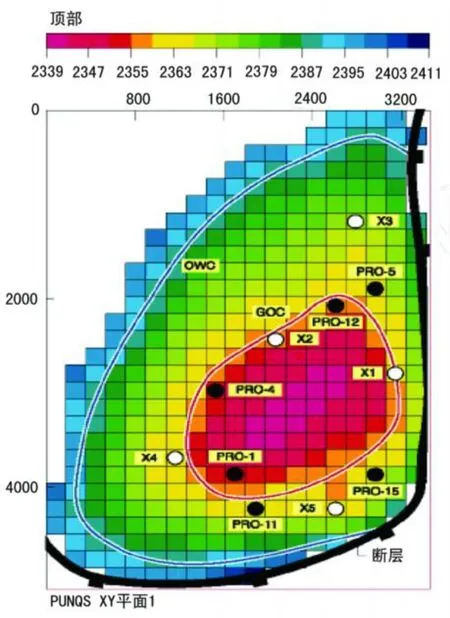
图1 PUNQ人造油藏结构图
用来确定不确定性参数及指定先验分布的过程与传统上模拟研究中评估输入不确定性时所做的工作是一致的。在PUNQ-S3模型中,假设孔隙度呈正态分布,而渗透率呈对数正态分布。另外,研究中的不确定性参数不直接使用孔隙度和渗透率值而是孔隙度和渗透率的乘积,在运行模拟过程中,这些乘子应用于孔隙度和渗透率底图。这样做的效果与直接使用孔隙度和渗透率值的效果相同,但是这种方法简化了实施过程。对每一层使用统一的属性值绘制底图。基于Barker 2001年提供的平均孔隙度常量值,垂向和纵向渗透率通过 (4)、 (5)式(Gu and Oliver,2004)计算得到。表1列出了底图中使用的平均孔隙度和渗透率值。
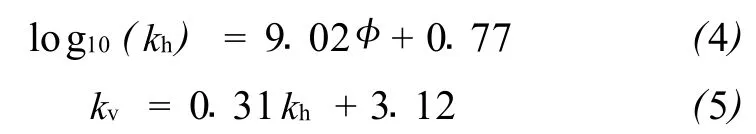
式中,kv表示垂向渗透率;kh表示横向渗透率。
用每层6个同源区对PUNQ-S3模型进行参数化。另外,通过分裂油藏的方式将各区视为相互独立的区域,这一点是基于实时地质描述的,指示油藏广泛分布着东南走向的优质夹层 (Imperial College,2007)。这样,在先验分布中,5层6区3个属性 (孔隙度、垂向渗透率和横向渗透率)就产生总共90个未确定的乘子。孔隙度乘子被指定服从中值为1、标准偏差为0.3的正态分布 (Barker et al,2001)。基于 (4)、(5)式,垂向和横向渗透率乘子被指定服从中值为1、标准偏差为1.35的对数正态分布。为防止出现极端和不实际的渗透率值,此乘子分布被冠以上不过4而下不过0的限制。同样,孔隙度范围在0~2.28。

表1 PUNQ-S3油藏每层的平均孔隙度、渗透率值
3.1 目标函数
由于在研究中确定的不确定性参数是孔隙度和渗透率,目标函数变为:
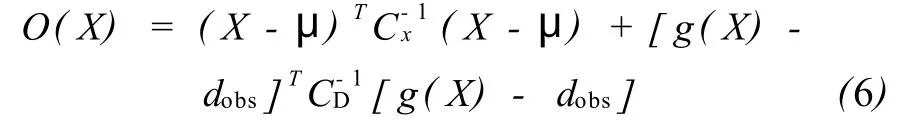
式中,X代表不确定的乘子。
在实验过程中,在第5、6、7、8、9年初顺序加入历史资料。因此,当加入新数据时,目标函数中的观测资料值的数量成倍数增加。
3.2 参数空间研究
在连续历史模拟过程中,模拟运行过程是与历时8.04年的观测资料进行拟合。进行的预测是16.5年的生产经历。PUNQ-S3模型连续模拟开始于第4.5年,持续到第9年底,并作出16.5年的预测。在第一个半年 (从第4.5年到第5年),用MCMC采样方法的模拟中有4 500个模型作为样品,并且在其余的年份里每年样本模型数为9 000,最后模拟样品总数是49 500。所有这些都假设9 000个模型的运行都发生在一年中的实际时间,即每小时运行一个模型,这不是今天石油行业中用于油田模拟的非典型的运行频率。图2显示模拟运行的累积次数与油藏生产时期的对比。包括在目标函数计算中的额外数据也导致目标函数更大且引起目标函数曲线中太多的数值起落跳跃 (图3)。
3.3 预测
一个独立的预测是与每一次历史拟合一起运行。在第5、6、7、8、9年和第10年,利用在链中可用的样品模型在相应的时间进行概率预测。通过过去一年 (或第5年中的半年)的模拟运行可以生成这些概率预测,这些概率预测的累积分布一起显示在图4中。
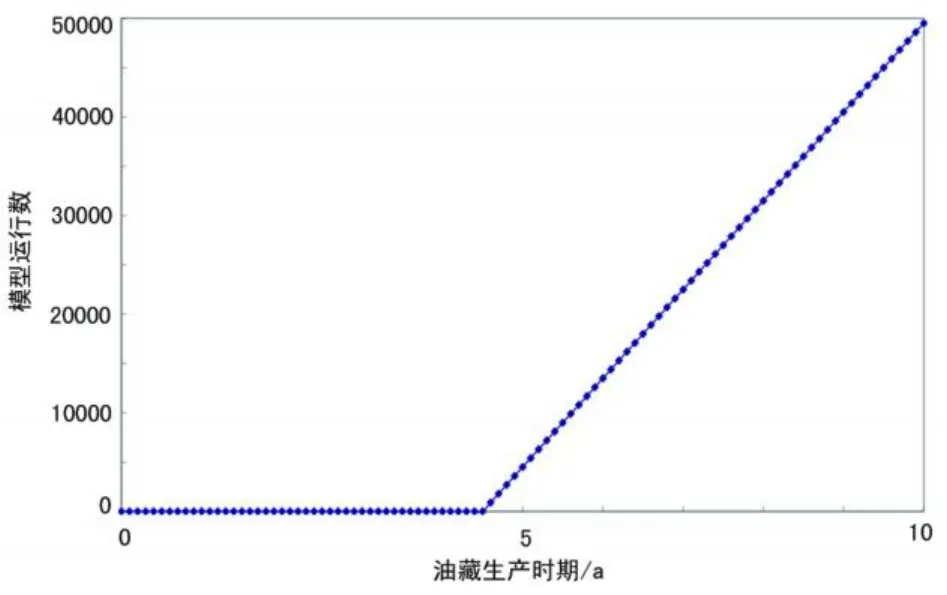
图2 连续测试中模型运行数与油藏生产各时期的关系曲线
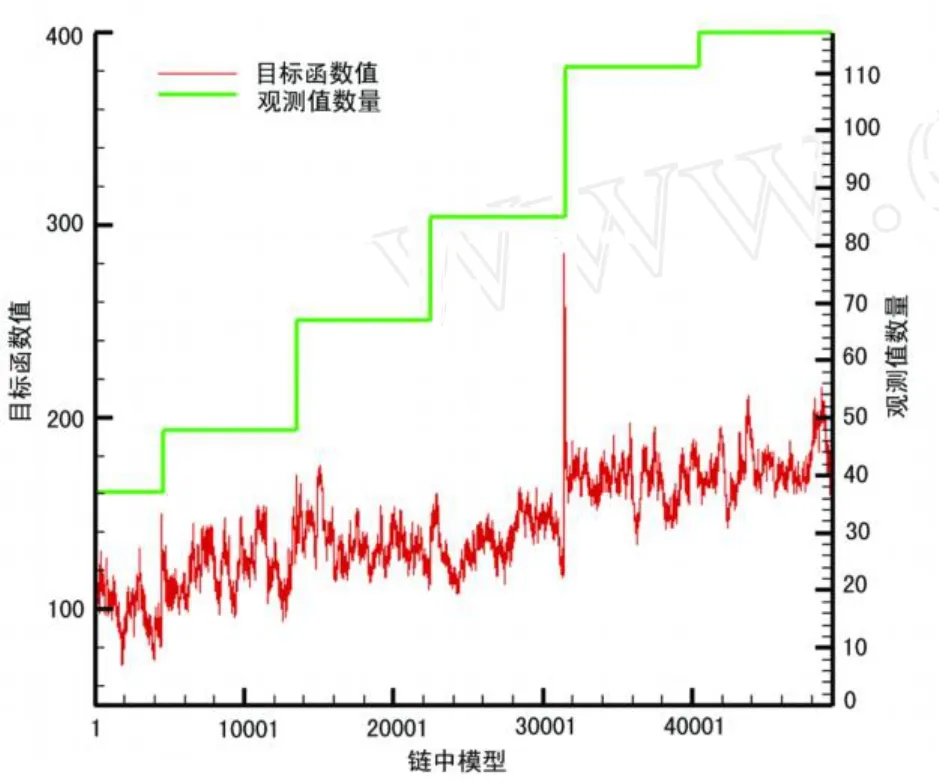
图3 目标函数与连续实例中MCMC链模型的对应关系
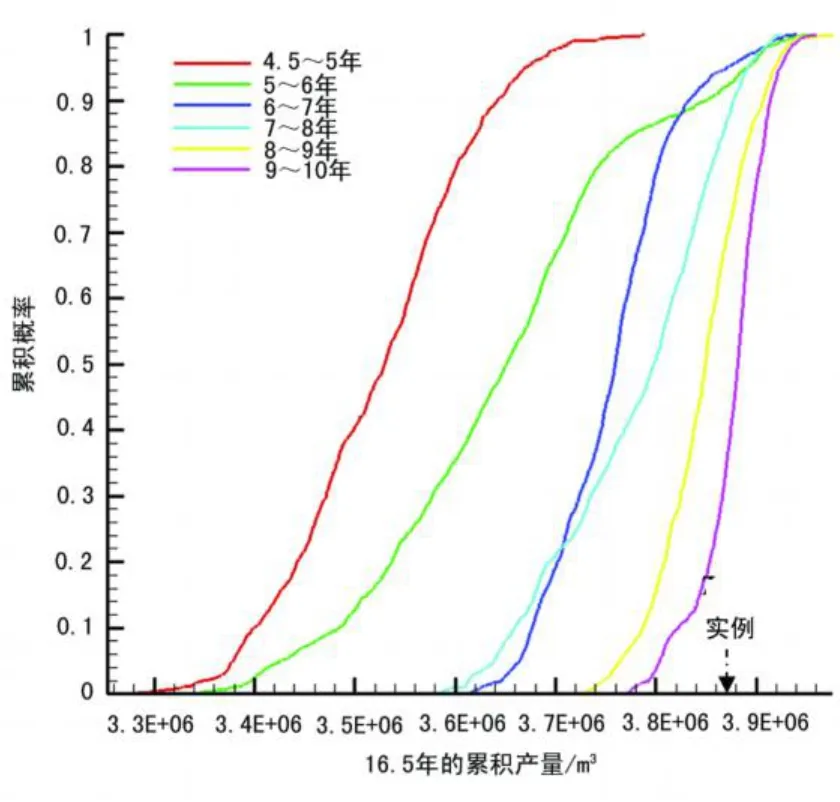
图4 累积分布函数的比较
3.4 不确定性估计的校准
从图5中可以看出,前3个预测没能反映真实情形,在4.5~5年间偏离明显。因此,在前几年里不确定性明显淡化了,这可能归因于先验分布中对不确定性的低估,或是对观测资料误差的低估。即使没有大量的可用动态资料,人们也总是要去量化不确定性。为了增加不确定性,可以在先验分布或观测资料或两者中使用更大的标准差。为了克服这些缺点,增大了先验乘子的标准差。渗透率乘子标准差从1.35增大到20,而孔隙度乘子标准差从0.3增大到0.5。伴随着标准差的增大,先前的后验分布被重新建立,直到它们在本质上支持所有继发的后验分布。
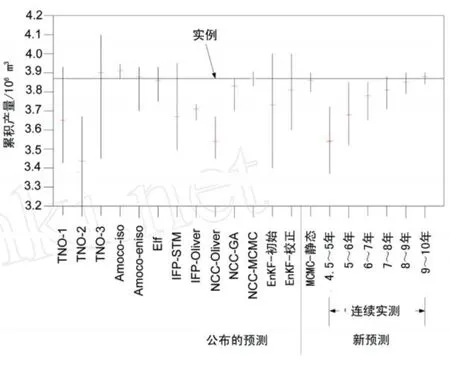
图5 连续实例预测与PUNG油藏分布的预测值的对比
4 结论
MCMC方法是一种应用于历史拟合与不确定性量化的强有力工具。通过对油藏的历史拟合及其整个生命周期的连续预测,随着时间的推移和观测资料的增加,预测不确定性范围逐渐变小。较之MCMC方法传统上应用于过去一时间上的模拟研究,连续MCMC方法可用很少的模型在特别的时间点上进行合理的概率预测,这是因为连续方法得益于最新观测资料同化前的模型运行。在油藏的长期生产中持续建模可考虑以下方面:在参数化过程中获得更多的不确定性参数,更多的样本以及由此造成的参数空间大得多的片断取样。这应该最终导致更可靠的概率预测。
连续的模拟方法也提供一种从始至终的不确定性估计校准机制。如果观测到后验分布除了变窄以外始终发生的跳跃起伏,那么可以放大先验分布中的标准差或者增加观测资料以增加不确定性。应该采取调整措施直到继发的后验分布与所有先前的分布相一致。
资料来源于美国《SPE 119197》
10.3969/j.issn.1002-641X.2010.6.003
2009-03-23)

