镀膜眼镜镜片减反射膜层的选择

许亚娟 王本平 刘红军/文

镀膜眼镜镜片减反射膜层的选择

许亚娟 王本平 刘红军/文

本文以光波的电磁理论为基础，从多光束干涉的原理出发，理论推导出镀膜眼镜镜片减反射膜层的光强反射率与入射光的波长、膜层厚度、膜层的折射率、镜片基体折射率的关系，为镜片镀膜工艺提供合理的科学依据。

减反射膜；反射率；薄膜干涉

光照射到镜片表面时发生反射，光能损失，透过镜片的光线变少，影响人眼的视物。此外，光在镜片的反射容易造成杂散光、偏光等光学污染，这不仅有损自身的美观，还影响行人的视觉，严重时可酿成道路交通事故。为减少反射光的损失，很多眼镜企业选择在镜片表面镀上一层透明的介质薄膜，使入射光在薄膜上下表面的反射光干涉相消，反射光能减少，透射光能相对增大，这样的薄膜叫做减反射膜。

1 镀膜前的反射率

假设光由折射率为n1的介质垂直入射到折射率的介质表面上时，由菲涅尔反射公式可知，不论是平行分量还是垂直分量的反射光光强反射率[1]

当光从空气垂直入射到镜片基体n3=1.5，代入(1)式得R=4%。

2 镀膜后的反射率

假设光垂直入射到透明的介质薄膜，反射光的讨论一般应用多光束干涉的原理[2]。如图1所示，入射光在介质薄膜上表面（界面Ⅰ）发生反射和折射，透射光在减反射膜的→下表面（界面Ⅱ）发生反射和透射，反射光重新回到界面Ⅰ发生反射和折射。图中n1为空气折射率，为n2薄膜折射率，n3为镜片基体折射率，d为薄膜厚度。

图1 薄膜干涉

3 讨论和总结

人眼视觉最敏感的波长λ0=550nm的绿光至黄绿光，为使黄光的反射率降至最低，取λ0=550nm，可见光两侧的紫光和红光光强反射率无法降至最低。

3.1 减反射膜层光强反射率R与λ的关系

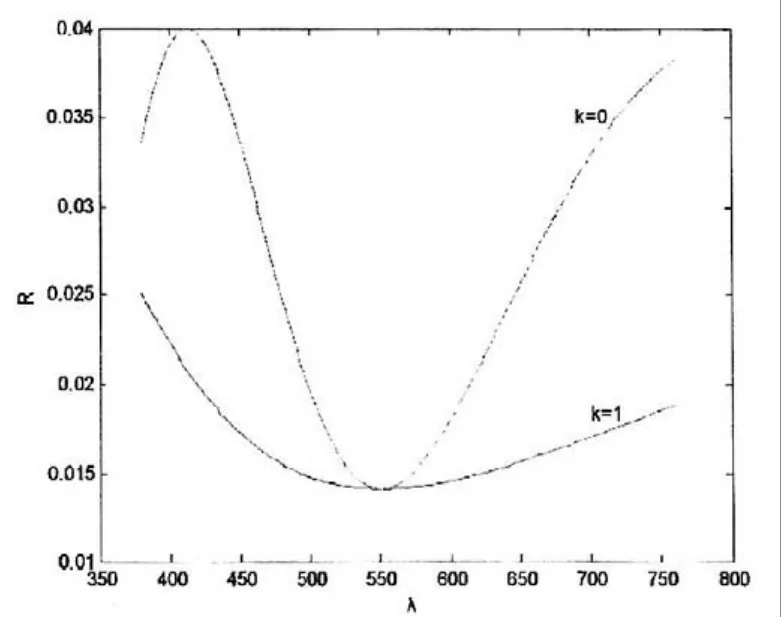
图2 光强反射率R与入射光波长λ的关系

在正入射条件下，n1=1.0，n2=1.38，n3=1.5，λ0=550，k=0或k=1时，减反射膜层的光强反射率R与入射光λ关系如图2所示。从图2可以看出，k=0和k=1时，在λ=λ0=550时，光强反射率都降至最低，可见光两侧的紫光和红光光强反射率均有所提高，但都不大于不镀膜时的反射率R=4%，还可以看出k=1时的紫光和红光光强反射率比k=0时的紫光和红光光强反射率高，当光谱两侧光的光强反射率与光谱中间光的光强反射率差别增大时，镜片表面容易产生眩光[4]，影响行人的视觉，严重时可造成交通事故，因此，取k=0时即膜层的厚度最薄时，镜片膜层减反射效果最佳。显然仅镀一层减反射膜不可能对所有波长和所有入射角的光都是减反射的。要满足一定的减反射要求，可以通过镀多层膜来实现更低的反射率。

3.2 减反射膜层光强反射率R与n2的关系

图3 光强反射率R与薄膜折射率n2的关系

在正入射条件下，n1=1.0，n3=1.5，λ0=550，λ=550，k=0时，减反射膜层光强反射率与关系如图3所示。

从图3可以看出，当n2=即1.2247时，光强反射率R达到0，n2越接近1.2247，光强反射率R越小，n2越远离1.2247，光强反射率R越大。此时的目前找不到一种透明介质的折射率正好是1.2247，既稳定又能够牢牢地附在镜片基体上的材料，常用折射率n=1.38的MgF2 镀在玻璃上。

3.3 减反射膜层光强反射率R与n3的关系

图4 光强反射率R与薄膜折射率n3的关系

在正入射条件下，n1=1.0，n2=1.38，λ0=550，λ=550，k=0时，减反射膜的光强反射率与关系如图4所示。从图4可以看出，当n=时，光强反射率31 R达到0，n越接近 ，光强反射率R越小，n越32远离 ，光强反射率越大。当减反射膜的折射率一定时，选择折射率合适的镜片基体材料也相当重要，不能一概而论说基体折射率越大膜层光强反射率就越低。

综合图3、图4所知，当n2∈(n1，n3)时，无论薄膜的厚度如何，透明介质薄膜都起到减反射的作用;当n2＞n3＞n1时，透明介质薄膜起到增反射的目的。增反膜原理可为抗辐射镜片和防紫外镜片的生产制造提供参考。

[1]黄琳．增透膜的选择[J]．浙江工业大学学报，2003，31（6）：666～669

[2]陈丽菊；肖胜利；朱峰等．对光学薄膜反射率的讨论[J]．太原师范学院学报（自然科学版），2005，4（3）：77～81

[3]赵秀琴．增透膜和增反膜[J]．太原师范学院学报（自然科学版），2003，2（4）：42～45

[4]杨建荣；孟建国；何秀仁等，QB2682-2005，镀膜眼镜镜片减反射膜层性能质量要求

作者单位:国家眼镜产品质量监督检验中心