图形的变换

■杨丛海

图形的变换

■杨丛海

复习要求

图形的变换包括平移与旋转，轴对称图形，放大与缩小等知识，在生活中有着广泛的应用。整理复习时要从它们的基本特征入手，比较分析其相同点和不同点：平移和旋转的相同点是不改变图形的大小和形状，不同点是运动方式不同；放大与缩小只是图形的大小改变而形状不变。关于轴对称图形重点理解其基本特征和性质，能根据“对应点到对称轴的距离相等”画出一个图形的对称图形。同时还要学会运用图形变换的一些基本方法设计图案，并学会灵活分析、合理解决一些简单的实际问题。

平移与旋转

一、填空。

（1）物体或图形作平移运动时，是在（ ）方向上移动，而（ ）没有发生方向上的改变。

（2）物体或图形以一个（ ）或一个（ ）为中心进行圆周运动，就是旋转现象。

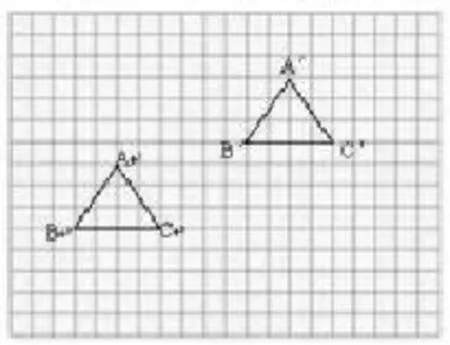
（3）如右图，把三角形从位置甲（△ABC）平移到位置乙（△A＇B＇C＇），三角形先向右平移（ ）格，再向上平移（ ）格；也可以先向上平移（ ）格，再向右平移（ ）格；还可以先连接经过A、A＇两点的一条直线，再沿（ ）把三角形从位置甲平移到位置乙。

（4）大风车在风力的作用下快速地旋转，所看到的图形是一个（ ）。

（5）一个长方形绕一条边旋转一周得到的立体图形是（ ）；一个直角三角形绕一条直角边旋转一周得到的立体图形是（ ）；一个半圆形绕直径旋转一周得到的立体图形是（ ）。

（6）在括号里写出图形的变换过程。

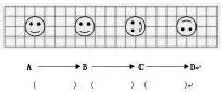
二、判断。（在括号里正确的打“√”，错误的打“×”）

⑴从0时到12时，时针要旋转360°。 （ ）

⑵跳绳时人和绳都在旋转。 （ ）

⑶一个长方形绕其中一条边旋转360°就可以得到一个圆柱体。 （ ）

⑷平移和旋转都不会引起图形形状和大小的改变。 （ ）

⑸正方形或长方形绕着它的中心旋转90°都能够和原图形重合。 （ ）

三、操作。

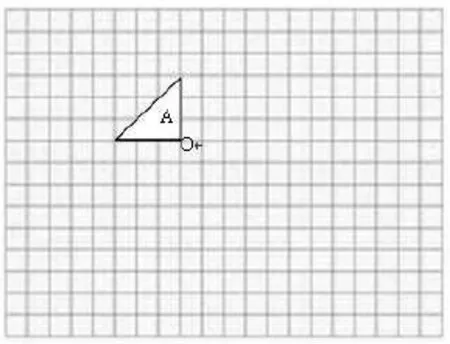
将图A向右平移5格，绕O点顺时针方向旋转90°得到图B，将图B向下平移4格，绕O点顺时针方向旋转90°得到图C，将图C向左移5格，绕O点顺时针方向旋转90°得到图D。

四、设计。

利用下面图形设计一幅美丽的图案。

轴对称图形

一、填空。

⑴如果某一个图形沿一条直线折叠能够互相重合，那么这个图形就是（ ）图形，这条直线就是（ ）。

⑵正方形有（ ）条对称轴，长方形有（ ）条对称轴，等腰三角形有（ ）条对称轴，正三角形有（ ）条对称轴，等腰梯形有（ ）条对称轴。

⑶圆的对称轴有（ ）条，半圆形的对称轴有（ ）条。

⑷在对称图形中，对称轴两侧相对的点到对称轴的距离（ ）。

⑸下面字母中是轴对称图形的有（ ）。

二、判断。（在括号里正确的打“√”，错误的打“×”）

⑴通过一个圆的圆心的直线是这个圆的对称轴。 （ ）

⑵三角形和平行四边形都不是轴对称图形。 （ ）

⑶等腰梯形是对称图形。 （ ）

⑷正方形只有一条对称轴。 （ ）

三、选择。（在括号里填上表示正确答案的序号。）

(1)下列图形中，不是轴对称图形的有（ ）。

A.长方形 B.直角梯形 C.等腰三角形

⑶下列图形中，对称轴最多的是（ ）。

A.等边三角形 B.正方形 C.圆

⑷要使大小两个圆有无数条对称轴，应采用的画法是（ ）。

四、操作。

⑴画出轴对称图形的对称轴。

⑵画出轴对称图形的另一半。

放大与缩小

（此部分内容请参照教科书自拟复习题自主复习）