n阶线性非齐次微分方程初值问题的矩阵解法

曹玉平

(连云港职业技术学院基础部,江苏连云港 222006)

n阶线性非齐次微分方程初值问题的矩阵解法

曹玉平

(连云港职业技术学院基础部,江苏连云港 222006)

借助矩阵指数函数和状态转移矩阵的概念,结合线性代数和微分方程的有关结论,给出了 n阶线性非齐次微分方程初值问题的矩阵解法。

线性非齐次微分方程;初值问题;矩阵解法

常微分方程有着深刻而生动的实际背景,是现代科学技术中分析问题与解决问题的一个强有力的工具。本文借助矩阵和微分方程的有关结论,给出了n阶线性非齐次微分方程初值问题的矩阵解法。

0 预备知识

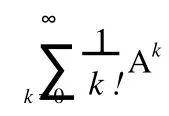
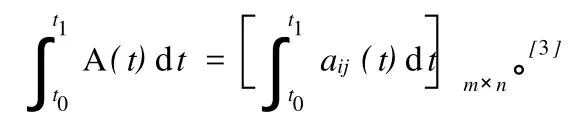
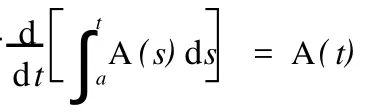
定义4设 a1(t),a2(t),…,an(t),u(t)均为[a,b]上连续的已知函数,且 u(t) ≠0,则称 yn+ a1(t)y(n-1)+ a2(t)y(n-2)+…+an(t)y=u(t)为n阶线性变系数非齐次微分方程。称 yn+a1(t)y(n-1)+a2(t)y(n-2)+…+an(t)y=0为n阶线性变系数齐次微分方程。[4]

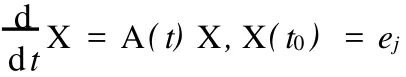
1 n阶线性非齐次微分方程初值问题的矩阵解法

证明 将X中每个分量xi(t) (i=1,2,…,n)展开为Maclaurin级数得:

[1] 程云鹏.矩阵论[M].西安:西北工业大学出版社, 1999:149-150.

[2] 李新,何传江.矩阵理论及其应用[M].重庆:重庆大学出版社,2005:96.

[3] 刘丁酉.矩阵分析[M].武汉:武汉大学出版社,2003:199.

[4] 王高雄,周之铭,朱思铭,等.常微分方程[M].2版.北京:高等教育出版社,1983:102-105.

[5] Gene H Golub,charles FVan Loan.Matrix Computations [M].Baltimore:The Johns Hopkins University Press, 1983:107-124.

[6] 宣立新.高等数学:上册[M].北京:高等教育出版社. 2002:191192.

(责任编校:夏玉玲)

A Matrix Solution to Differential Equation Initial Value Question of n Steps Wrong Uniform Number Linear Constant Index

CAO Yu-ping
(Department of Basic Courses,Lianyungang Vocational and Technical College,Lianyungang 222006,China)

A matrix solution has been worked out to n-step linear nonhomogeneous differential equation initial value by means of matrix index function and the concept of state shift matrix as w ell as the relevant conclusions regarding linear algebra and differential equation.

linear nonhomogeneous differential equation;initial-value question;matrix solution

O175

A

1672-349X(2010)06-0017-03

2010-07-01

曹玉平(1963-)男,副教授,主要从事工程数学的教学和研究。