柯西中值定理的中间点总位于区间正中间的函数类
时统业
(海军指挥学院 浦口分院,江苏 南京 211800)
柯西中值定理的中间点总位于区间正中间的函数类
时统业
(海军指挥学院 浦口分院,江苏 南京 211800)
给出使柯西中值定理的中间点总位于区间正中间的函数类.
柯西中值定理;导数;积分;中间点;充要条件
本文中c1,c2,c及qi均表示任意常数.

则 f"(x)g'(x)-f'(x)g"(x)=c
证 (1)式可化为

两边对h两次求导得

移项得

由洛必塔法则并注意到f(x)和g(x)有直到三阶的连续导数,得

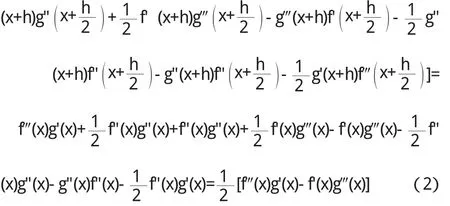
另一方面,
联合法是将冷却结晶法和酸沉法结合起来,从正钼酸铵溶液中析出高质量的七钼酸铵产品的一种方法。此法包括四钼酸铵氨溶、正钼酸铵溶液冷却结晶、母液酸沉三个过程。

比较(2)、(3)知必有f‴(x)g'(x)-f'(x)g‴(x)=0,即[f"(x)g'(x)-f' (x)g"(x)]'=0,故存在常数c使f"(x)g'(x)-f'(x)g"(x)=c.
引理2设φ(x)在区间I内有连续的二阶导数,且φ(x)≠0,φ"φ-(φ')2=c,则
φ(x)=q1x+q2或φ(x)=q1eq3x+q2e-q3x或φ(x)=q1c o s q3x+q2s i n q3x.证因φ"φ'2-c=0故


引理3设f(x)和g(x)在区间I内有连续的导数,且g'(x)≠0,a∈I,

则对任意h≠0,x∈I,x+h∈I,(1)式成立当且仅当

证 在(4)式两边在以a和x为端点的区间上积分,应用分部积分公式得

代入(1)式并整理即可得到(5)式.

证 充分性 由引理3,只要验证(3)式成立,这里略去验证过程.
必要性由引理1知,当(1)式成立时就有f"(x)g'(x)g"(x) =c1.于是,


由引理3,(5)式成立.
(5)式两边对h求导并整理得

(5)式两边对X求导并整理得

(6)-(7)得
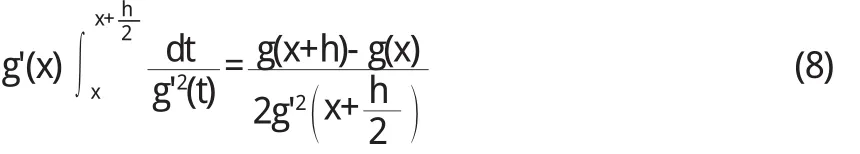
(8)式两边对h求导得

整理得

对g(x)和g'(x)引用引理1得g‴(x)g'(x)-(g"(x))2=c.令φ(x) =g'(x),则φ(x)≠0,且φ"φ-φ'2=c.
由引理2,φ(x)=q1x+q2或φ(x)=q1eq3x+q2e-q3x或φ(x) =q1c o s q3x+q2s i n q3x.故g(x)=q1x2+q2x+q3或g(x)=q1eq4x+q2e-q4x+q3或g(x)=q1s i n q4x+q2c o s q4x+q3.
在定理中取g(x)=x则得
推论 设f(x)在区间I上有连续的三阶导数,则对任意h≠0,x∈I,x+h∈I,成立

的充要条件是f(x)=q1x2+q2x+q3.
〔1〕苏化明,程海来.关于多项式的一个定理[J].高等数学研究,2005,8(5):33,38.
〔2〕李重华,孙薇荣,景继良,郑麒海.高等数学竞赛试题精解[M].上海:上海科学普及出版社,1996:7,43.
O172
A
1673-260X(2010)04-0001-02

