圆柱度误差的网格搜索算法
丁凤琴 薛国芳 雷贤卿
(①郑州旅游职业学院机电系,河南郑州 450009;②河南科技大学机电工程学院,河南洛阳 471003)
轴类零件是机械产品的重要组成部分,其精度的高低对产品的质量及其使用寿命至关重要,而衡量轴类零件形状误差大小的主要指标是圆柱度误差。圆柱度误差是具有四维描述变量的形状误差,其评定比较困难。通常的方法是建立测点到基准圆柱面的距离函数,然后根据国标定义的4种评定方法:最小二乘法、最小区域法、最小外接圆柱法和最大内接圆柱法(国标有阐述),构造相应的目标函数进行优化求解。而在优化求解的过程中,优化算法的选用至关重要,算法的收敛速度、求解精度和可靠性等因素直接关系到圆柱度的评定精度。
由于这些评定方法的目标函数是非线性的,优化的参数也比较多,有的在原理上就存在缺陷,如最小二乘法。为寻求符合定义的、最接近理想值的算法,本文介绍一种不需要优化算法,直接调用点至空间直线的距离公式及简单的判断即可得到圆柱度误差的算法——网格搜索算法。
1 圆柱度误差网格搜索算法的原理及步骤
1.1 网格搜索算法原理
评定圆柱度误差的基本原则是最小条件,符合最小条件准则的评定方法的核心内容就是要根据被测圆柱轮廓上点的坐标解算出包容实际轮廓的理想圆柱面的轴线参数,理想圆柱面的轴线位置应符合最小条件。以上所述四种评定方法中除最小二乘法外,其余三种是符合评定准则的。最小二乘法评定圆柱度误差是用最小二乘函数拟合被测圆柱面上的点,得到一条最小二乘轴线,然后求出被测圆柱面上各点到最小二乘轴线的距离,以距离最大值、最小值分别构造两个同轴圆柱面,这两个圆柱面之间的区域就是最小二乘法圆柱度误差。由于最小二乘轴线是在各测点距该理想圆柱面的轴线的径向距离与理想圆柱面半径之差的平方和为最小的条件下得来的,因此它不是符合最小条件的理想轴线,其评定准则与最小条件的定义相违背,在原理上存在缺陷,故得到的圆柱度误差不是很精确。尽管二乘轴线的位置不符合最小条件,但它是唯一的,用最小二乘法评定的圆柱度误差值也是唯一的。网格搜索算法是在最小二乘法基础上,在最小二乘轴线的周围(理想轴线一定在它周围)搜索符合最小条件的理想圆柱面轴线,即以最小二乘轴线为参考轴线,在其周围的一定区域内布置一直线群,其中必有一条直线最接近理想柱面的轴线,然后计算圆柱面上各测点到这一直线群(假定理想轴线)的每条直线的距离,从计算结果中进行分析判断寻找符合最小条件的理想轴线,然后,可分别按最小外接圆柱法、最大内接圆柱法和最小区域法计算圆柱度误差,网格搜索算法就是基于这种原理提出的。
1.2 网格搜索算法步骤
设圆柱面上各测点的坐标Pij(xij,yij,zj),被测圆柱面最小二乘轴线与坐标平面XOY的交点坐标为(a,b,0),方向数为(P,Q,1)。
(1)计算圆柱面上各测点Pij(xij,yij,zj)至最小二乘轴线的距离(最小二乘法)

式中,i为截面上的测量点,i=1,2…,N;j为测量截面,j=1,2,…,M。
(2)计算最小二乘圆柱度误差
找出Rij中的最大值Rmax、最小值Rmin,则被测圆柱面最小二乘法圆柱度误差值为

(3)计算最小二乘轴线与测量起始、终止截面的交点坐标
由被测圆柱面最小二乘轴线方程:(x-a)/P=(y-b)/Q=z可知,最小二乘轴线与测量起始截面(XOY坐标平面)的交点坐标T0(X0,Y0,Z0)、终止截面(Z=ZM平面)的交点坐标TM(XM,YM,ZM)分别为

(4)构造假定理想轴线
如图1,以端点T0(X0,Y0,Z0)为参考点,在XOY平面内设置一小正方形,其边长为最小二乘圆柱度误差ΔF,将该正方形的边长n等分,对边等分点两两连线构成网格点形式,那么各网格点的坐标dhk(xh,yk,z0)为

式中,h为z=0平面内x轴方向的网格点;k为z=0平面内y轴方向的网格点。
同理,以端点TM(XM,YM,ZM)为参考点构造的网格点的坐标elm(xl,ym,zm)为

式中,l为z=ZM平面内x轴方向的网格点;m为z=ZM平面内y轴方向的网格点。
这样在z=0,z=ZM平面内分别构造了n×n个网格点(如图1)。
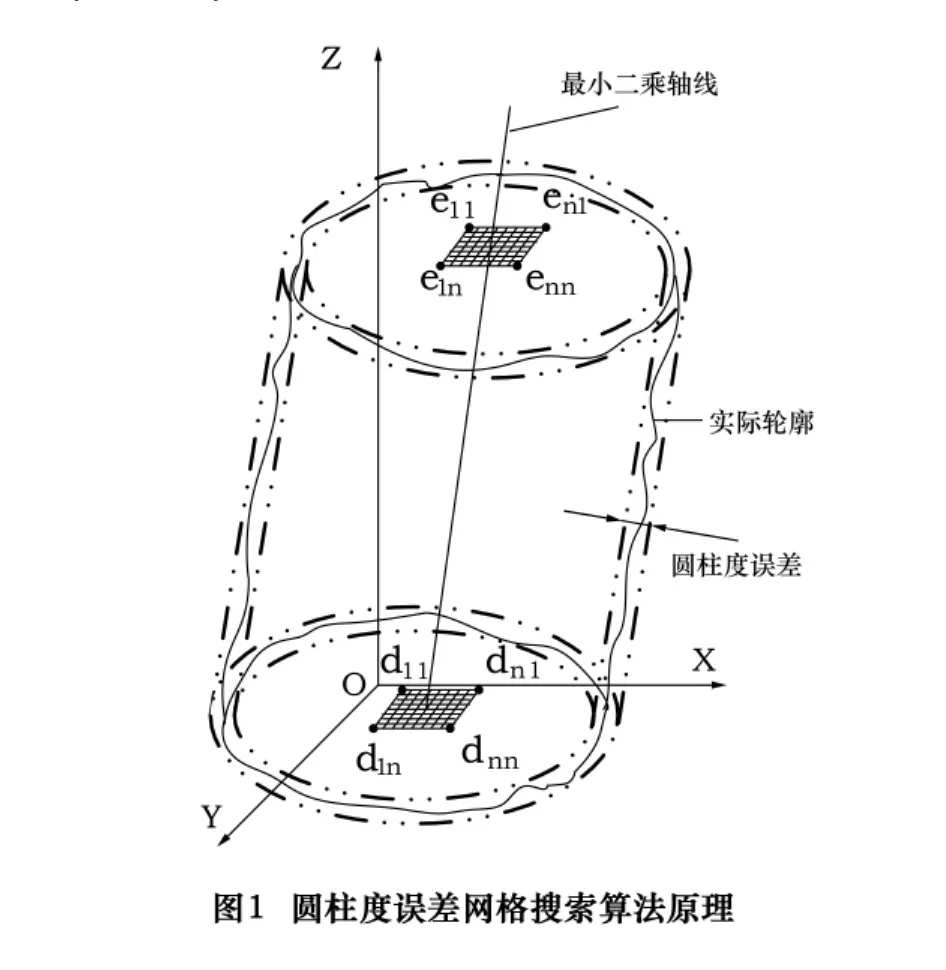
依次以初始测量截面(z=0平面)上的网格点dhk(xh,yk,z0)为假定理想轴线的起始点,遍历终止测量截面(z=ZM平面)上的网格点elm(xl,ym,zm),构造一簇轴线(共n4条直线),那么这些轴线的方向数为
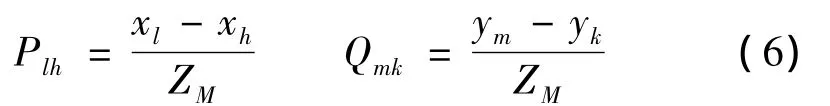
(5)按下式计算圆柱面上各测点Pij(xij,yij,zj)到一簇轴线(假定理想轴线)的距离

(6)寻找圆柱面上各点至每一条理想轴线的最大值、最小值以及极差
由于圆柱面各点至一簇轴线中的任一条轴线的距离中,都存在最大值、最小值和极差(最大值与最小值之差),因而可以得到n4个最大值、最小值和极差。
(7)计算最小外接圆柱法圆柱度误差
比较所有的最大值,其最小者即为最小外接圆柱的半径,用符号Rout表示;此最小者所对应的xh,yk,Plh,Qmk即为最小外接圆柱面轴线的参数,与此轴线参数相对应的由式(7)计算出来的最小值用符号rout表示。则最小外接圆柱法圆柱度误差值为

(8)计算最大内接圆柱法圆柱度误差
比较所有的最小值,其最大者即为最大内接圆柱的半径,用符号rin表示;此最大者所对应的xh,yk,Plh,Qmk即为最大内接圆柱面轴线的参数,与此轴线参数相对应的由式(7)计算出来的最大值用符号Rin表示。则最大内接圆柱法圆柱度误差值为

(9)计算最小区域法圆柱度误差
比较所有的极差值,其最小者即为最小区域,用符号ΔRarea表示,则最小区域法圆柱度误差值为

1.3 圆柱度误差网格搜索算法的解释
在最小二乘轴线的两端点周围布置了n2个网格点,如将最小二乘轴线上下两端点周围的网格点两两连线,将会产生n4条轴线,如将网格点分的足够细,必有一条轴线与理想轴线最接近或者重合。因而,网格搜索法实际上是一种穷举法。
圆柱面上的所有测点至其中一条轴线的距离中,总有最大值,最小值和极差(最大值与最小值之差),由于上下网格的连线有n4条,那么就有n4个最大值、最小值和极差。
若用最小外接圆柱法来评定圆柱度误差,则需要在这些最大值中找出最小者,此最小者即为符合最小外接圆柱评定法定义的最小外接圆柱面,其对应的那条网格连线即为被测圆柱面的理想轴线,以此网格连线为轴线构造的、能包容实际被测圆柱面的两个同轴圆柱面之间的径向距离即为最小外接圆柱法圆柱度误差。
若用最大内接圆柱法来评定圆柱度误差,则需要在这些最小值中找出最大者,此最大者即为符合最大内接圆柱评定法定义的最大内接圆柱面,其对应的那条网格连线即为被测圆柱面的理想轴线,以此网格连线为轴线构造的、能包容实际被测圆柱面的两个同轴圆柱面之间的径向距离即为最大内接圆柱法圆柱度误差。
若用最小区域法来评定圆柱度误差,则需要在这些极差值中找出最小者,此最小者即为符合最小区域法定义的最小区域法圆柱度误差。
以上得到的网格连线与被测圆柱面的理想轴线的接近程度与等分点数及截面上布置的正方形边长有关,边长值越小、等分点数越多,计算出来的圆柱度误差值就越接近于真值,但边长值太小有可能构造的网格连线不能包含被测圆柱面的理想轴线,等分点数过多会导致计算量大,影响计算速度。为提高计算速度和测量精度,可进行多次循环。先以最小二乘法圆柱度误差值为边长,等分点数取少一些(例如,取n=10),然后以计算出的圆柱度误差(最大外接圆柱法、最小内接圆柱法、最小区域法)中的最大值为边长,布置更细的网格,重复上述步骤,当最小极差与次最小极差非常接近(如小于0.000 1 μm)时,可以认为此时的最大值中的最小者为最小外接圆柱法圆柱度误差,最小值中的最大者为最大内接圆柱度误差,极差中的最小者为最小区域法圆柱度误差。其计算过程流程图如图2。
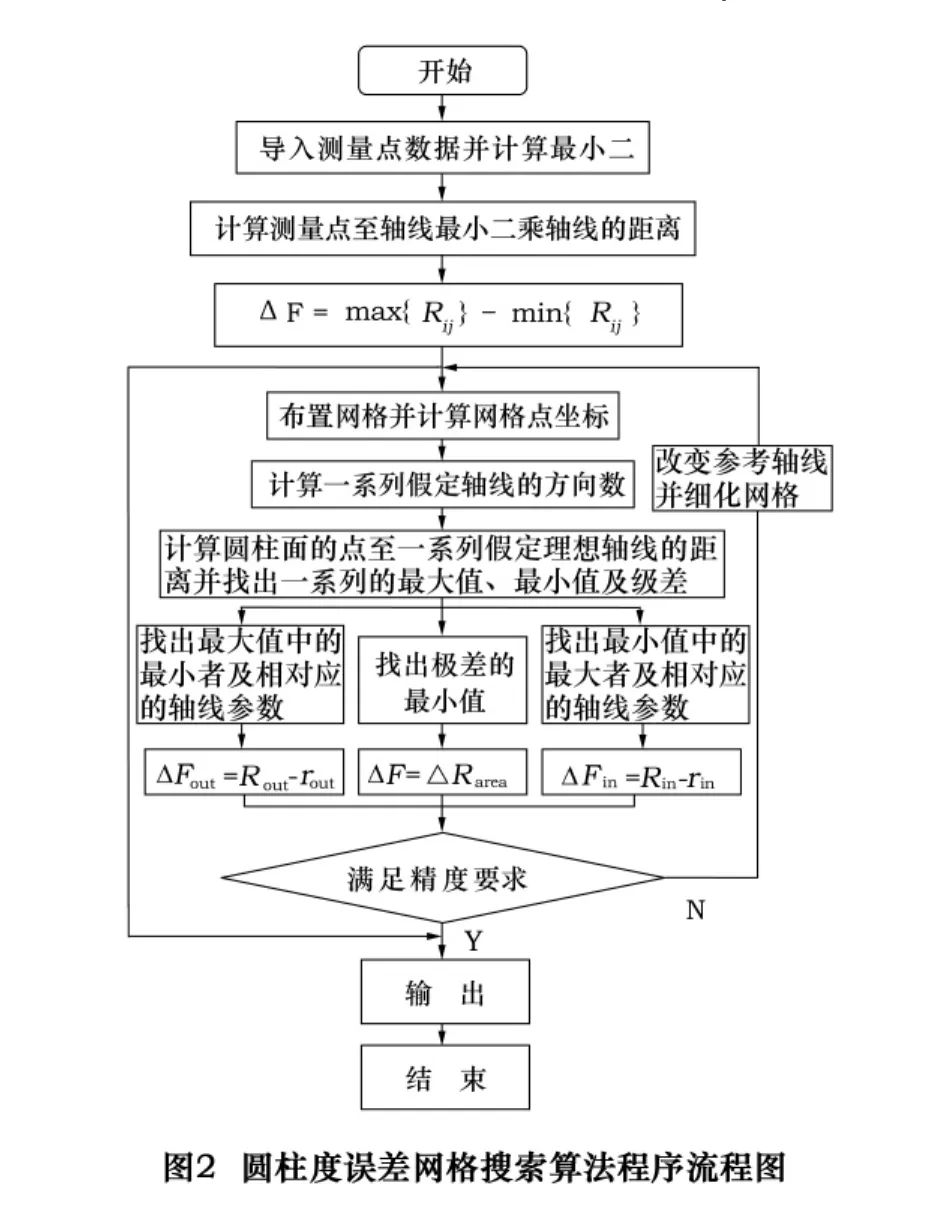
2 圆柱度误差网格搜索算法仿真
按以上所述的原理与步骤,对圆柱体圆柱度误差进行网格搜索算法仿真,仿真结果与预先设定的完全一致,说明圆柱度网格搜索算法可以实现圆柱度误差的有效评定。
3 结语
网格搜索算法是解决圆柱度误差精确评定问题的新思路,是计量测试技术中形位误差评定的一全新手段,通用性强,可以达到完全实用的程度。
圆柱度误差的网格搜索算法简单直观,并且符合圆柱度误差的评定定义,不需要将点到直线(平面、空间)的公式线性化,也不需要确定优化步长和优化方向,算法简单直观。但在测量点较多时,计算量比较大。
依据该算法设计出的圆柱度误差评定软件可以很容易地安装到圆度测量仪、三坐标测量机和其它带有计算机的测试仪器上,能够满足圆柱度误差的精确评定。
[1]李惠芬,蒋向前,张玉,等.直角坐标系下计算圆柱度误差的一种实用算法[J].仪器仪表学报,2002,23(4):424-426.
[2]温秀兰,宋爱国.基于改进遗传算法评定圆柱度误差[J].计量学报,2004,25(2):115 -118.
[3]Lai HY,Jywe WY,Chen CK,et al.Precision modeling of form error for cylindricity evaluation on using genetic algorithms[J].Precision Engineering,2000,24(4):310-319.
[4]Y.Z.Lao,H.W.Leong,F.P.Preparata Singh.Accurate cylindricity evaluation with axis- estimation preprocessing[J].Precision Engineering,2003,27(4):429 -437.
[5]刘国光.基于Matlab评定圆柱度误差[J].工程设计学报,2005,12(4):236-239.
[6]Hossein Cheraghi,Guohua Jiang,Jamal Sheikh Ahmad .Evaluating the geometric characteristics of cylindrical features[J].Precision Engineering,2003,27(2):195 -204.
[7]陈立杰,张镭,张玉.直角坐标采样时的圆柱度误差数学模型[J].东北大学学报:自然科学版,2005,26(7):676 -679.

