提高数控系统基准脉冲直线插补速度及精度的研究*

范希营 郭永环

(徐州师范大学机电工程学院，江苏徐州 221116)

为提高插补精度，简化运算程序，扩大逐点比较法的应用范围，国内外许多学者研究了各种改进方法［1～9］，为经济型数控系统的发展做出了卓越的贡献。但是有的成果进给速度提高了，而逐点比较法其误差小于1个脉冲当量的误差较大的问题没有得到改善;有的插补精度提高了，但是算法复杂，进给速度却降低了;也有的虽然插补精度和进给速度都得到提高，但x轴、y轴脉冲分配很不均匀，造成加工后的表面粗糙。本文提出一种新型基准脉冲插补原理，旨在解决上述问题。

1 传统的逐点比较法存在的不足

(1)传统的逐点比较法进给速度不够快。用逐点比较法对直线进行插补应走的总步数较多，生产效率较低;

(2)沿X、Y坐标轴脉冲分配不均匀。造成系统平稳性差，使加工后的表面粗糙，加工质量降低;

(3)进给误差较大。进给误差小于一个脉冲当量，使加工精度不高。

2 新型基准脉冲插补原理

2.1 新型基准脉冲插补思想

在各种改进的基准脉冲插补方法中，较有名的就是最小偏差法和半步偏差法［8，9］，但这两种方法均以和的形式构造二次偏差判别函数，二者均是在试算两个插补方向上的偏差之后再比较其绝对值的大小，使算法变得复杂，执行速度降低。本文所提出的新型插补算法，以差的形式构造偏差函数，将偏差计算与偏差比较合并考虑，直接递推偏差比较结果，使算法大为简化，插补运算速度提高一倍左右。

2.2 新型基准脉冲插补原理

2.2.1 插补原理

以0<α<45°区间内直线OL为例，如图1所示，直线起点坐标为(0，0)，终点坐标为(xe，ye)，则可知直线方程为y=(ye/xe)x，取F=xey－yex为偏差函数 。

设当前有一插补点P(xi，yi)位于直线OL下方，xe>ye。根据速度条件可排除仅走Δx的走步方式，则第i+1步有两个可能的插补点:Ai(xi+1，yi);Bi(xi+1，yi+1)。其中xi+1=xi+1，yi+1=yi+1。则新插补点和理想直线的偏差分别为

由于 Δ(Ai)、Δ(Bi)均大于0，显然:

1.4疗效判定标准:①显效:患者的心功能改善超过II级,肝脏缩小2cm以上。②有效:患者的心功能改善I级,症状体征均缓解。③无效:患者的心功能改善不足,体征和症状没有明显变化。治疗总有效率=(显效+有效)例数/总例数×100%。

(1)若 Δ(Ai)－Δ(Bi)>0，则 Δ(Ai)>Δ(Bi)，根据下一插补点距理想直线的偏差应最小的原则，此时应向B点(+Δx，+Δy)方向进给;

(2)若 Δ(Ai)－Δ(Bi)<0，则 Δ(Ai)<Δ(Bi)，此时应向A点(+Δx)方向进给;

(3)若 Δ(Ai)－Δ(Bi)=0，则 Δ(Ai)=Δ(Bi)，此时向A点或B点方向进给均可，本文约定向(+Δx)方向进给。

故可构造一插值偏差函数f，令

则 :当fi<0时，向(+Δx)方向进给;

当fi≥0时，向(+Δx，+Δy)方向进给。

2.2.2 偏差计算

由式(3)有:

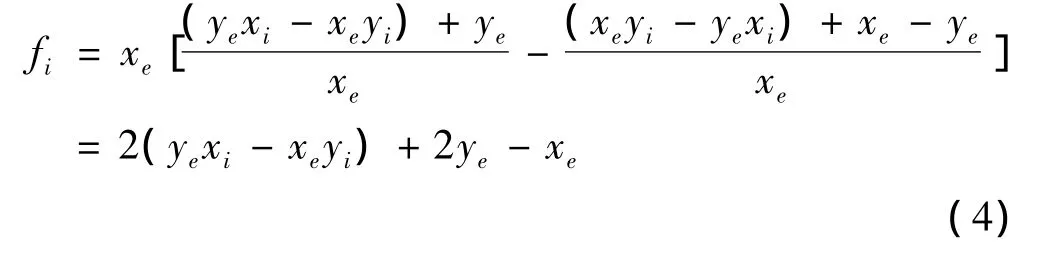
(2)当fi≥0时，应向(+Δx，+Δy)方向进给，xi+1=xi+1，yi+1=yi+1

2.2.3 终点判别

终点判别式为插补起始状态值与插补步数之差为零，即:Σi+1=0

起始状态值:Σ0=xe+ye;

例如，当向(+Δx，+Δy)方向进给时，:Σi+1=Σi－2;当向(+Δx)方向进给时，Σi+1=Σi－1;

由初值式(7)起应用递推公式(5)或(6)迭代至Σi+1=0，即完成该直线插补运算，与最小偏差法、半步偏差法相比，避免了两个插补方向的偏差试算及绝对值大小比较，而是将其归于一式，直接递推偏差比较结果，每步插补仅需一次递推计算，使算法大为简化。

2.3 新型插补算法流程图

新型插补算法在第一象限内插补运算流程图如图2所示。

3 新型基准脉冲插补轨迹及脉冲分配

3.1 新型基准脉冲插补轨迹及脉冲分配图

例如，利用新型插补算法加工一直线OL，起点坐标为(0，0)，终点坐标为(28，16)，则改进前、后逐点比较法直线插补轨迹如图3所示，改进前、后逐点比较法脉冲分配对比图如图4所示。

3.2 新型基准脉冲插补速度、脉冲均匀性及插补精度分析

(1)由图3可看出，传统逐点比较法插补了44次，而新型逐点比较法插补了28次，可见，改进后的新型插补算法使插补次数减少了16次，新型插补算法使插补速度提高30%以上。

(3)传统的逐点比较法插补偏差为0的步数有4步，插补偏差为0.124的步数有8步，插补偏差为0.248的步数有8步，插补偏差为0.372的步数有8步，插补偏差为0.496的步数有8步，插补偏差为0.620的步数有4步，插补偏差为0.744的步数有4步;而新型插补算法插补偏差为0的步数有4步，插补偏差为0.124的步数有8步，插补偏差为0.248的步数有8步，最大插补偏差0.372也为8步，可见脉冲分配较传统的逐点比较法均匀，且周期性变化小。

4 结语

以差的形式构造的偏差函数，将偏差计算与偏差比较合并考虑，可提高数控系统基准脉冲直线插补速度及精度。①可使插补精度提高一倍。②使插补速度提高30%以上。③使各坐标轴脉冲分配较均匀，且周期性变化小。

1 李文斌，李卫京，杨世春.一种快速实用的插补算法［J］.太原理工大学学报，2004(4):431～433

2 袁超廷.数控中的最佳插补原理——最小误差法［J］.重庆建筑工程学院学报，1985(5):86～98

3 苏秀平.细论直线的逐点比较法插补［J］.机床与液压，2004(4):119～121

4 Srinivasan V，Nackman LR.Voronoi diagram for multiplyconnected polygonal domains I:algorithm［J］.IBM Journal of Research and Development 1987，31(3):361 －372

5 Lai W，Faddis T，Sorem R.Incremental algorithms for finding the offset distance and minimum passage width in a pocket machining toolpath using the Voronoi technique［J］.J Mater Process Technol 2000;100(1):30－35

6 Kim K，Kim MK.Volumetric accurary analysis based on generalized geometric error model in multi axis machine tools［J］.Mechanisms and Machine Theory，1991(3):P207－219

7 Dorndorf U，Kiridena VSB.Optimal budgeting of quasistatic machine tool errors［J］.Journal of Engineering for Industry，1994，116(1):42－52

8 李恩林.最小偏差插补原理［J］.机械设计与制造，1980(1):19～26

9 齐从谦.半步偏差法插补的原理及实践［J］.安徽工学院学报，1982(2):23～33