一种三站时差定位的布站优化算法

(1.解放军电子工程学院，合肥 230037；2. 解放军61764部队，海南 三亚 572013)

1 引 言

三站时差定位是一种无源定位方法，利用目标位于地球表面的约束，结合三站分别对目标进行时差测量形成的两路时差数据，实现对目标的三维定位。因其具有无源被动工作、定位精度高[1-2]等优点，在雷达、无线通信定位[3]、水声定位[4]等领域得到了广泛应用。

对于时差定位系统，目标的定位误差是与目标相对于测量站的几何关系密切相关的[1,5]。因此，在时差测量误差及测量站站址误差等误差因素一定的情况下，对测量站布站进行优化，是提高定位精度的有效手段。目前的文献多是对时差定位精度与布站关系的研究，定性地选择某种布站形式为最优布站[5-6]。本文以提高一定的目标区域的整体定位精度为目标，运用基于多目标规划的最优化算法建立数学模型，构造最小最大评价函数，以使目标区的最大水平定位精度因子(HDOP)最小的布站为最优布站。

2 基本原理

2.1 定位模型

假设3个测量站在地心直角坐标系下的坐标分别为xi,yi,zi，i=0,1,2，接收来自位于地球表面某一坐标x,y,z的目标点信号，可以得两路时差数据对应于两个时差方程，联立WGS-84地球表面方程，即可建立目标点定位方程组[7-8]：

(1)

图1 三站时差定位系统示意图Fig.1 Schematic of the tri-station TDOA location system

2.2 多目标规划简介[9]

多目标规划是一种常见的最优化模型，相对于单目标规划问题，其有多个目标函数。数学模型为

minF(X)=min[f1(X),f2(X),…,fn(X)]
s.t.G(X)≤0

(2)

式中，X=[x1,x2,…,xm]为决策变量；G(X)=[g1(X),g2(X),…,gp(X)]为约束条件；gi(X)(i=1,2,…,p)可以是线性函数，也可以为非线性函数，当p=0时，为无约束多目标规划。

3 水平定位精度因子(HDOP)

定位精度是定位系统最重要的指标之一。这里，以水平定位精度因子(HDOP)作为定位精度的度量准则。

对式(1)的前两式两边取微分可得[8]：

c·dΔti+ui·dXi-u0·dX0(i=1,2)

(3)

其中：

对式(1)最后1式两边微分[8]：

(4)

其中：

k=1/(1-e2)2

结合式(3)与式(4)，有：

A·dX=c·dΔT+dU

(5)

其中：

由式(5)可得：

dX=A-1(c·dΔT+U)

设时差测量误差、各测量站位置误差均值为0，且不相关，则目标辐射源的定位误差协方差矩阵为

PdX=EdXdXT=

A-1c2EdΔTdΔTT+EdUdUTA-1T

(6)

式(6)得到的是地固直角坐标系中定位的三维定位误差协方差矩阵，考虑到一般对辐射源的定位精度指标是指在大地坐标下的经纬高的误差。因此需将此协方差矩阵转换到大地坐标下[10]：

PdL=J·PdX·JT

(7)

其中：

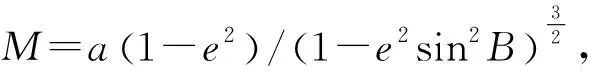
式(7)中PdL中PdL(1,1)、PdL(2,2)分别为经度、纬度分量的定位误差方差，将其转换为距离的方差分别为RL、RB。

定义水平方向的定位精度因子：

(8)

以此HDOP值作为定位精度的度量准则。

4 基于多目标规划的布站优化

4.1 布站优化原则

这里考虑的布站优化问题是在一定的布站区域里，合理布设3个测量站的位置，使定位系统对于一定目标区域的整体定位精度达到最优。因此，布站优化问题主要考虑以下几点原则：

(1)3个测量站要布设在一定的布站区域内；

(2)3个测量站之间的距离满足通视条件；

(3)3个站的覆盖范围均能覆盖整个目标区域；

(4)使定位系统对目标区域的整体定位精度最优。

4.2 布站优化问题的多目标规划评价函数构造

对于多目标规划问题，其求解的主要思路是设法将多目标问题转化为单目标问题，然后以单目标规划的求解方法求解，而转化的关键是依据决策者的需求，合理构造评价函数[9]。

结合4.1节提出的布站优化问题需考虑的原则，这里选择最小最大(minimax)法构造评价函数。这种决策方法是采取稳妥的保守策略，即在最坏的情况下，寻求最好的结果。按照此策略，构造如下评价函数：

φ(X)=max[f1(X),f2(X),…,fn(X)]=

(9)

这样，就将多目标规划问题转化为单目标规划问题，目标函数可写为

(10)

式中，D=X|G(X)≤0，为决策变量的可行域。

4.3 基于多目标规划的布站优化

按照4.2节介绍的最小最大评价函数构造法，可将基于多目标规划布站优化问题，写成如下的数学模型。

假设目标区域范围为：经度方向区间lmin,lmax；纬度方向区间wmin,wmax；三站高度相同，均为h。

目标函数：

min{max[HDOP1(X),HDOP2(X),…,HDOPn(X)]}=

(11)

其中，X=[l1,w1,l2,w2,l3,w3]为决策变量；li(i=1,2,3)为待优化3个测量站经度；wi(i=1,2,3)为纬度；n表示将目标区域按一定规则划分为n部分，当n足够大时，可认为目标区域由n个目标点构成。

HDOPi(X)(i=1,2,…,n)表示三站坐标为某X=[l1,w1,l2,w2,l3,w3]时，对第i个目标的水平定位精度因子的大小。

约束条件[11]：

(12)

其中：

上述布站优化模型基本思想是使目标区域内最大的定位误差(这里为HDOP)最小，这样就可以保证目标区域的整体定位精度，同时，附加约束条件，以满足4.1节提出的布站优化原则。

求解上述模型的算法是对布站区域内的每一种布站形式进行循环搜索，对于每一种布站形式首先判断其是否满足约束条件，若不满足，则直接进入下一种布站形式的搜索判断；若满足，则计算其对目标区域内所有点的HDOP值，取其中最大的HDOP值，并记录相应的布站形式(决策变量X，即各测量站坐标)。而后进入下一种布站形式的计算，如此循环，取所有保存的最大HDOP值最小的一种布站形式为满足要求的最优布站。

5 仿真分析

仿真实验假设目标区域的范围为东经121.4°～122.6°，北纬22.0°～22.8°，目标高程为0；布站区域的范围为东经121.0°～123.0°，北纬23.0°～24.0°，高程2 000 m。

将目标区域按经、纬度步长均为0.05°划分为n′个区域：

n′=[(122.6-121.4)/0.05]×

[(22.8-22.0)/0.05]=24×16

则可取n=25×17=425个点表示整个目标区域。

同样将布站区域按照经、纬度步长均为0.000 01度划分为m′个区域：

m′=[(123.0-121.0)/0.00001]×

[(24.0-23.0)/0.00001]=

200000×100000

则可取m=200001×100001种布站形式。

取满足约束条件的初值X0：

X0=[122.300,23.050,121.600,23.080,

121.950,23.125]

运用上述基于多目标规划的布站优化方法，对m种布站形式逐一搜索判断，可得优化结果X*：

X*=[122.920,23.000,121.080,23.000,

122.054,23.467]

设定位系统的时差测量误差为10 ns，测量站在大地直角坐标系下x、y、z各方向误差均为5 m。图2～4分别为所设初值X0对应的HDOP等值线分布图、最优布站X*的HDOP等值线分布图及覆盖范围。图中五角星表示3个测量站的位置，阴影区域表示目标区域，由三角形围成的矩形框表示布站区域的范围。图2和图3中曲线为HDOP等值线，图4中曲线为三站各自的覆盖范围。

图2 布站初值的HDOP等值线分布Fig.2 Distribution of HDOP isoline of the initial station layout

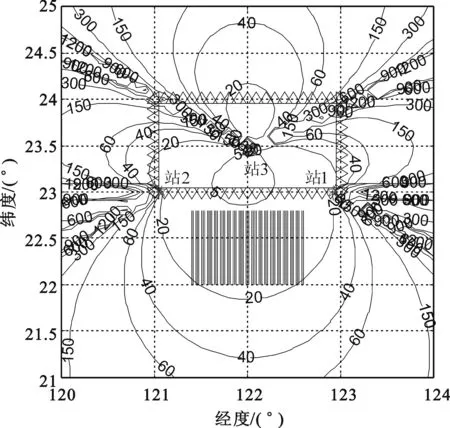
图3 优化布站的HDOP等值线分布Fig.3 Distribution of HDOP isoline of the optimal station layout

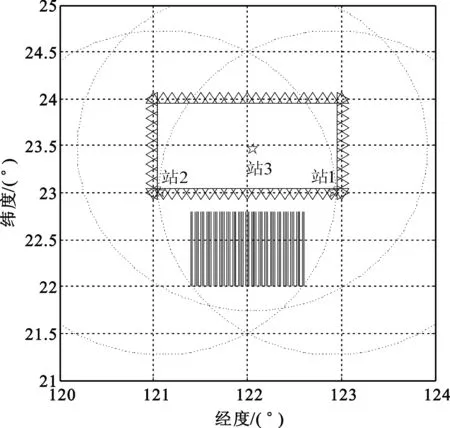
图4 优化布站的覆盖范围Fig.4 Overlay range of the optimal station layout

由图2～4可以看出，与所设初值，即初始布站形式相比，运用基于多目标规划的布站优化方法所得的布站优化结果，目标区域的整体定位精度明显提高，同时又保证了测量站对整个目标区域的覆盖。

6 结束语

本文以水平定位精度因子(HDOP)为定位精度的度量准则，基于提高定位精度的考虑，提出了一种基于多目标规划的三站时差定位布站优化方法。仿真结果表明，运用该方法对测量站布站进行优化，效果明显，既能保证系统覆盖范围、各站间通视等约束条件，同时又能使目标区域的整体定位精度达到最优。在实际应用中，可根据经验信息，各站可设不同的小范围搜索区域，以提高优化运算效率。

参考文献：

[1] 孙中康, 周一宇, 何黎星. 单多基地有源无源定位技术[M]. 北京: 国防工业出版社, 1996:181-195.

SUN Zhong-kang, ZHOU Yi-yu, HE Li-xing. Mono-static, multi-static active and passive location techniques[M]. Beijing: National Defense Industry Press, 1996:181-195.(in Chinese)

[2] 朱庆厚. 到达时间差 ( TDOA)测向定位研究[J]. 电讯技术, 2007, 47(1): 53-56.

ZHU Qing-hou. Study on TDOA Direction Finding and Location Measurement [J]. Telecommunication Engineering, 2007, 47(1): 53-56. (in Chinese)

[3] Caffery J J. Wireless Location in CDMA Cellular Radio Systems [M]. [S.l.]：Kluwer Academic Publishers, 1999.

[4] Chan Y T, Ho K C. A Simple and Efficient Estimator for Hyperbolic Location [J]. IEEE Transactions on Signal Processing,1994,42(8):1905-1915.

[5] 钱镱,陆明泉,冯振明.基于TDOA原理的地面定位系统中HDOP的研究[J].电讯技术,2005,45(4):135-138.

QIAN Yi,LU Ming-quan,FENG Zhen-ming.Research on the HDOP of a TDOA Land-Based Positioning System [J].Telecommunication Engineering,2005,45(4):135-138.(in Chinese)

[6] 王成, 李少洪, 黄槐. 测时差定位系统定位精度分析与最优布站[J]. 火控雷达技术, 2003, 32(1): 1-6.

WANG Cheng,LI Shao-hong,HUANG Huai.Location Accuracy Analysis and Optimal Distribution of TOA Difference Location System [J].Fire Control Radar Technology,2003,32(1):1-6.(in Chinese)

[7] 谢恺, 钟丹星, 邓新蒲,等. 一种空间时差定位的新算法[J]. 信号处理, 2006, 22(2): 129-135.

XIE Kai, ZHONG Dan-xing, DENG Xin-pu,et al. A new algorithm for the time difference location in aerospace [J]. Signal Processing, 2006,22(2):129-135. (in Chinese)

[8] 钟丹星,邓新蒲,周一宇.基于WGS-84椭球模型的卫星测时差定位精度分析[J].电子对抗技术,2002,17(5):18-21.

ZHONG Dan-xing, DENG Xin-pu, ZHOU Yi-yu. Precision Analysis of Satellites DTOA Location Based on WGS-84 Ellipsoid Model[J].Electronic Warfare Technology, 2002, 17(5): 18-21. (in Chinese)

[9] 阳明盛, 罗长童. 最优化原理、方法及求解软件[M]. 北京: 科学出版社, 2006: 90-92.

YANG Ming-sheng, LUO Chang-tong. Optimization theory, methods and software [M]. Beijing: Science Press, 2006: 90-92. (in Chinese)

[10] 边少锋, 李文魁. 卫星导航系统概论[M]. 北京: 电子工业出版社, 2005: 22-27.

BIAN Shao-feng, LI Wen-kui. Introduction to Satellite Navigation Systerm [M]. Beijing: Publishing House of Electronics Industry, 2005: 22-27. (in Chinese)

[11] 丁鹭飞，耿富录. 雷达原理[M]. 西安: 西安电子科技大学出版社, 2002: 158-160.

DING Lu-fei, GENG Fu-lu. Radar Theory [M]. Xi′an: Xidian University Press, 2002: 158-160. (in Chinese)