新旧规范对预应力连续刚构桥线形影响分析

黄雅宁，周水兴，王 艳，曹 帅

(重庆交通大学土木建筑学院，重庆 400074)

预应力混凝土连续刚构桥是大跨径桥梁中经常采用的一种结构型式，因其行车舒适性好、外形优美等特点在国内大量建造，但近年来发现按JTJ 023—85《公路钢筋混凝土及预应力混凝土桥涵设计规范》设计的连续刚构桥，不少出现了运营期挠度过大和箱梁开裂等问题。该规范自2004年起，已从半经验半概率的极限状态设计方法过渡到以概率极限状态设计方法［1］，即由 JTJ 023—85《公路钢筋混凝土及预应力混凝土桥涵设计规范》(以下简称《85规范》)过渡到JTG D 62—2004《公路钢筋混凝土及预应力混凝土桥涵设计规范》(以下简称《2004规范》)。

《2004规范》对《85规范》做了较大的改进，不仅引入了结构重要性系数、挠度长期增长系数ηθ等概念，而且还修改了徐变计算模式，对混凝土抗裂验算要求也有提高，这些修改直接影响到预应力混凝土连续刚构桥的桥面线形。文献［2－3］按照新旧规范中的徐变计算公式，分析了考虑或不考虑徐变对预应力混凝土连续刚构桥施工过程的挠度及应力的影响，认为箱梁混凝土的徐变对合拢前几个节段箱梁的挠度影响较大，用新旧规范分别计算出来的预拱度，中跨最大值有一定的差别，其余部分基本一致;文献［4－5］侧重于新旧规范在刚构桥设计内力方面的差异，但均未分析抗裂验算要求、刚度取值和预拱度计算公式不同对连续刚构桥线形的影响。

笔者结合阿蓬江大桥，综合考虑新旧规范在徐变计算模式、抗裂验算要求、刚度取值和预拱度计算公式等方面的不同对连续刚构桥线形的影响。结果表明:对于大跨度连续刚构桥，尽管抗裂验算中《2004规范》效应组合较《85规范》小，但由于预压应力要求的提高，使得最终预应力度并不减小，而徐变计算模式、刚度取值和预拱度计算公式等方面的修改，使得成桥运营状态挠度值比按《85规范》小，线形更加美观、合理。

1 工程概况

阿蓬江大桥为90 m+170 m+90 m三跨预应力混凝土连续刚构桥，箱梁根部高度10.5 m，跨中高度3.5 m;根部底板厚100 cm，跨中底板厚32 cm，箱梁高度以及箱梁底板厚度按1.8次抛物线变化。箱梁顶宽12.0 m，底宽6.5 m。采用桥梁博士系统3.0建立了阿蓬江大桥计算模型，桥面划分99个单元，桥墩划分为106个单元。如图1。

图1 阿蓬江大桥有限元模型Fig.1 Finite element model of A′Pengjiang Bridge

2 线形主要影响因素的分析

2.1 徐变计算模式及龄期不同

《2004规范》徐变计算龄期采用10 a，且徐变计算采用CEB-FIP 1990模式，该模式将徐变系数表达为一系列乘积的形式。徐变系数公式按式(1)计算:

式中:t、t0分别为混凝土的计算龄期和加载期;φ0为名义徐变系数;βc为加载后徐变随时间的发展系数;RH为环境平均相对湿度;h为混凝土构件理论厚度;RH0、fcm、fcm0、h0、t1的具体含义及取值见《2004规范》。

《85规范》徐变的计算龄期为1000 d(3 a)，徐变计算采用GEB-FIP 1978模式，该模式将徐变系数表达为若干个性质不同的分项系数之和。徐变系数按式(2)计算:

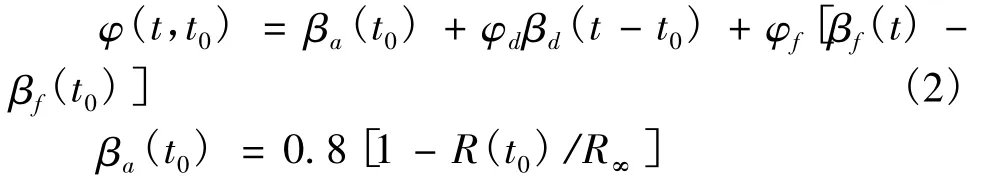
式中:φ(t，t0)为计算龄期为t时的混凝土徐变系数;φd为弹性滞后系数;βa(t0)、βd(t－t0)为随时间而增长的滞后弹性应变;R(t0)为加载时混凝土的强度;R∞为最终强度;φf为流塑系数，φf=φf1×φf2(φf1依周围环境而定的系数;φf2依理论厚度h而定的系数);βf(t)、βf(t0)随混凝土龄期而增长的之后塑性应变。

以1 m×1 m矩形截面构件为例，说明《85规范》与《2004规范》在计算徐变系数上的差异。分析中，加载龄期和计算龄期均取10 d和1000 d，h=50 mm，RH=70%。其余参数如下:《2004规范》中，h0=100 mm，βc=5，h=50 mm，RH0=100%，按式(1)计算，得徐变系数φ(t，t0)为1.95;《85规范》中，βf(t0) =0.23，βf(t) =0.78，φf2=1.85，φf1=2，R(t0)/R∞=1，βd(t－ t0)=1，βd(t0)=0，按式(3)计算，得徐变系数 φ(t，t0) 为 3.24，是《2004规范》的1.66倍。

2.2 抗裂验算要求不同

《2004规范》正截面抗裂对混凝土构件拉应力验算修改为:短期效应组合下预制构件 σst－0.85σpc≤0;分段浇筑或砂浆接缝的纵向分块构件σst－0.8σpc≤0。

对于短期效应组合下拉应力σst，修改了其效应的组合方式及其组合系数，提出了可变作用短期效应组合时的频遇系数和长期效应组合时的准永久值系数，从而导致短期效应组合、长期效应组合比《85规范》标准值组合要小。且《2004规范》又规定汽车荷载在抗裂验算中不计冲击系数，使得《2004规范》作用效应取值比《85规范》小得多。

为了不因效应组合的改变过多而降低预应力度，《2004规范》同时对混凝土构件的预压应力进行了修改，规定 σst－0.85σpc≤ 0，较《85规范》(σ －σh≤0)预应力混凝土构件正截面预压应力提高了15%;分段浇筑或砂浆接缝的纵向分块构件σst－0.8σpc≤0，较《85规范》(σ －σh≤0)预压应力提高了20%。

根据《2004规范》的统计，按荷载短期效应组合且汽车不计冲击系数与《85规范》荷载标准值组合且汽车计入冲击系数比较，前者为后者的(0.77～0.96)倍，但因《2004规范》中预压应力的提高和40 m以上梁桥抗裂验算新旧规范均不考虑汽车冲击系数，对于大跨径刚构桥按《2004规范》设计计算的预应力度较《85规范》有所提高。

2.3 刚度取值不同

《2004规范》对于预应力混凝土构件仍保留《85规范》的计算方法，只将其中的全截面抗弯刚度B0=0.85ECT0改为 B0=0.95ECT0，为《2004规范》的0.89倍，从而引起连续刚构桥长悬臂和成桥状态下的挠度计算值减小。

2.4 预拱度取值不同

《2004规范》预拱度计算引入长期增长系数，计算公式由《85规范》的=改为=ηθ()。式中:为结构自重引起的挠度;为收缩徐变引起的挠度;为可变频遇荷载引起的挠度;ηθ为挠度长期增长系数。阿蓬江大桥采用C50混凝土，故按《2004规范》6.5.3条直线内插取1.412。

以阿蓬江大桥为例，挠度长期增长系数乘以汽车荷载系数(1.412×0.35=0.49)，与《85规范》的取值0.5基本相同，而结构自重乘以1.412的长期增长系数使得预拱度值比《85规范》大。

3 线形结果比较

3.1 徐变计算模式与龄期

以《2004规范》所取的“3600 d”为计算龄期，按《2004规范》和《85规范》分别计算阿蓬江大桥成桥运营期徐变引起的挠度，同时按《85规范》规定的“1000 d”为龄期，计算由混凝土徐变引起的挠度，结果如图2。

图2 按两版本规范计算的收缩徐变挠度比较Fig.2 Comparison of deflection caused by shrinkage and creep between different specifications

从图2可以看出，《2004规范》和《85规范》在相同计算龄期(3600 d)得到的挠度趋势基本一致，《2004规范》计算得到的跨中峰值为11.1 cm，《85规范》计算跨中峰值为13.1 cm，最大相差2 cm。而按《85规范》计算1000 d龄期时的跨中变形仅为7.32 cm。显然，《85规范》以1000 d计算连续刚构桥挠度的龄期偏短，这也是导致目前连续刚构桥跨中下挠较大的一个重要原因。

3.2 抗裂验算要求

由于《2004规范》规定分段浇筑或砂浆接缝的纵向分块构件 σst－0.8σpc≤0较《85规范》(σ －σh≤0)预应力混凝土构件正截面预压应力有所提高，笔者以20%预压应力为差值对比阿蓬江大桥最大悬臂、成桥状态、运营10 a挠度计算结果，见图3～图5。

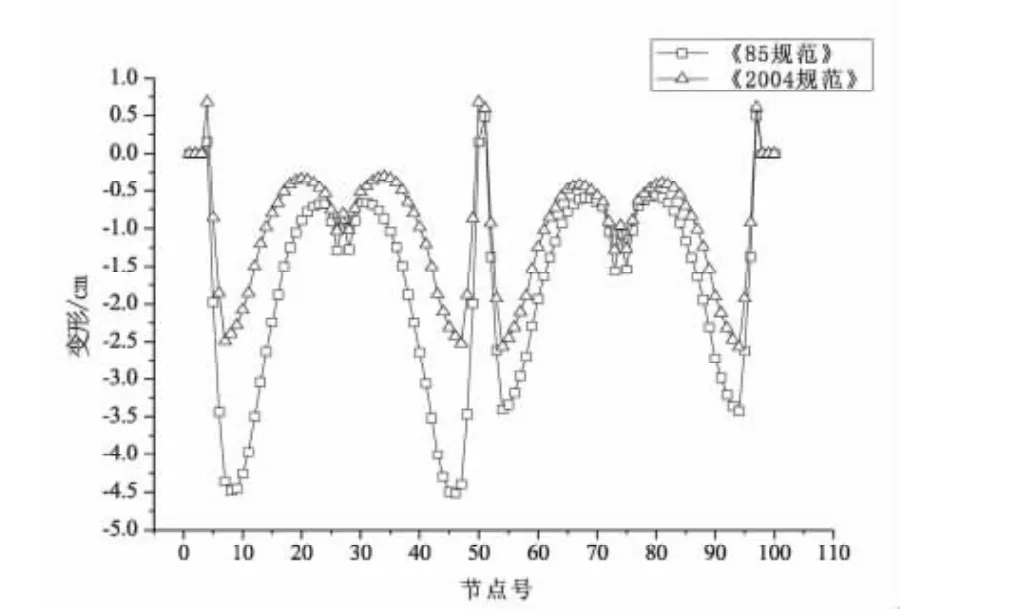
图3 按两版本规范计算的最大悬臂状态挠度比较Fig.3 Comparison of deflection in longest cantilevered stage between different specifications

从图3看出，《2004规范》和《85规范》预压应力折减0.8计算出的挠度趋势相同，《2004规范》计算出的最大挠度值为2.52 cm，而《85规范》计算出的挠度最大为4.52 cm，后者大2 cm。

图4 按两版本规范计算的成桥状态挠度比较Fig.4 Comparison of deflection in operation situation between different specifications

图4所示为成桥状态下《2004规范》与《85规范》按预压应力折减0.8后的变形对比，在靠近墩部的挠度基本相同，但跨中挠度相差较大，最大差值为2.61 cm。

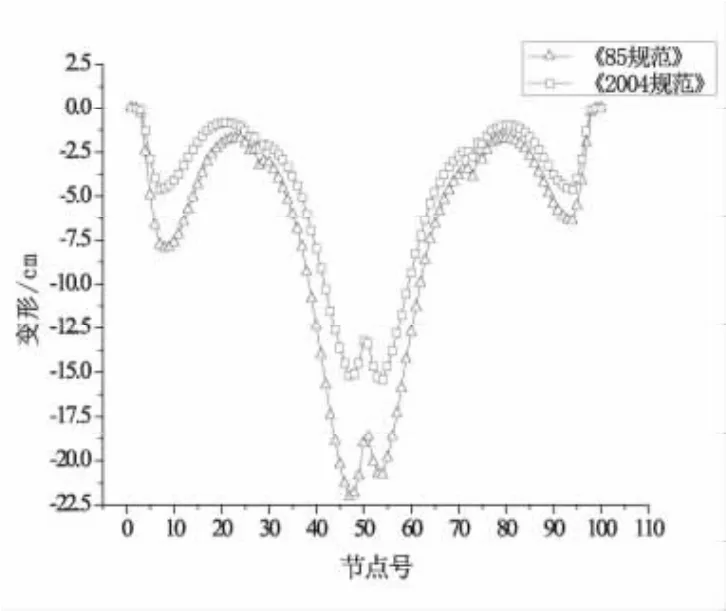
图5 按两版本规范计算的运营10 a后挠度比较Fig.5 Comparison of deflection operated in ten years between different specifications

由图5可以看出，成桥阶段运行10 a后《85规范》计算出的最大挠度(22.0 cm)，比《2004规范》计算出的最大挠度(15.2 cm)大6.8 cm。和成桥时两者差值相比较，随着运营时间的增长，新旧规范设计的桥梁下挠差值增大。

3.3 预拱计算公式不同引起的线形变化

图6 按两版本规范计算的预拱度比较Fig.6 Comparison of camber between different specifications

由图6可以看出，两版本规范得到的预拱度趋势基本相同，但在峰值处《85规范》计算的最大预拱度为17.8 cm;而《2004规范》计算值为23.2 cm，是《85规范》的1.30倍，与0.89 ηθ=1.25基本接近。预拱度增大使得连续刚构桥有更大的下挠空间，运营期挠度较《85规范》小，线形更加合理。

4 结语

笔者针对《公路钢筋混凝土及预应力混凝土桥涵设计规范》2004版和1985版，分析了新旧规范在抗裂验算要求、徐变计算模式、刚度取值和预拱度计算公式等方面的不同对连续刚构桥线形的影响，结合具体工程实例，开展了预应力混凝土连续刚构桥主梁线形分析，得出如下结论:

1)在相同条件下，按《2004规范》设计的刚构桥因徐变引起的下挠值较《85规范》小;

2)按《2004规范》抗裂验算要求计算出的大跨度连续刚构桥梁下挠值比按《85规范》偏小;

3)由于《2004规范》引入了长期增长系数ηθ，按此计算的预拱度值约为《85规范》的0.89 ηθ倍，使得运营期间桥梁线形更趋美观、合理。

［1］鄢余文，杨云蓉.公路桥梁新旧规范计算简支空心板梁比较分析［J］.结构工程师，2006，22(3):20－22.

［2］朱宇峰，王解军.大跨径连续刚构桥施工控制中的混凝土徐变分析［J］.公路工程，2008，33(1):32 －35.

［3］李炳秋，颜全胜.大跨径轻轨连续刚构施工控制中的混凝土徐变影响［J］.中国水运，2008，8(10):239 －240.

［4］方贤平，雷波.特大跨径连续刚构新旧规范设计对比［J］.公路，2007(9):70－73.

［5］李振军.采用新、旧规范计算大跨连续刚构桥的差别［J］.黑龙江交通科技，2007(7):70－73.

［6］张永水，曹淑上.连续刚构桥线形控制方法研究［J］.中外公路，2006，26(6):83－86.

［7］余志武，谈遂.预应力混凝土桥梁施工控制结构分析计算方法［J］.铁道科学与工程学报，2006，3(6):7 －13.

［8］饶瑞，王荣辉.珠海横坑大桥悬臂施工桥面线形监控［J］.中外公路，2004，24(5):68 －71.

［9］王国安，孟庆峰.乌江刚构桥悬臂施工中的位移控制［J］.世界桥梁，2007(2):48－50.