一种异步发射信号的MIMO差分检测方法*
(中国西南电子技术研究所,成都610036)
1 引 言
近年来,MIMO技术得到了广泛、深入研究[1-7]。在这些研究中,都假设发射机的各发射天线同时发射信号,并且各发射天线的发射信号同时到达接收机(本文简称为同步MIMO),现阶段的MIMO技术研究也都主要是在同步MIMO基础上进行的。在同步MIMO技术中,V-BLAST(Vertical Bell Laboratories Layered Space-Time)算法[8-12]以其很高的频谱效率得到了广大学者的关注,但是,基于排序干扰抵消的V-BLAST检测算法要求系统的接收天线数目不小于发射天线数目,从而限制了V-BLAST算法在移动终端上的应用。因为移动终端受到体积的限制,无法放置过多的天线,即使可以放置较多的接收天线,也会由于天线间距离太近,信道的相关性变大,严重影响检测性能。另外,V-BLAST算法无法进行非相干检测,必须进行信道估计。
因此,本文首先提出了一种基于异步发射信号的MIMO系统模型,推导出了一种接收信号基带数学模型。同时,针对多天线系统中精确的信道估计比较困难的问题,提出了一种基于异步发射信号的MIMO系统差分检测方法。该方法使得系统无需进行信道估计,频谱效率与V-BLAST相同,并且利用1根接收天线即可进行检测。
2 系统模型
2.1 发射机模型
这里考虑一个发射天线数为M、接收天线数为L的V-BLAST系统,发射机模型如图1所示。
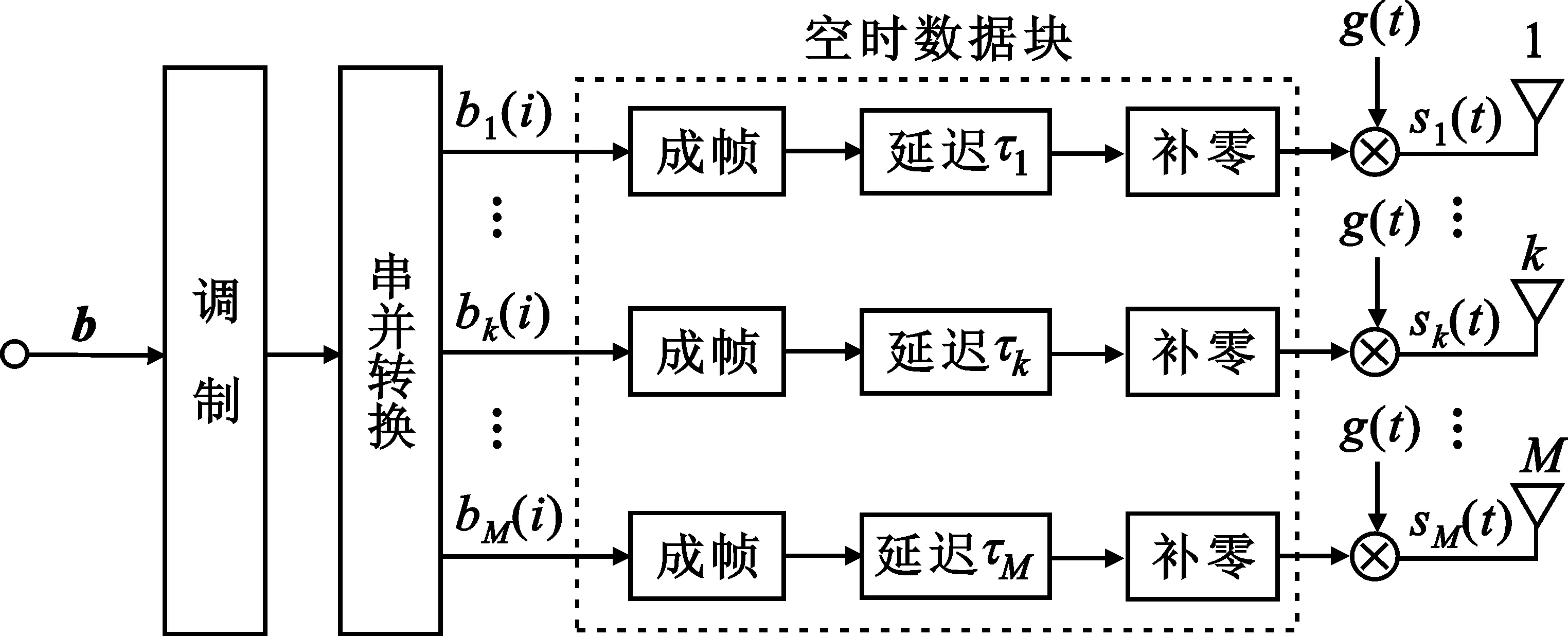
图1 基于异步发射信号的MIMO系统发射机框图
信号矢量b经过调制、串并转换生成M个数据子流,对于这些空间复用的数据子流经过成帧后,人为地添加时间延迟τ1,τ2,…,τM。为了避免块间干扰,在每个数据子流上补零,这M个数据子流形成一个空时数据块。
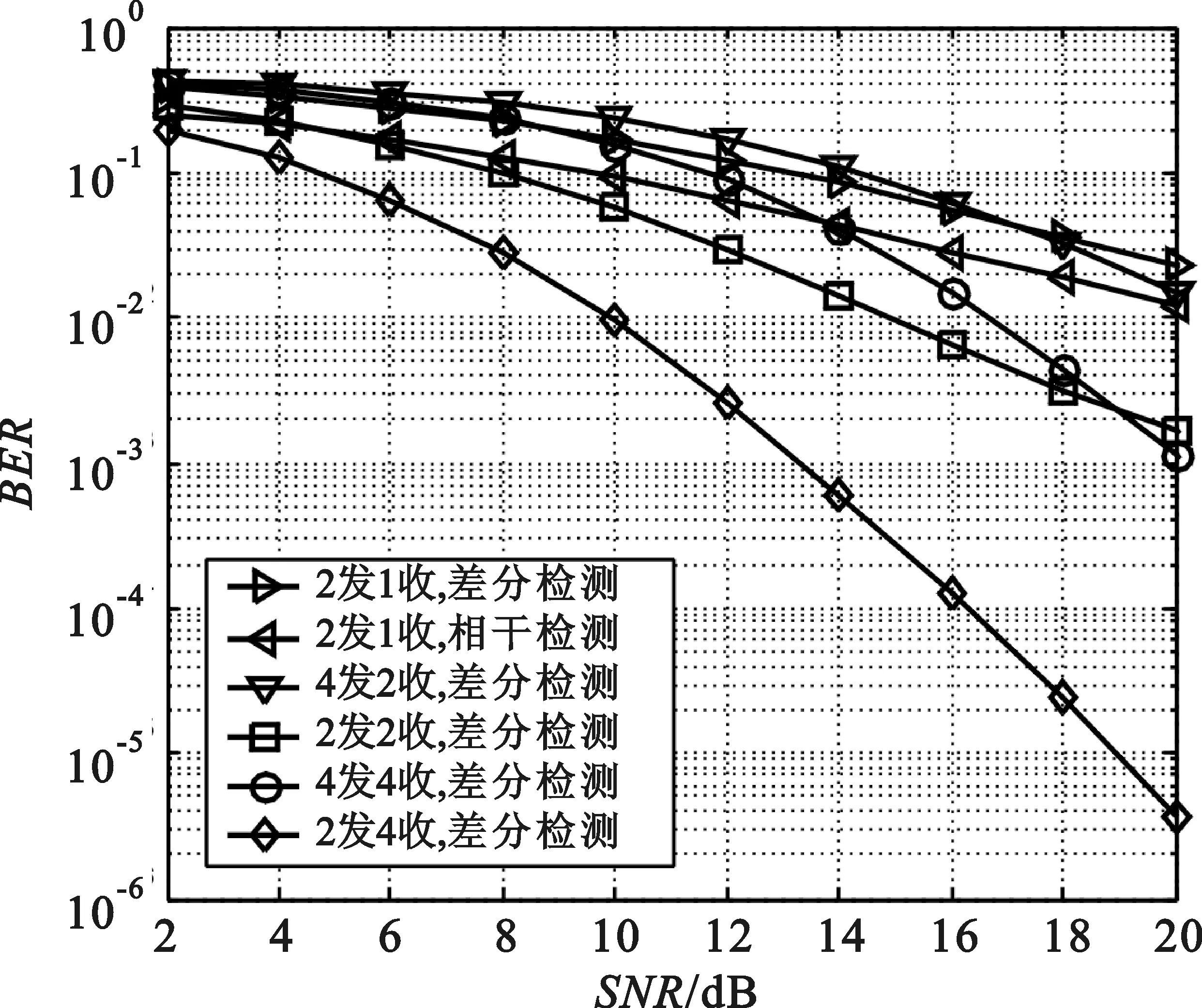
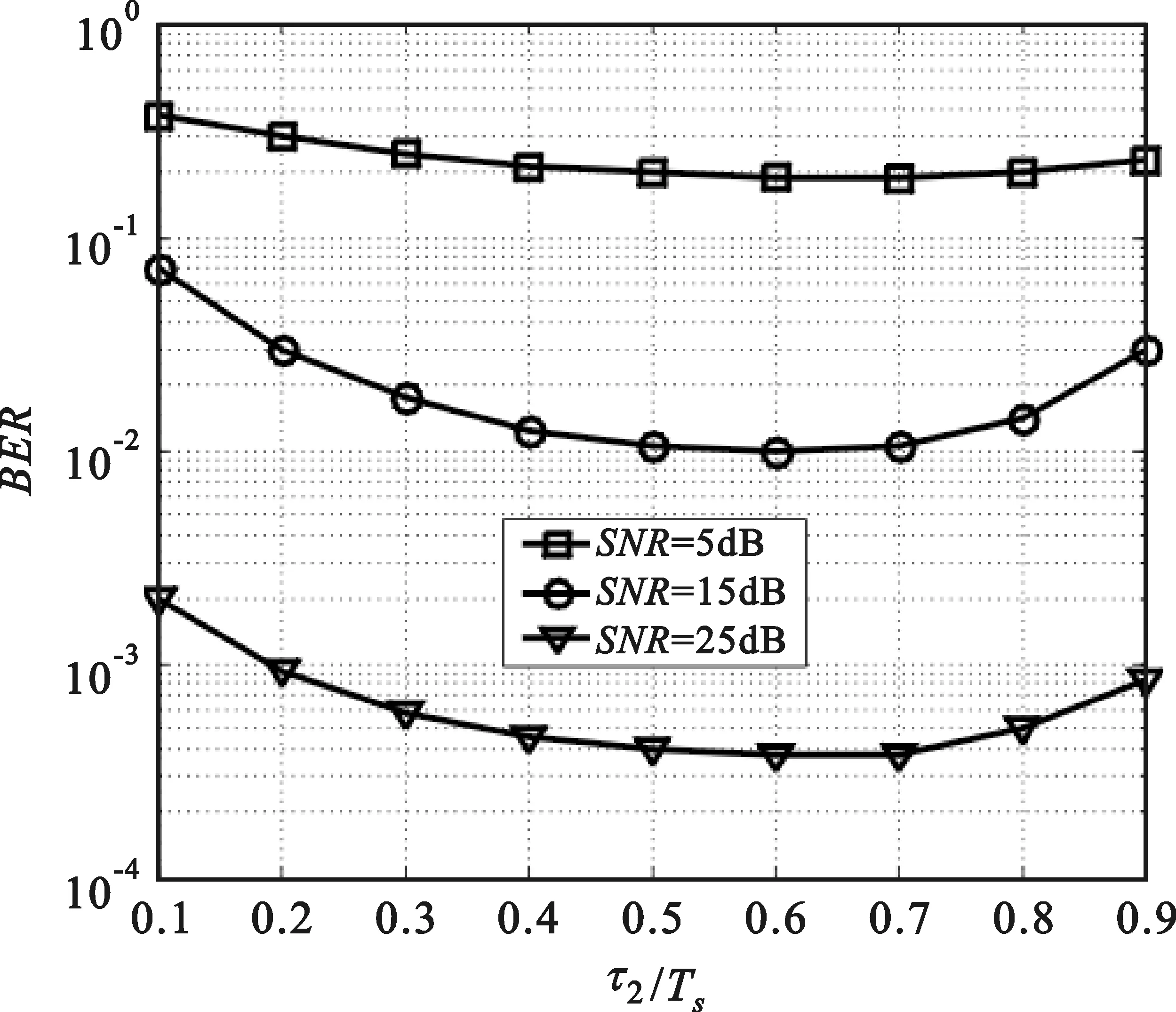
假设每个数据帧内包含N个符号,第k根发射天线的时间延迟为τk,因此,整个空时块包含了N×M个数据符号。不失一般性,这里假设各发射天线的时间延迟满足0=τ1<τ2<…<τM (1) 式中,Es是M根发射天线的总发射功率,这里假设各天线的发射功率相等;bk(i),i=0,1,2,…,N-1是第k根发射天线上在第i个时隙内发射的符号;g(t)是发射天线的等效复基带波形,且满足: 由上可知,由于人为添加了时间延迟,每根发射天线的数据子流信号是异步发射的。 在接收端,第j根接收天线的接收信号可表示为 (2) 图2 基于异步发射信号的MIMO系统接收机框图 一种接收机模型如图2所示,第j根接收天线接收的信号首先进入匹配滤波器组中进行匹配滤波。在第n个时隙对第m根发射天线的匹配滤波输出可表示为 (3) 假设接收端已知发送端的时间延迟τm,将式(1)、式(2)代入式(3)可得: g(t-iTs-τk)g*(t-nT-τm)dt+ (4) 式中,hjk(i)是第i个时隙内,发射天线k到接收天线j间的信道衰落因子。令: g*(t-nTs-τm)dt (5) (6) 因此,式(4)可表示为 ηjm(n) (7) 定义M×M阶互相关矩阵R(n-i),其元素为Rmk(n-i),R(n-i)满足: R(n-i)=R*(i-n) (8) 式中,(·)*代表复共轭转置操作,由g(t)的定义及时延取值范围可知: R(n-i)=0,|n-i|>1 (9) 设第j根接收天线在第n个符号对应时隙的对角信道矩阵为 hj(n)=diag{hj1(n),hj2(n),…,hjM(n)} (10) 第j根接收天线匹配滤波器组在n=0,1,2,…,N-1时刻的输出可表示为向量形式: (11) 式中,yj(n)=(yj1(n),yj2(n),…,yjM(n))T,b(n)=(b1(n),b2(n),…,bM(n))T,ηj(n)=(ηj1(n),ηj2(n),…,ηjM(n))T,(·)T代表矩阵转置操作。为了简化式(11),定义: (12) Hj=diag{hj(0),hj(1),…,hj(N-1)} (13) (14) b=(bT(0),bT(1),…,bT(N-1))T (15) (16) 这样,从符号时隙0~N-1在接收天线j上进行匹配滤波后提取到的信号Yj可表示为 (17) 如式(17)所示,在上述提出的异步发射信号的MIMO系统模型中,信号检测问题可以通过对一个空时数据块的符号进行联合检测。依照式(17),可采用迫零(ZF)、最大似然(ML)等相干检测方法。但是相干检测方法需要接收端已知信道信息,在很多应用场景下,精确的信道估计很困难,采用非相干检测方法是比较好的选择。下面给出一种基于上述异步发射信号的MIMO系统差分编码及检测方法。 在差分方式下,由于接收端未知信道信息,数据在发送之前需要进行差分编码。开始前,发送端发射一个初始矩阵X0进行初始化: (18) (19) (20) (21) 矩阵Xl按行分成M个数据子流,每个数据子流按照图1中的成帧、延时、补零、调制后发射出去。 第l个空时数据块发射后经过无线衰落信道,在第j根接收天线处的接收信号经过匹配滤波之后,由式(17)可得: (22) 式中,上标“l”代表第l个空时数据块对应的接收量。为简化起见,首先假设有1根接收天线,上式可简化为 (23) 这里假设延时参数τ1,τ2,…,τM是固定的,并且接收端已知该参数(系统同步过程中可获得),所以,矩阵R是已知的。将式(23)两端同时乘以R-1,可得: (24) bl=Wlbl-1 (25) (26) (27) (28) (29) 本节仿真验证了2根发射天线和4根发射天线系统的性能;在2发1收情况下将差分检测与相干检测方法的性能进行了对比;验证了在不同时间延迟情况下系统误码率是不同的。仿真中,设定N=2,BPSK调制方式,信道为归一化的平坦瑞利衰落信道。 图3给出了2根发射天线和4根发射天线系统的性能。仿真中,2根发射天线情况下,τ1=0,τ2=0.6Ts;4根发射天线情况下,τ1=0,τ2=0.3Ts,τ3=0.6Ts,τ4=0.9Ts。图3也给出了在2根发射天线情况下,差分检测方法与相干检测方法的性能对比曲线。图3表明,该差分检测方法利用1根接收天线即可进行差分检测;与相干检测方法对比,差分检测方法在性能上有3 dB的性能损失,但是,差分检测方法无需接收端已知信道信息,因此,系统无需进行信道估计,提高了系统效率。 图3 2发射天线、4发射天线系统差分检测性能 图4给出了在2发2收情况下,系统误码率性能随时间延迟的变化特性。结果表明,在相同信噪比条件下,不同时间延迟对应的系统误码率性能不同,在时延从0~0.9Ts变化过程中,误码率先降后升,在2根发射天线的情况下,时间延迟为0.6Ts左右时性能最优。这一结果说明,可以人为调整时间延迟,使得系统获得更好的性能。 图4 2发2收情况下,误码率性能与相对时间延迟变化的关系 本文研究了一种基于异步发射信号的MIMO系统,提出了一种基于异步发射信号的MIMO差分检测算法,解决了传统V-BLAST方法无法进行差分检测的难题,并且利用1根接收天线即可进行检测。仿真结果表明,基于异步发射信号的MIMO系统差分检测方法的性能随相对时延的变化而变化,存在一个相对时延参数使得系统获得最佳的性能,例如,在2根发射天线的情况下,相对时延为0.6Ts左右时性能最优,该结论为基于异步发射信号MIMO系统的最优时延参数选取提供了依据。 参考文献: [1] Foschini G J. Layered space-time architecture for wireless communication in a fading environment when using multi-element antennas[J].Bell Labs Technical Journal, 1996, 1(2): 41-59. [2] Foschini G J. On the limits of wireless communication in a fading environment when using multiple antennas[J].Wireless Personal Communications, 1998, 6(3): 311-355. [3] Raleigh G G, Cioffi J M. Spatio-temporal coding for wireless communication[J]. IEEE Transactions on Wireless Communications, 1998, 46(3): 357-366. [4] Xu Zhu, Ross D M. Performance Analysis of Maximum Likelihood Detection in a MIMO Antenna System[J]. IEEE Transactions on Wireless Communications, 2002,50(2):187-191. [5] Catreux S,Erceg V,Gesbert D,et al.Adaptive modulation and MIMO coding for broadband wireless data networking [J]. IEEE Communications Magazine,2002,39(6):108-115. [6] Gesbert D, Shafi M, Da-shan Shiu, et al. From theory to practice: an overview of MIMO space-time coded wireless systems[J]. IEEE Journal on Selected Areas in Communications, 2003, 21(3): 281-302. [7] Paulraj A J, Gore D A, Nabar R U, et al. An overview of MIMO communications-A key to gigabit wireless[J]. Proceedings of the IEEE, 2004, 92(2): 198-218. [8] Golden G D, Foschini G J, Valenzuela R A,et al. Detection algorithm and initial laboratory results using V-BLAST space-time communication architecture[J]. Electronic Letters,1999,35(1):14-16. [9] Narasimhan R. Error propagation analysis of V-BLAST with channel-estimation errors[J]. IEEE Transactions on Communications, 2005, 53(1): 27-31. [10] Rontogiannis A A, Kekatos V, Berberidis K. A square-root adaptive V-BLAST algorithm for fast time-varying MIMO channels[J]. IEEE Signal Processing Letters, 2006, 13(5): 265-268. [11] Li J, Cao F F, Yang J. Low-complexity algorithm for near-optimum detection of V-BLAST systems[J]. IEEE Signal Processing Letters, 2007, 14(9): 593-596. [12] Francois G, Sergey L. On outage and error rate analysis of the ordered V-BLAST[J]. IEEE Transactions on Wireless Communications,2008,7(10):3679-3685.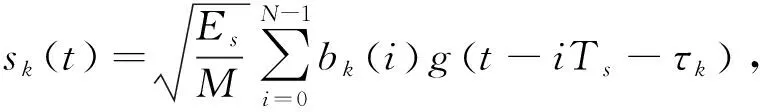

2.2 接收机模型
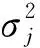
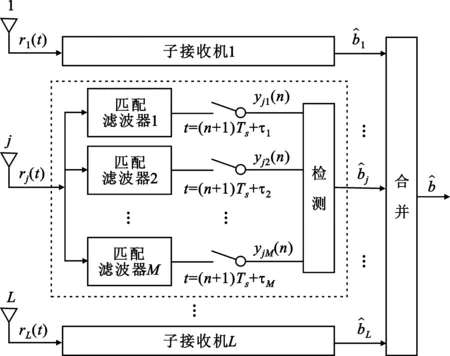
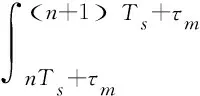
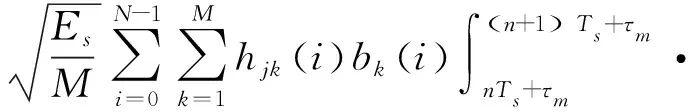
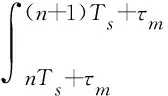
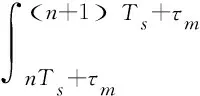
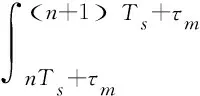

3 基于异步发射信号的MIMO差分编码及检测
3.1 差分编码
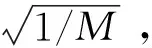
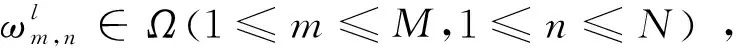
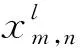
3.2 差分检测
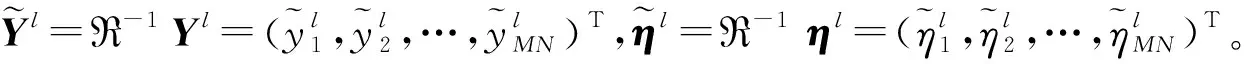
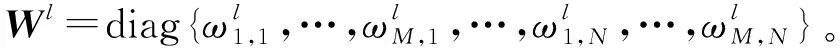
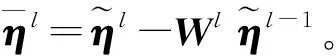
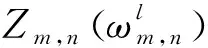
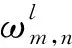
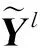
4 仿真结果及分析
5 结 论

