多级维纳滤波测向算法的参考信号优化方法

李 堰,2，宋爱民，刘 剑

(1.空军工程大学 电讯工程学院，西安 710077；2.解放军95482部队，成都 610081)

1 引 言

测向(Direction-finding)作为阵列信号处理的一个重要的研究方向，广泛应用于雷达、通信、声纳、地震、射电天文以及生物医学工程等众多军事和国民经济领域[1-2]。传统MUSIC算法测向需求样本协方差矩阵并进行特征分解，运算量约为O(m2n+m3)，其中m是阵列的阵元个数，n是采样快拍数。如果增加阵元数，运算量会急剧增加。为降低运算量，将多级维纳滤波(MSWF)[3-6]引入到MUSIC算法中，利用它的正交分解特性来快速估计噪声子空间。

在MSWF技术中，其参考信号的取值对算法很关键，本文对参考信号为第一个阵元接收数据和m个阵元接收数据平均值时的两种常用取值情况进行分析，针对这类以阵元数据为参考信号取值的结构，提出一个以任意多个阵元的数据平均值为取值的参考信号取值公式，并对其进行分析，找出此类参考信号结构的最佳取值，使优化后的算法比其它此类结构取值算法在判断信源数估计值和均方根误差方面有更好的性能。

2 阵列信号模型及参数

参照文献[1,2]中阵列信号模型，建立模型如图1所示。设有p个窄带远场信号si(k)(i=1，2,3,…，p)，天线阵列为m个全向同增益均匀线阵，阵元间距为d=λ/2。k为第k次快拍，λ为信号波长，φi为信号入射角度。

图1 等距线阵与远场信号si(k)Fig.1 Equispaced linear array and far-field signal si(k)

信号矢量为s(k)=[s1(k),s2(k),…,sp(k)]T，噪声矢量为e(k)=[e1(k),e2(k),…,ep(k)]T，相邻两阵元间相位差ωi=2πdsinφi/λ，方向向量为a(ωi)=[e0,e-jωi,…,e-j(m-1)ωi]T，方向矩阵为A(ω)=[a(ω1),a(ω2),…,a(ωp)]。

由以上式子得阵元接收信号为

A(ω)s(k)+e(k)

(1)

3 多级维纳滤波算法

3.1 多级维纳滤波降维的基本原理

Goldstein等人提出了一种有效的降维技术，即多级维纳滤波器(Multistage Wiener Filter,MSWF)技术[3-6]，可以利用MSWF的多级分解特性来实现信号子空间和噪声子空间的快速估计。

图2 D=2时的维纳滤波器正交投影分解Fig.2 Orthogonal projection decomposition of Wiener filter for D=2

3.2 基于多级维纳滤波的MUSIC算法

本文利用多级维纳滤波的D阶分解，利用的子空间[8-9]求出信号来向，其具体步骤如下：

第一步：初始化参考信号d0(k)和阵列接收数据xo(k)；

第二步：求互相关矢量hi(i=1，2，3,…，D)：

(2)

(3)

xi(k)=xi-1(k)-hidi(k)

(4)

第三步：由式(2)求得hi估计子空间H、信号子空间S和噪声子空间G(求G时D=m)：

H=spanh1,h2,…,hD

(5)

S=[h1,h2,h3,…,hp]

(6)

G=[hp+1,hp+2,…,hm]

(7)

第四步：利用谱峰搜索公式求信号来向[1,2]。

P(φ)=1/aH(φ)GGHa(φ)

(8)

式(8)是谱峰搜索的噪声子空间方法。

将GGH=I-SSH[2]代入得：

P(φ)=1/aH(φ)(I-SSH)a(φ)

(9)

式(9)是谱峰搜索的信号子空间方法。式(8)、式(9)解出空间谱函数的极大值对应的φ就是信号来向。由于实际应用中参考信号不可避免的引入噪声，信号矢量不再和噪声矢量正交，匹配滤波器中加入了噪声的特征矢量，而信号特征矢量则泄漏到噪声子空间，因此p级的维纳滤波器不足以表示所有的信号矢量[10]。故在式(6)、式(7)中使用信号源数估计值代替p进行计算。

4 参考信号的优化处理

由于对所获取信号的信息利用程度不同，选择不同的参考信号d0会导致不同的性能，对算法性能影响很大，其取值就显得非常关键。对参考信号取值为第一个阵元接收数据和m个阵元接收数据平均值时的两种常用取值情况进行分析，针对这类以阵元数据为参考信号取值的结构，提出一个以任意多个阵元的数据平均值为取值的参考信号取值公式：

(10)

式中，1≤q≤m。式(2)中q=1时，d0为第一个阵元接收到的数据[8,9,11]；q=m时，d0为m个阵元接收到的数据的平均值[8,12]。

相应地，式(10)中的q行平均也对应于A(ω)前q行数据的平均：

其实部和虚部随着q值的增加在(-1,1)区间来回振荡，从而对算法的性能也产生了影响，验证了仿真图中随着q值变化，算法的RMSE值曲线亦出现振荡变化，即在一定条件下，参考信号公式中q取特定的值能使算法达到最好性能。

在本文仿真条件下，取值公式在q=m-3时的参考信号取值使算法性能最好。

5 仿真及性能分析

信号源数估计值的大小直接影响了多级维纳滤波中信号子空间和噪声子空间的判断[8,11]，故针对多种条件下可能的信号源估计值做均方根误差(Root Mean Square Error,RMSE)性能仿真。

仿真所采用的阵列是各向同性的等距线阵，阵元间距为λ/2，运行次数为1 000次，对信号入射角度为-5°的信号进行角度估计，即φ=-5°。采用不同参考信号的程序进行比较，如式(2)所示，各程序q分别取值为1、2、3、…、m。

5.1 对信号源数估计值性能的比较分析

根据可能的信号源估计值计算出RMSE大小，对多种条件下RMSE性能最佳时的信号源估计值进行仿真。

如图3所示，图3(a)给出了信号源数估计值与信噪比的关系，其中阵元数为6，快拍数为200，信号入射角度为-5°和5°；图3(b)给出了信号源数估计值与快拍数的关系，其中信噪比为10 dB，阵元数为6，信号入射角度为-5°和5°；图3(c)给出了信号源数估计值与阵元数的关系，其中信噪比为10 dB，快拍数为200，信号入射角度为-5°和5°；图3(d)给出了信号源数估计值与角度间隔的关系，其中信噪比为10 dB，阵元数为6，快拍数为200，信号入射角度为-5°和随角度间隔变化的角度。

从仿真中可以看出：图3(a)中拥有不同q值参考信号的程序的信号源数估计值随信噪比增加估计值逐步精确，趋向于预设值2，但随q值的变化，各程序的变化趋势没有规律性；图3(b)中不同q值的信号源数估计值除在q=5时的程序取值为3外，其它q值取值的程序的信号源数估计值均未产生过估计，且所有程序信号源估计值不随快拍数变化而变化；图3(c)中，除在q=5时的程序外，q值取其它值的程序的信号源数估计值随着阵元数的增加，其值也增加为3，产生过估计；图3(d)中随着不同程序随着q值的增加，信号源数估计值越来越多取值为2，过估计程度逐渐减轻。

(a)与信噪比关系

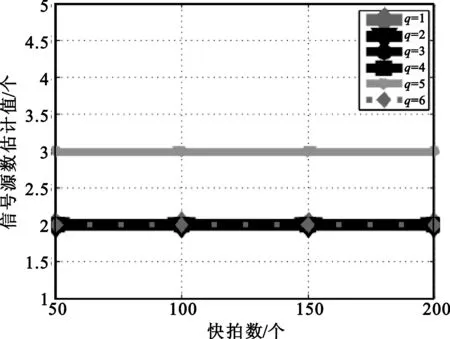
(b)与快拍数关系

(c)与阵元数关系

(d)与信号间隔角度关系图3 信号源数估计值Fig.3 The estimated number of signals

5.2 对均方根误差性能的仿真及分析

采用图3中最佳RMSE性能时的信号源数估计值仿真，从而避免了信号源数估计值的错误估计给均方根误差带来的影响。RMSE定义为

如图4所示，图4(a)给出了均方根误差与信噪比的关系，其中阵元数为6，快拍数为200，信号入射角度为-5°和5°；图4(b)给出了均方根误差与快拍数的关系，其中信噪比为10 dB，阵元数为6，信号入射角度为-5°和5°；图4(c)给出了均方根误差与阵元数的关系，其中信噪比为10 dB，快拍数为200，信号入射角度为-5°和5°；图4(d)给出了均方根误差与角度间隔的关系，其中信噪比为10 dB，阵元数为6，快拍数为200，信号入射角度为-5°和随角度间隔变化的角度。

从仿真中可以看出：随着q值变化，算法的RMSE值曲线在一定范围内来回振荡。图4(a)中除SNR=15的大信噪比外，性能最好的算法其q值均为3，即q=m-3时程序RMSE最小，且各程序RMSE值随信噪比的增加而降低，q=m时的程序性能相对其它程序较差；图4(b)中不论快拍数取何值，性能最好的算法其q值为3，即q=m-3时程序RMSE最小，且除q=m外的各程序RMSE值随快拍数的增加而降低，q=m时的程序RMSE曲线较差；图4(c)中随着阵元数的变化，其性能最好的程序始终为q=m-3，且各程序RMSE值随阵元数的增加而降低，在此图中还可以看出q=m时的程序RMSE性能较差，与图4中其它几个仿真图q=m时的程序性能较差相互证实；图4(d)中RMSE最小的程序并不唯一，图4中由于其它仿真的角度间隔均固定为10°，而图4(d)中10°仿真的结果为q=m-3时RMSE最小，验证了该情况下被优化参考信号的性能最佳，从中还可以看出，随着信号间隔角度增加，除q=m外的各程序RMSE值比较稳定，因为仿真所观测的信号角度并没有发生变化，且q=m时的程序在信号角度间隔为10°和70°的时候较差，选取其它两个信号角度间隔的时候程序性能较好，这也与图4中其它几个仿真在信号角度间隔为10°时取值较差相互印证。

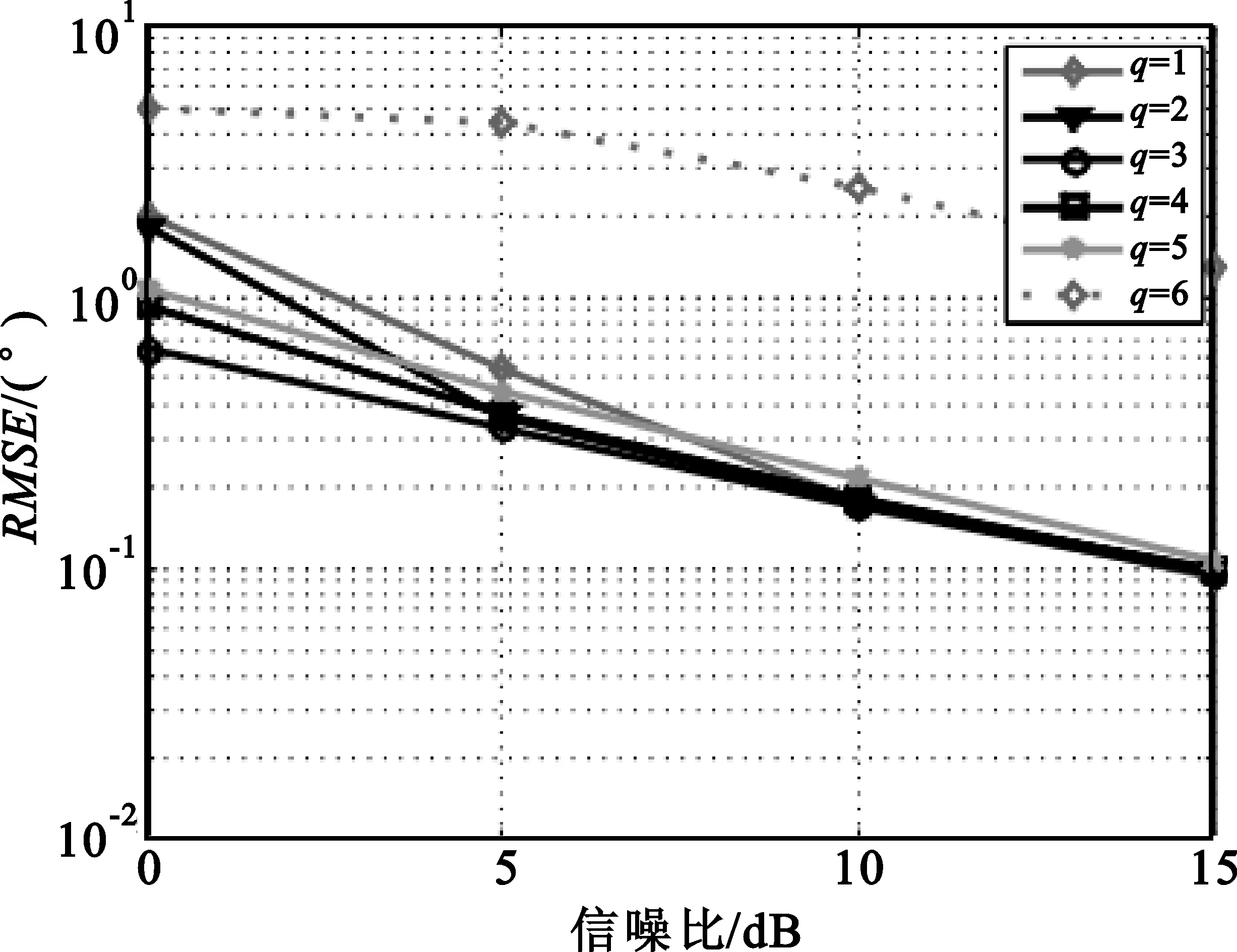
(a)与信噪比关系

(b)与快拍数关系

(c)与阵元数关系

(d)与信号间隔角度关系图4 均方根误差Fig.4 Root mean square error

6 结 论

本文对多级维纳滤波测向算法的参考信号取值进行了分析和研究，根据其结构提出参考信号取值公式，在本文仿真条件下按公式取得最佳参考信号取值，使得算法达到最好的性能，对于提高测向算法的精度具有重要意义。通过对不同取值引起的不同算法性能进行了仿真比较，证明了该方法的可行性。

从理论上对参考信号进行分析，发现方向矩阵的取值对本文参考信号的取值有很大影响，使得在一定条件下，参考信号按本文的公式取特定的值能使算法达到最好性能。本文的下一步工作是着手研究参考信号的取值与最佳算法性能的规律性，从理论上推导出它们之间的关系。

参考文献：

[1] 王永良，陈辉，彭应宁，等．空间谱估计理论与算法[M]．北京：清华大学出版社，2004.

WANG Yong-liang, CHEN Hui, PENG Ying-ning, et al. Spatial Spectrum Estimation Theory and Arithmetic [M]. Beijing: Tsinghua University Press, 2004. (in Chinese)

[2] 张贤达．现代信号处理[M]．北京：清华大学出版社，2002.

ZHANG Xian-da. Modem Signal Processing [M]. Beijing: Tsinghua University Press, 2002. (in Chinese)

[3] Goldstein J S,Reed I S. A new method of wiener filtering and its application o interference mitigation for communications [C]// Proceedings of the 1997 MILCOM. Washington D C: IEEE, 1997:1087-1091.

[4] Goldstein J S, Reed I S,Scharf L L. A multistage representation of the wiener filter based on orthogonal projections [J]. IEEE Transactions on Information Theory, 1998, 44(7): 2943-2959.

[5] Witzgall H E,Goldstein J S. Detection performance of the reduced-rank linear predictor ROCKET [J]. IEEE Transactions on Signal Processing, 2003, 51(7): 1731-1738.

[6] Witzgall H E, Goldstein J S. Rock MUSIC-non-unitary spectral estimation [R]. Santiago: SAIC, 2000.

[7] 于红旗，刘剑，黄知涛，等．基于多级维纳滤波的MUSIC方法[J]．信号处理，2007，23(6)：937-940．

YU Hong-qi, LIU Jian, HUANG Zhi-tao, et al. A MUSIC algorithm based on multi-stage wiener filter[J]. Signal Processing, 2007, 23(6): 937-940. (in Chinese)

[8] 黄磊．快速子空间估计方法研究及其在阵列信号处理中的应用[D]．西安：西安电子科技大学，2005．

HUANG Lei. Study on fast subspace estimation method and its applications to array signal processing[D]. Xi′an: Xidian University, 2005. (in Chinese)

[9] 吴建新，王彤，索志勇．一种快速波达方向估计算法[D]．西安：西安电子科技大学，2009．

WU Jian-xin, WANG Tong, SUO Zhi-yong. Fast DOA estimation algorithm based on the multistage wiener filter[D]. Xi′an: Xidian University, 2009. (in Chinese)

[10] Zoltowski M D, Joham M, Chowdhury S. Recent advances in reduced-Rank adaptive filtering with application to high-speed wireless communications [C]//Proceedings of the 2001 SPIE. Wuhan: IEEE, 2001. 1-15.

[11] 包志强．快速稳健的参数估计及波束形成技术研究[D].西安：西安电子科技大学，2006.

BAO Zhi-qiang. Research of Fast and Robust Estimation of Signal Parameter and Beamforming[D]. Xi′an: Xidian University, 2006. (in Chinese)

[12] 石宇．阵列信号处理中信号参数估计的研究[D].吉林：吉林大学，2008.

SHI Yu. Sources Parameters Estimation Based on Array Signal Processing [D]. Jilin:Jilin University,2008.(in Chinese)