数字信道中误码发生器的设计与实现

何源洁,李宏利

(中国电子科技集团公司第五十四研究所,河北石家庄050081)

0 引言

随着通信事业的发展,通信系统的测试正在变得越来越重要。为了如实测试通信系统的数字信道性能,常常需要加入一定的具有特定统计特性的随机误码。而信号随机误码插入一般是具有高斯分布特性误码的插入,是数字信道测试设计中的难点。

将线性同余法和Box-Muller变换应用在数字信道测试中使用的高斯误码发生器设计中,采用现场可编程门阵列(FPGA)全数字硬件架构,具有精度高、硬件实现容易、节约硬件逻辑资源和误码率可控的优点,可广泛应用于高速无线和有线通信测试中。

1 算法与方案

1.1 误码发生器的实现结构

随机误码发生器所要求的技术指标为:插入具有高斯白噪声条件下的误比特特性,误比特率为0或1×10-2～1×10-7可调,每量级上步进均为1.0。对于数字信道中误码的插入,实质上是要解决误码分布的产生及误码数量的控制问题。随机误码发生器的过程如图1所示。

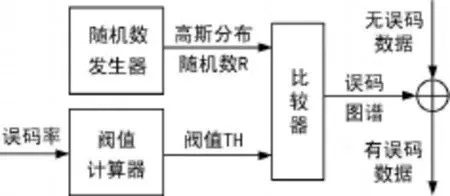
图1 随机误码发生器原理

误码发生器的工作原理如下:首先,根据误码分布特性,随机数发生器产生与随机误码分布特性相一致的随机数序列,同时借鉴真实数字信道中误码数量与判决电平选取相关,误码数量的控制是通过设置与误比特率和误码分布相关的阈值TH来实现。接着,比较器将阈值TH和随机数发生器产生的随机数R相比较,若R≥TH则输出误码标记1,否则输出0,这样就产生了0和1误码图谱数据流。显然误码图谱数据流中的误码标记1的分布与误码分布一致,且其个数与误码数量一致。将具有误码分布特性和数量特性误码图谱数据流与输入的无误码的数据作模二加运算,即完成随机误码的插入。

技术指标要求所设计的随机误码发生器能够模拟高斯白噪声信道下的误码特性,因此,随机数发生器产生的随机数必须服从高斯分布。得到高斯分布随机数的关键是:首先得到均匀分布的随机数,然后通过变换得到高斯分布的随机数。

1.2 均匀分布随机数的产生

均匀分布随机数是产生其它分布随机数的基础,如高斯分布和指数分布等,因此产生均匀分布随机数的好坏直接影响到所产生的高斯随机数的性能。所以均匀随机数的产生至关重要。

常用的均匀随机数的产生方法主要有线性同余法、反馈位移寄存法和组合同余法。其中线性同余法实现简单、占用存储单元少,是目前应用最广泛的方法之一。

线性同余法是由莱默(Lehmer)于1951年提出来的,此方法是利用数论中的同余运算来产生随机数,故称为同余发生器。其递推公式为:

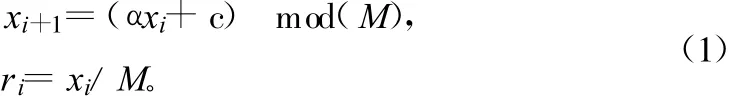
式中,α为乘子(常数);c为增量(常数);x0为种子;M为模;α,x0和 M都是正整数;i为迭代次数;ri为(0,1)区间均匀分布的随机数。

1.3 高斯分布随机数的产生

由随机信号理论可知,在(0,1)区间上服从均匀分布的随机数经过一定的变换,可产生服从N(0,1)的高斯随机数。该变换就是Box-Muller变换法。Box-Muller变换法产生高斯随机数的计算式为:

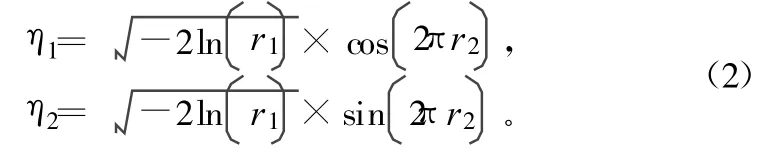
式中,r1和r2为互相独立的(0,1)区间均匀分布随机数。

用式(2)产生高斯分布随机数的精度高,可以同时产生一对互为正交的独立高斯随机数,应用较为广泛。实现时可分别建立正余弦表和自然对数平方根表,将前面生成的均匀分布的随机数作为地址就可以通过查表来实现Box-Muller变换。

2 硬件实现

2.1 硬件组成

数字信道中高斯随机误码产生器的实现框图如图2所示,其中监控计算机作为主控制器和误码门限值的计算。监控计算机与FPGA之间通过串口进行门限的设置。FPGA作为信号实时处理器,实现信号的输入/输出以及随机误码的实时插入。

图2 高斯随机误码发生器实现

该设计中采用Altera公司Cyclone系列FPGAEP1C12芯片来完成误码发生器的工程实现。Cyclone系列是Altera公司于2003年推出的具有高性价比的FPGA系列产品,EP1C12芯片可用的资源包括:12 060个逻辑单元、234 kbit的RAM和2个锁相环。该系列芯片使用灵活、功能丰富、成本低、便于开发。这种方案的优点是:采用计算机作为主控制器可以实现多种人机交互接口;采用FPGA作为实时信号处理器可以利用其强大的实时信号处理能力完成高速的数据流的误码实时插入,且FPGA具有多次可编程的优点使得系统的扩展和升级变得非常容易。此外利用串口配置阈值或将阀值存储到FPGA的存储器中,使得阈值的处理非常方便;同时利用FPGA产生随机数,不需要额外的存储空间节约了成本,降低了设计难度。

2.2 处理流程和难点

高斯随机误码插入的流程是外部输入没有误码的数据和时钟,用输入时钟推动均匀随机数发生器按式(1)描述的算法用VHDL语言实现,输出2组不同的(0,1)区间均匀分布的16 bit位宽的无符号随机数。然后使用查表法实现Box-Muller变换,得到高斯分布的随机数。由于误比特率为0或1×10-2～1×10-7可调,所以对高斯分布的随机数进行了32 bit位宽的量化。

2.3 阀值的计算

根据设置的误比特率Pe和误码分布的概率密度函数(即高斯分布),可以通过式(3)求出阈值TH。

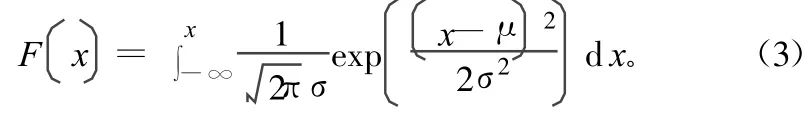
根据要求利用MATLAB可以比较容易得到误码率和门限阀值之间的关系,如表1所示。

表1 误码率与阀值关系表

2.4 硬件仿真

用VHDL语言实现的高斯随机数发生器之后,再用ModelSim软件对其进行硬件仿真,其仿真结果如图3所示。

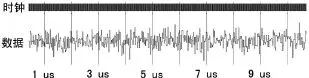
图3 高斯随机数发生器的ModelSim仿真结果

通过对该仿真输出的数据进行高斯分布随机数的直方图和概率校验图的分析,并与MATLAB软件仿真的结果进行了比较,结果表明该VHDL语言实现的高斯随机数发生器完全满足要求。

3 测试结果

根据图2的实现框图,将误码仪的输出数据接到无误码数据流端,再将经过随机误码发生器插入误比特后有误码数据流输出到误码仪,用监控计算机的软件控制插入误码率的门限,随机误码发生器输出端就得到相应的插入误码后的数据流。

所研制的随机误码产生器利用FIREBERD 6000A误码仪进行了测试,测试结果如表2所示。测试结果表明设计的随机误码产生器具有较高的准确性,能够满足数字信道中误码测试的要求。

表2 测试结果对比表

4 结束语

通过对一种高斯随机误码发生器实现方法的介绍,并对其实现的技术难点进行了详细描述。技术难点有3点:①均匀分布随机数的产生;②自然对数平方根表的生成;③误码率阀值门限的计算。

与已有的误码产生方法相比,该方法具有以下优点:误码分布具有足够的随机性,即所产生的误码分布符合高斯随机分布的统计特性;该方法实现电路简单,并采用较小容量的FPGA和相应的接口芯片就实现了高斯误码图案插入。

[1]DANGER J L,GHAZEL A,BOUTILLON E,et al.Efficient FPGA Implementation ofGaussian NoiseGeneratorfor Communication ChannelEmulation[J].The7th IEEE International Conference on Electronics,Circuits and Systems,2000(1):366-369.

[2]张胡平,姚远程,冯 立.高斯分布误码插入的设计和实现[J].无线通信,2008(1):4-6.

[3]刘 江,汪 涛,刘洛琨.基于FPGA实时可配置的高斯白噪声发生器[J].现代电子技术,2005(6):13-15.