以平行四边形为周期的双正交插值周期尺度函数的构造

刘荣辉，王 芳

(大庆师范学院 数学学院，黑龙江 大庆 163712；2.大庆市宏伟热电厂 教育科，黑龙江 大庆163711)

我们知道，如果尺度函数具有基插值性质，则在实际应用中是非常方便的。因为此时对于给定的尺度，信号在相应尺度子空间上的投影系数恰为信号的均匀取样，从而省去了预处理过程，大大节省了计算量。本文就给出了以平行六边形为周期的双正交插值周期尺度函数的构造。

1 预备知识

n1=e2-(e2,e1)e1,n2=e3-(e3,e2)e2,n3=e1-(e1,e3)e3

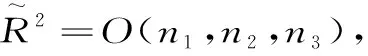
Λ={P|P=(P1,P2,P3)T,P1+P2+P3=0,P1,P2,P3∈Z}

对j≥0，令△j={P|P=(P1,P2,P3)T∈Λ,-2jN≤P1,-P2,-P3<2jN}

取τ1=(2,-1,-1)T，τ2=(-1,2,-1)T，E={τ1,τ2} 令

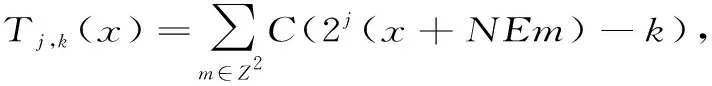
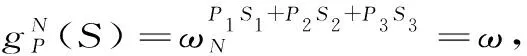
引理1：对j≥0，k∈△j,Γj,k(x)有如下的广义Fourier级数展开形式:

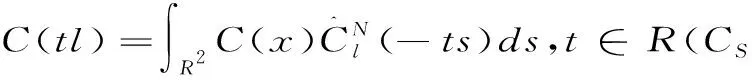
引理2：对∀k∈Λ我们有

我们设初始函数C(x)进一步满足：

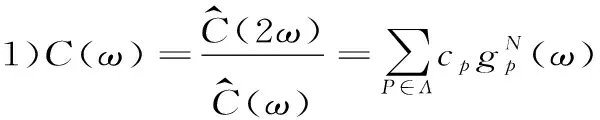
2 正文

命题1：对任意j≥0,,j∈△j函数φj,k(x)的Fourier级数表示为

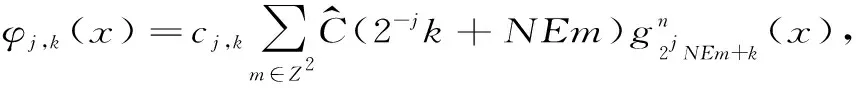
证明： 对任意j≥0,k∈△j，由引理1、2和定义1我们有：

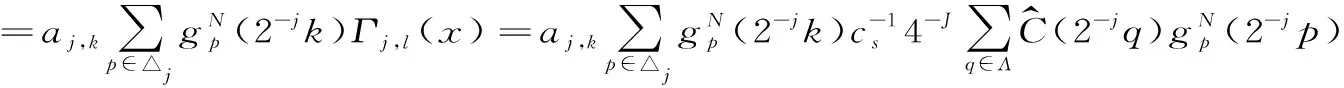
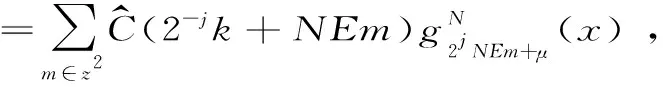
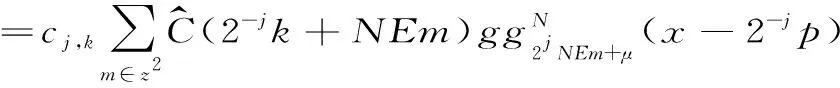
(1)

对任意j≥0，k∈△j，设aj,k=(Ej,φj,k(0))-1,其中Ej=4j3N2，我们定义:

(2)

命题2：对任意意j≥0函数Qj(x)具有插值性质：Qj(x-2-jp)=δp,0对任意的P∈△j。

证明：由上面所述定义式，对于任意j≥0,P∈△j有

(3)

对任意j≥0,k∈△j,定义：Qj,k(x)=Qj(x-2-jk)(3)

则由命题(2)和(1)式可得

命题3：对于任意意j≥0,k,p∈△j由(3)式定义的函数Qj,k(x)具有插值性质：

Qj,k(2-jp)=δk,p

由上面命题，进一步我们有：

证明：为证明{Qj,k(x);k∈△j}构成了Vj的一组基底，我们只需证明它是线性无关的。

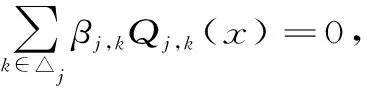
(4)

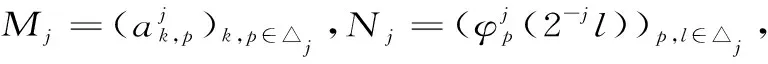
(5)

下面，我们来定义Qj,k(x)(j≥0,k=△j)的对偶函数。

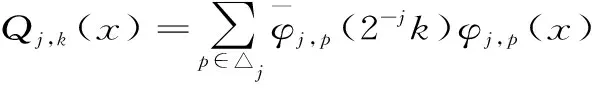
(6)

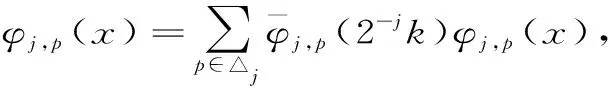
证明：只需证明上式即可。

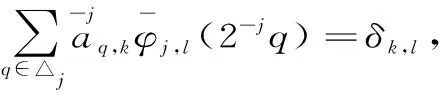
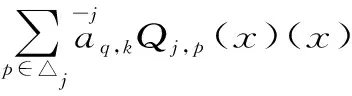
另外，容易得到

命题6：对任意j≥0,k,l∈△j，,设φj,k(x),φj,l(x)分别式由(3)(6)两式定义，则

(φj,k(x),φj,l(x))=δk,l∀k,l∈△j

证明：由定义(3)(6)，对于任意的k,p∈△j，我们有

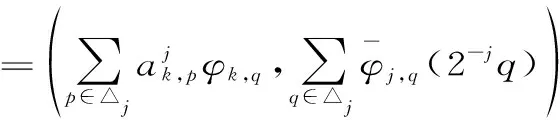
3 结论

命题6说明，对任意j≥0,k,l∈△j,分别由(3)(6)两式定义的Qj,k(x),Qj,l(x)互为对偶函数，我们称其为双正交尺度函数，此函数具有周期性与插值性。由此，我们得到了以平行四边形为周期的具有插值性质的双正交周期尺度函数Qj,k(x),Qj,l(x)。

[参考文献]

[1] 刘荣辉.关于二元Box样条的正交周期小波函数构造[J].大庆师范学院学报,2009,29(3):69-71.

[2] H. L. Chen.Construction of orthonormal wavelets in the periodic case[J].Chinese Science Bulletin,1996,14(7):552-554.

[3] H. L. Chen,D. F. Li.Construction of multidimensional biorthogonal periodic Multiwavelets[J].Chinese Journal of Contemporary Mathematics, 2000, 21(3): 223-232.

[4] C.de Boor and R.Devore, Approximation by smooth multivariate splines[J]. Trans.Amer. Math. Soc., 1993,276:123-166.

[5] C. de Boor, K. H. ollig,S. Riemenschneider.Bivariate cardinal interpolation by splines on a three-direction mesh[J].J.Math.,1985,29:533-566.