非视距误差的TDOA/AOA混合定位算法

李思奇， 陈怀新

（中国西南电子技术研究所，四川 成都 610036）

0 引言

自美国联邦委员会（FCC）公布E-911需求以来，国内外开始出现了研究无线定位技术的热潮。除了 E-911，无线定位在其它领域也大有用武之地，如公路交通的导航、物流的监控、网络优化等。在现有的定位算法中，有接受信号强度（RSS）、到达角（AOA）、到达时间（TOA）、TDOA 等算法，其中TDOA算法不要求基站和移动台之间的同步，而被广泛适用。随着智能天线阵列的适用，基站将能够比较精确的测得AOA值，利用TDOA和AOA相结合的混合定位方法[1-3]，能够得到比单纯使用TDOA方法更好的位置估计。

在无线通信系统中，由于传播环境的影响，引起定位误差的因素除了设备测量参数产生的随机测量误差外，还有电波的多径效应、NLOS传播等影响。其中NLOS误差是影响定位精度的重要因素，NLOS误差的消除是无线定位算法中的关键技术，在一般的定位算法中，如 Fang算法[4]、Chan算法[5-6]、Taylor级数展开法[7]等是假设TDOA噪声服从零均值高斯分布，而现在将其应用于具有较大误差的非高斯环境，必然造成算法性能显著下降，无法取得移动台（MS）的最大似然估计，使得估计位置出现较大偏差。

基于对NLOS误差的分析，通过Wylie鉴别算法识别出具有NLOS误差的基站，然后利用NLOS传播引起附加时延的统计特性估计出附加时延的均值和方差，来重构TDOA值，最后利用基于Taylor级数展开的TDOA和AOA混合定位算法，得出位置估计，有效提高了定位精度。

1 NLOS的鉴别和附加时延估计

1.1 Wylie鉴别算法

在所测得的信号中，因为事先难以确定哪些测量值中包含NLOS造成的误差，所以有必要结合LOS/NLOS鉴别算法，找出包含NLOS误差的信号，常用的算法有Wylie[8]，残差分析鉴别算法[9]等。鉴于残差分析鉴别算法的计算复杂性，这里适用Wylie算法。

第m个基站(BS)在it时，检测的TOA测量值为：

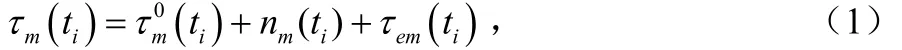
当MS和BS之间存在LOS时，影响TOA测量值的标准测量误差是可以预测的。根据前后两条曲线可以按照式（3）求出拟合时间窗内的标准差可表示为：

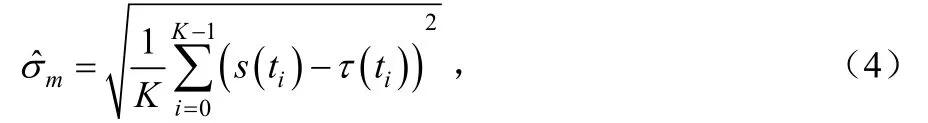
其中，K为测量值样本数。由于NLOS误差与 nm（t）同时存在，并且时间上不相关，因此可以预计 TOA测量值有一个大于平滑值的标准差。

具有NLOS误差基站的辨识准则是：

若假设检验0H 成立，则基站在所检测的时间段内的接收信号为LOS信号；若假设检验1H成立，则基站的接收信号为NLOS信号。

1.2 NLOS附加时延的均值和方差

当存在NLOS误差时，由文献[10]知，在不同信道环境下可以认为服从指数、均匀或Delta分布，认为其服从指数分布，概率密度函数即为：

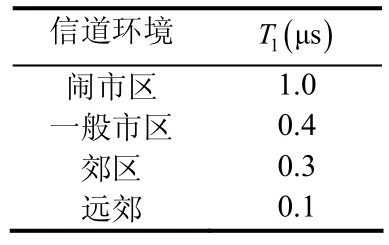
表1 不同信道环境下的 1T参数取值

由τm,rms的表达式知，，因为，所以有，其中，,mrmsτ的概率密度函数为：

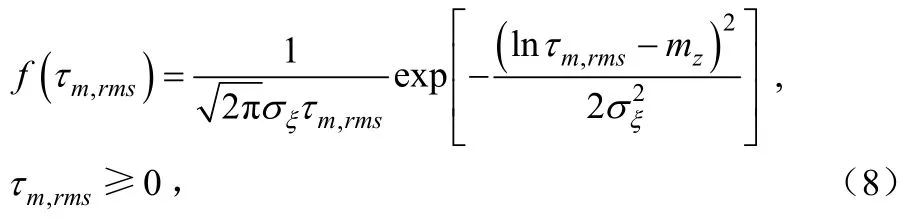
由概率论的知识知，指数分布的随机变量均值和方差分别为：

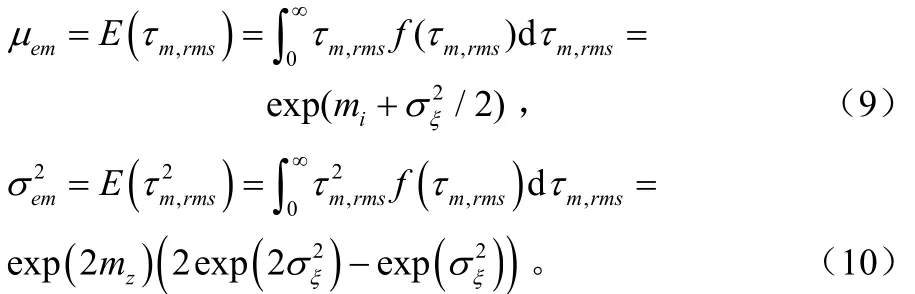
2 TDOA/AOA混合定位算法

2.1 泰勒级数初值的确定

移动台MS的坐标设为(,)xy，参与定位的第m基站BS的坐标为（xm, ym），个数为N，MS到 BS的距离为，设 BS为服务基站（x ,y ），则111相应的距离差为 rm,1=cτm,1=rm-r1,m = 2,3,…N ，τm,1为对应的TDOA时间，c为电波传播速度，可以得到：其中

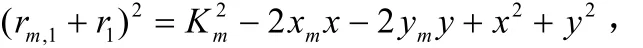
展开并重新组合可得：

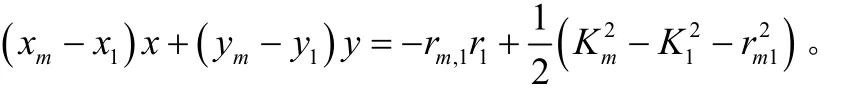
联立方程组，可以得到下面的最小二乘方中间解：

其中

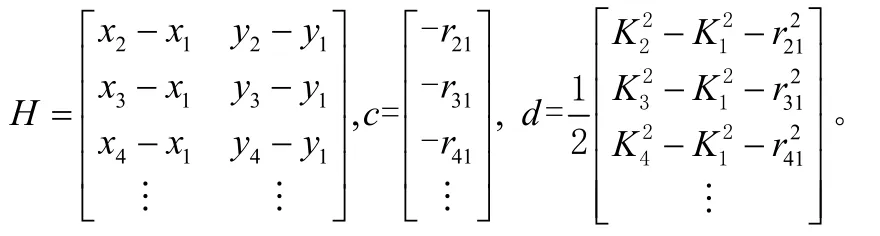
2.2 泰勒级数展开的TDOA/AOA混合定位

第m个BS与MS的距离表示为：

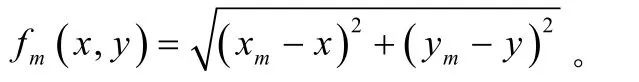
对于一组TOA测量值，该算法首先将上式在选定的MS初始位置（x0, y0）进行泰勒展开，忽略掉二阶以上分量，上式转化为：

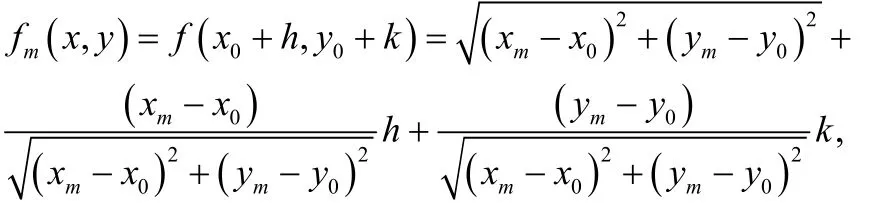
由 rm,1= rm- r1,m = 2 ,3,… N ，将上式化为：

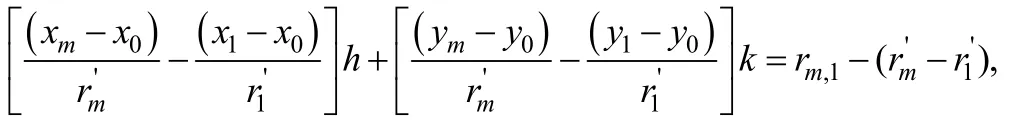
服务基站BS1测得的AOA为α，α服从0均值，标准差为ασ的高斯分布，则：

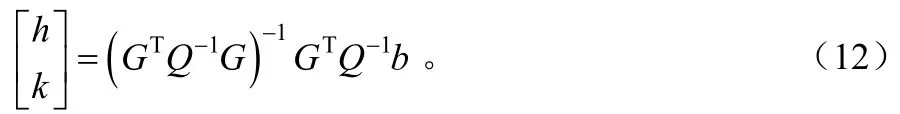
其中Q为TDOA/AOA测量值的协方差矩阵， ,,bGQ 即为如下：

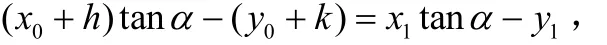
联立方程组，得到加权最小二乘解为：

判断式（13）是否成立。

若成立，停止计算，否则，将：

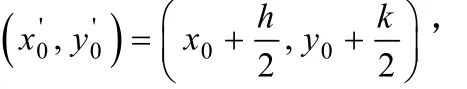
代入式（12）重新计算，直到条件（13）满足，解得的（x0', y0'），即为所求MS的位置估计。

2.3 TDOA值的重构及算法步骤

泰勒级数展开法中，只考虑了系统随机测量误差，当存在NLOS的影响时，定位精度急剧下降。要取得较好的结果及必须对TDOA测量值进行重构以除去NLOS所带来的附加时延误差。算法具体步骤如下：

①由式（5）和式（6），鉴别出哪些 TOA测量值中包含NLOS误差，当存在NLOS时，根据TOA测量值，由式（9）计算附加时延误差μem，重构TOA值

②由式（11），计算出泰勒级数的初始位置估计；

③根据式（10）重构系统测量误差的协方差矩阵，若某个m基站测量值包含NLOS误差，则对应的得到重构后的 Q'；

④根据重构的τm'和Q'，用TDOA/AOA泰勒级数算法计算出MS的位置估计。

3 计算机仿真与结果分析

通过Matlab对所提出的算法进行仿真，并与其它算法进行对比。仿真条件：无线网络小区半径R=2 km，有7个基站参与定位，正六边形分布，服务基站为BS1,并假定服务基站测量值没有NLOS误差,基站坐标为：BS1(0,0),BS2(0,3 646),BS3(3 000,1 732), BS4(3 000,-1 732), BS5(0,-3 454), BS6(-3 000,-1 732), BS7(-3 000,1 732),移动台在小区内均匀分布，如图1所示。TDOA时间测量误差服从高斯分布，均值为0，标准差分别在以下几种情况 0.1µs,0.2µs,0.3µs,0.4µs,0.5µs。

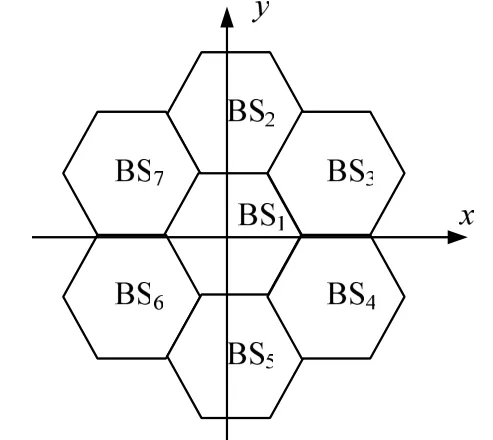
图1 基站的几何分布

图2 所示，当无线网络基站中存在NLOS误差时，比较Chan定位算法（不考虑NLOS鉴别和重构）、基于TDOA的Taylor展开法（采用NLOS鉴别和重构）、提出的NLOS误差TDOA/AOA混合定位法。后两种算法明显优于Chan算法，因为它没有对NLOS误差进行考虑，在一个具有正均值的非高斯噪声中，Chan算法会产生一个较大的偏差。

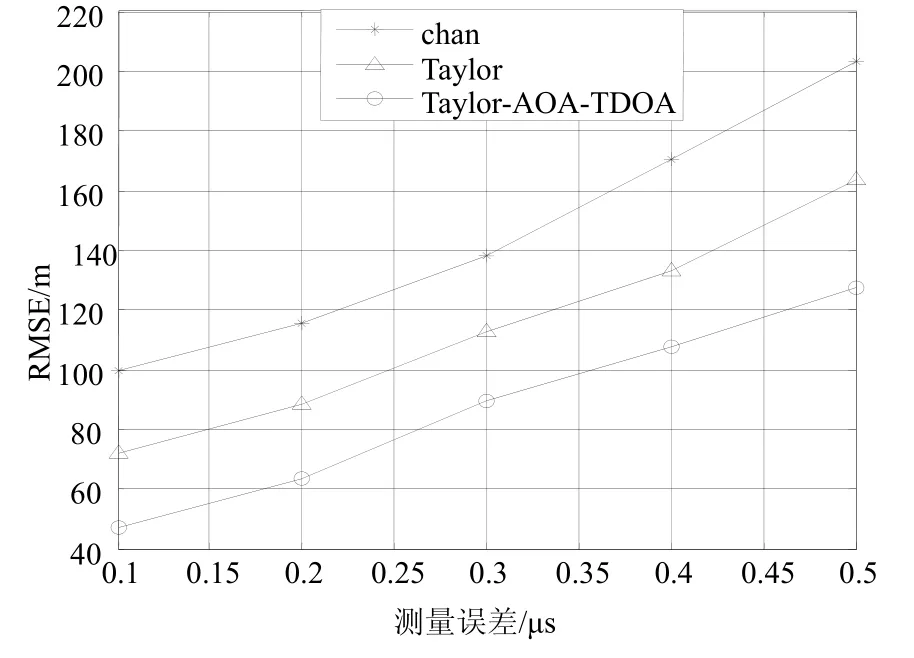
图2 NLOS下的算法性能比较

与TDOA的Taylor展开法相比，提出的NLOS误差的TDOA/AOA混合定位法，有效利用量测值平滑拟合来消除NLOS误差，同时利用AOA的辅助定位信息与TDOA时差信息，减小了目标定位误差，提高了目标定位性能。

图3所示，针对含有NLOS误差的TDOA/AOA混合定位法的性能进行进一步分析。当基站中存在NLOS误差时，比较了当测量角度的标准差在 0.01rad，0.03rad，0.05rad，0.07rad下算法的性能。通过仿真图形可以看出，随着AOA测量标准差的增加，算法精度会下降。

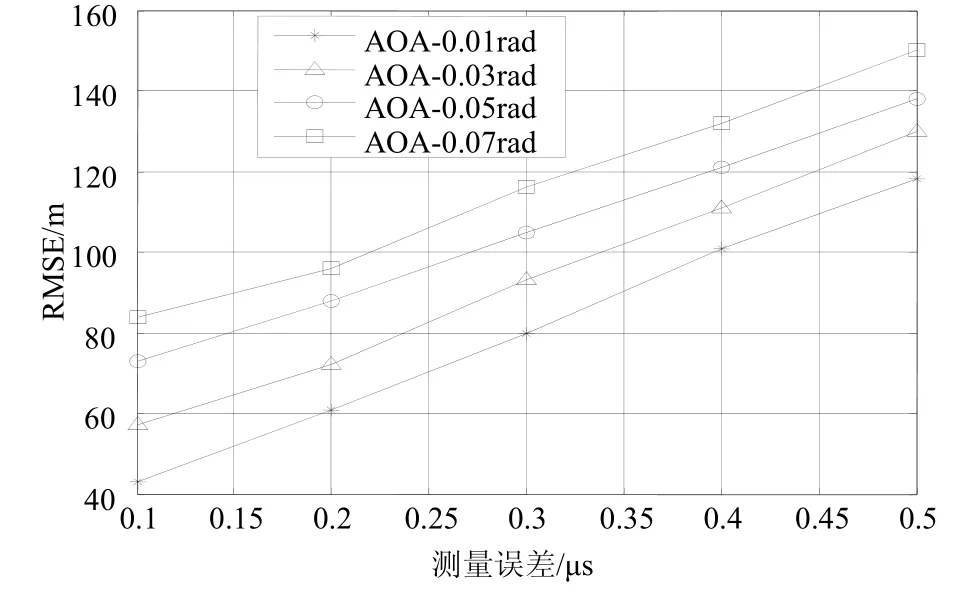
图3 不同AOA测量标准差

4 结语

针对存在NLOS环境下，先通过NLOS误差鉴别算法，鉴别出包含NLOS误差的测量值，然后利用NLOS环境下附加延时的统计特性，重构了测量值，有效的减小了对位置估计的影响，然后利用Taylor级数展开的TDOA/AOA混合定位算法，得出位置估计。仿真结果表明，在测量值中存在NLOS误差的情况下，该算法能有效的提高定位的精度。

[1] CONG L, ZHUANG W H. Hybrid TDOA/AOA Mobile User Location for Wideband CDMA Cellular System[J]. IEEE Tans. On Wireless Communication, 2002, 18(03)： 439-447.

[2] MA CHANGLIN, KLUKAS R, LACHAPELLE G. An Enhanced Two-step Least Squared Approach for TDOA/AOA wireless location[J]. ICC2003,2005(02)： 987-991.

[3] 邓平,李莉,范平志.一种TDOA/AOA混合定位算法及其性能分析[J].电波科学学报,2002,17(06)： 633-636.

[4] FANG B T. Simple Solutions for Hyperbolic and Related Position Fixes[J]. IEEE Trans. On Aerospace and Electronic Systems,1990, 26(05)：748-753.

[5] CHAN Y T, HO K C. A. Simple and Efficient Estimator for Hyperbolic Location[J]. IEEE Trans. On Signal Processing,1994, 42(08)： 1905-1915.

[6] 丁宏毅,柳其许,王巍. Chan定位算法与TDOA估计精度的关系[J].通信技术, 2009,17(06)：75-80.

[7] FOY W H. Position Location Solution by Taylor-Series Estimation[J]. IEEE Trans. On Aerospace and Electronic Systems, 1976,12(02)： 187-193.

[8] WYLIE M P, HOLTZMAN J. The Non-line of Sight Problem in Mobile Location Estimation[C]. USA：IEEE, 1996： 827-831.

[9] CHEN Pi chun. A Non-line-of-sight Error Mitigation Algorithm in Location Estimation[J]. IEEE Wireless Communication and Network,1999(24)：316-320.

[10] GREENSTEIN L J. A New Path-gain/delay Spread Propagation Model for Digital Cellular Channel[J]. IEEE Trans. on VT,1997,46(02)： 177-484.