工业企业节能潜力预测模型研究

王晓杰 周英男 刘环环

(大连理工大学管理学院，辽宁 大连 116023)

工业企业节能潜力预测模型研究

王晓杰 周英男 刘环环

(大连理工大学管理学院，辽宁 大连 116023)

对未来工业企业的节能潜力进行科学的预测是制定工业企业节能政策法律的重要依据，也是指导工业企业进行节能管理的重要组成部分。本文基于灰色系统理论在传统的单变量预测模型基础上，提出了多变量的工业企业节能潜力预测模型，并通过对时间序列的改进，将节能政策的影响考虑到了预测当中，同时以行业内先进企业的用能水平为标杆，完善了预测结果，提高了预测模型的精确度。

工业企业;节能潜力;MGM(1，n)模型

节能潜力是指存在于用能体系的节能数量，通常表示为煤或石油的消费量，如t标煤、t标油。只有明确节能潜力才能制订有效的节能规划，最终实现节能目标。

节能潜力分为理论节能潜力和现实节能潜力。理论节能潜力的计算依据是热力学定律，现实节能潜力则侧重考虑技术、经济诸多因素的影响，常采用因素对比分析法［1］，即通过用能体系内各种能耗因素与相应对比基准比较求得差异，从而得出节能潜力大小。本文所研究的节能潜力为现实节能潜力。

1 现有预测模型

现有企业节能潜力预测模型为单变量灰色预测模型GM(1，1)模型。该模型以单位产品能耗为原始序列建模，预测未来每一年度的单位产品能耗，减去上一年度的单位产品能耗后再乘以年计划产量即可得到预测年份的节能潜力［2］。

实际用能系统中包含了多个变量，每个变量之间相互影响，仅仅用单一变量对其进行分析和预测，精确度难以达到理想标准。基于此，本文引入了多变量的MGM(1，n)模型作为模型构建的基础。

2 模型的构建

2.1 基础模型

多变量的MGM(1，n)模型通过反映系统中多个变量的相互影响与共同发展，从而弥补现有模型的不足。它是GM(1，1)模型在n元多变量情况下的推广，但不是GM (1，1)模型的简单组合，也不同于GM(1，n)模型只建立单个n元一阶微分方程，而是建立n个n元微分方程，通过联立求解，使多变量灰色预测模型中的参数能够反映变量间的相互影响。当n=1时，模型退化为GM(1，1)模型。当B=0时，MGM(1，n)变成n个GM(1，1)模型的组合［3］。

令xi(0)(k)为灰时间序列，xi(1)(k)为相应的一次累加生成序列(i=1，2)，即

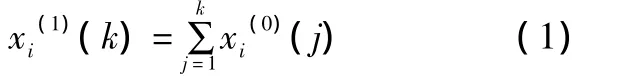
式中k=1，2，…，m。

记x(1)(k)=(x1(1)(k)，x2

(1)(k)，…，xn

(1)(k))T

该模型自提出以后，应用范围比较广，先后应用于机械检测、建筑工程、经济投资等领域，并取得了很好的预测效果。本文考虑了用能系统的特点，将该模型引入到工业企业节能潜力的预测当中，并在以往节能潜力预测变量的基础上选择单位产品能耗和产品产量作为模型的预测变量。

由经济学中的边际分析可知，每多生产一件产品所引起能源投入的增加量呈现递增趋势，但是只要产量在一定的范围内，平均每件产品的能源消耗量会一直处于递减状态，超过某个临界产量时(如图1中的Q*)单位产品所消耗的能源数量将呈现递增状态。因此，可以说单位产品能耗受到产品产量的影响。另外，企业的产品产量取决于市场需求，而在一定的市场需求水平内，对于某一具体企业来说，单位产品能耗降低该企业就会增加产品产量，反之则会减少产品产量，即在一定程度上产量受到单位产品能耗的影响。所以，本文在已有的GM(1，1)节能潜力预测模型基础上，选择单位产品能耗(t标煤/t)、产品产量(t/年)为预测变量。

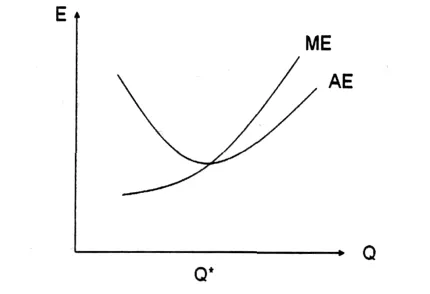
图1 单位产品能耗与产品产量

2.2 基础模型的修正

由于我国自1980年以来不断加强工业企业节能政策工具的使用，因此本文在进行节能潜力预测时不能不考虑节能政策对单位产品能耗和产品产量的影响。此外行业内的先进用能水平也是我们应考虑的一个影响因素。基于此本文提出了基础模型的修正分析。

2.2.1 节能政策的影响

序列数据的发展趋势总是具有一定的惯性，因此可假设序列相邻两个时刻的级比有一定程度的相似性。本文根据国家政策数据发展的估计百分比与原始数列的平均序列级比对序列最后一个数据进行了处理，即

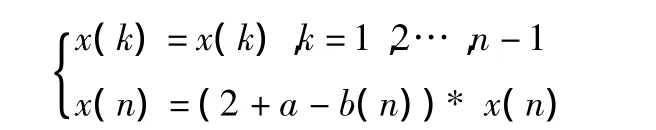
其中

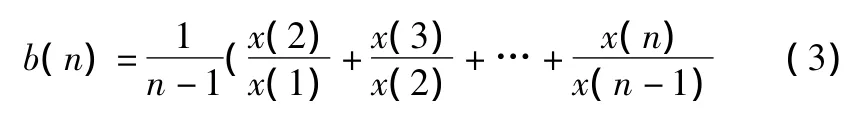
为x在n时刻的平均序列级比。

a为预测时刻根据国家政策预计要将序列数据提高或降低的百分比数。如果国家政策是将数据提高，则a取正值，否则取负值［4］。

2.2.2 行业内先进企业的用能水平的影响

节能潜力是个相对量，在构造节能潜力的判别准则时还需选定个比较标杆。基于此，本文结合了预测企业与行业内先进用能水平的关联度来完善MGM(1，2)模型的预测的结果。

本文采用肖扬提出的灰关联度计算公式［5］，设主因素时间数列和比较因素时间数列分别为X0(t)={x0(1)，x0(2)，…，x0(N)}，Xi(t)={xi(1)，xi(2)，…，xi(N)}

则X0(t)与Xi(t)的关联系数为

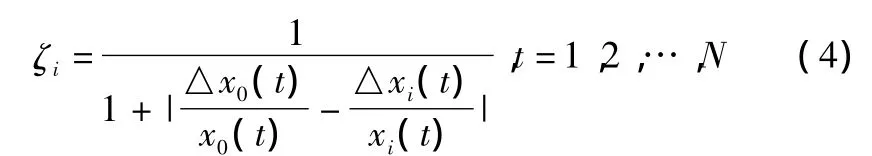
式中△x0(t)=x0(t+1)－x0(t)，△xi(t)=xi(t+ 1)－xi(t)

X0(t)与Xi(t)的关联系数为ζi(t)，X0(t)与Xi(t)的关联度为

2.3 预测模型的最终构建

我们用x1和x2分别表示单位产品能耗与产品产量，令(k)为灰时间序列(k)为相应的一次累加生成序列(i=1，2)，设考虑了节能政策影响后的单位产品能耗序列为(k)，相应的其一次累加生成序列为(k)，则我们可以根据处理后的序列建立MGM(1，2)模型，其矩阵形式为

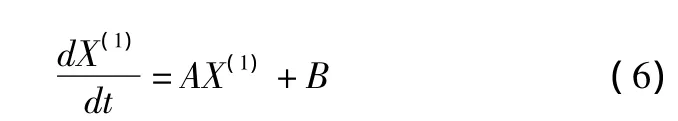
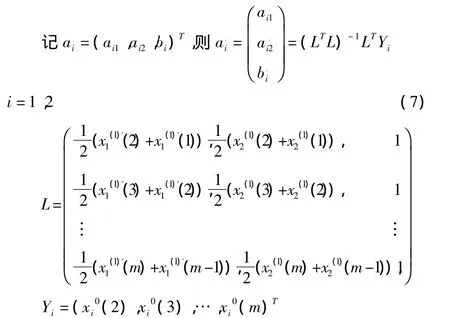
则MGM(1，2)模型的计算值为

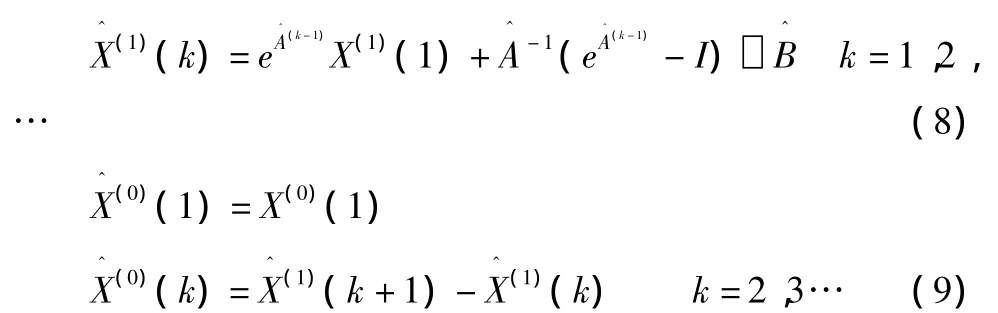
考虑了行业内先进的用能水平后，结MGM(1，2)模型计算的结果可预测工业企业节能潜力

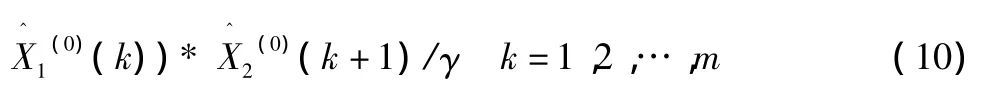
(0)(k)为输入的时间序列最后一时刻的单位产品能耗，

(0)(k+1)为预测年份的产品产量，γ代表预测企业与行业内先进企业的关联度。

3 模型的检验分析

3.1 检验分析的思路

为了能够获得高精度的预测模型，本文采用残差和后验差检验来进行模型模拟精度的分析。

本文的检验思路是:对现实一家皮革生产企业的历史数据进行预处理，然后将处理后的数据输入GM(1，1)模型和MGM(1，2)模型中进行模拟。对两种模型的模拟结果进行检验分析，以证明MGM(1，2)优越于GM(1，1)模型，检验步骤如图2所示。

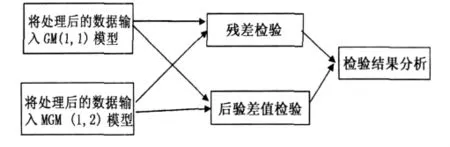
图2 MGM(1，2)模型的检验分析

3.2 原始数据的获取与处理

3.2.1 原始数据的获取

本文选择位于河北省高啤店市白沟镇工业园区内的加元皮革公司1999年至2005年的单位产品能耗、产品产量和历史节能量作为检验模型的数据(见表1)。

表1 单位产品能耗与产品产量原始序列

3.2.2 原始数据的处理

本文假设该家企业为响应国家政策拟定未来1年将企业单位产品能耗减少5%，于是该工业企业的单位产品能耗数据相应变化，经计算2006年的单位产品能耗由1.101t标煤/百码变为1.0794t标煤/百码。

3.3 残差检验

残差检验是对模型的模拟值和实际值的相对误差进行逐点检验，计算公式如下:

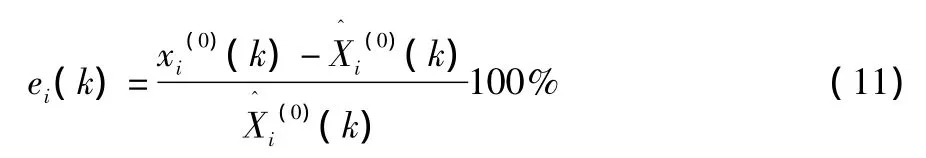
将处理后的历史数据输入到MGM(1，2)模型与GM (1，1)模型，应用matlab软件计算得两模型拟合结果的残差如表2所示。

3.4 后验差值检验

后验差值检验也称为均方差比值

后验差比值为

小误差概率为

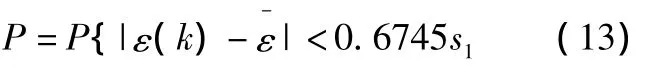
经计算，MGM(1，2)模型单位产品能耗拟合结果的c值为0.1173，p值为1.0，产品产量拟合结果的c值为0.2093，p值为1.0，两个变量的模拟结果精度均属于“好”的等级。而GM(1，1)模型针对单位产品能耗这一变量的c值为0.1248，p值为1.0，模拟精度也属于“好”的等级。

3.5 检验结果分析

残差检验中MGM(1，2)模型拟合的残差明显优于GM (1，1)模型，证明了MGM(1，2)模型的拟合效果要好于GM(1，1)模型的拟合效果。在后验差值检验中，虽然MGM(1，2)模型和GM(1，1)模型的后验差值均属于“好”的等级，但是前者的数值较后者小，这说明MGM(1，2)模型的拟合效果要比GM(1，1)模型的拟合效果好。

3.6 节能潜力预测

3.6.1 关联度γ的求解

据统计数据可知，该行业先进用能水平的单位产品能耗自1999年至2005年依次为0.91，0.83，0.828，0.799，0.72，0.711，0.656t标煤/百码。据此计算得该企业的单位产品能耗与行业内先进水平单位产品能耗的关联度为0.9735。

3.6.2 开元皮革厂2006年节能潜力预测

将处理后的数据输入到MGM(1，2)模型当中进行预测，得2006年开元皮革厂的单位产品能耗为1.0396t标煤/百码，产品产量为94209百码。然后根据论文所构建的节能潜力预测模型得该企业的节能潜力=(1.0794－1.0396)×942091/γ≈3852t标煤。未考虑行业内先进水平的用能情况而计算得2006年的节能潜力=(1.0794－1.0396)×94209≈3750t标煤。

应用GM(1，1)模型进行预测后得2006年的单位产品能耗为1.051t标煤/百码，该企业计划2006年产品产量为99380百码，则节能潜力预测值=(1.0794－1.051)× 99380≈2822t标煤。

据资料显示该企业2006年实际的节能潜力为3829吨标煤，本文所建的预测模型结果达到了很高的精度，预测误差=(3852－3829)/3829≈0.6%。MGM(1，2)模型的预测误差=(3750－3829)/3829≈2.1%。而原有模型的预测误差则为27%。显然，文中所构建的工业企业节能潜力预测模型的精度要远远优于现有的单变量模型和MGM(1，2)模型。

4 结论

MGM(1，n)模型充分考虑了多个变量之间的相互影响关系，克服了常规的回归分析或GM(1，1)单方面预测及定性预测的缺陷。本文基于MGM(1，n)模型提出了多变量的工业企业节能潜力预测模型。在考虑了政策影响后，利用经济学分析方法选定单位产品能耗和产品产量为工业企业节能潜力的预测变量，并且将行业内先进企业用能水平作为标杆完善了MGM(1，n)模型的计算结果，从而提高了工业企业节能潜力预测模型的精确度。

(编辑:刘文政)

［1］钱伟.浅论节能潜力分析方法［J］.应用能源技术.2003(5):34－36.

［2］许圣华.灰色系统理论在企业节能潜力预测中的应用［J］.能源研究与利用.1999(5):31.

［3］翟军，盛建明.MGM(1，n)灰色模型及应用［J］.系统工程理论与实践.1997(5):011，111.

［4］邓聚龙.灰色预测控制［A］.见:灰色系统论文集［C］.武汉:华中理工大学出版社，1989.41－51.

［5］肖扬.动态系统分析［M］.北京:北方交通大学出版社，2002.25－30.

AbstractScientific forecasting of the future industry enterprises’energy-saving potentials is an important basis for developing energysaving policies of industrial enterprises，and is also the important component of the guides to energy-saving management of industrial enterprises.This paper based on the grey system theory，in view of traditional single-variable forecasting model proposed a multi-variable forecasting model of energy-saving potentials in industry enterprises.Through improving the time series，taking the energy-saving policies into account，with the advanced level in the industry as a benchmarking，this paper improved the forecasting and the accuracy of the model.

Key wordsindustrial enterprise;energy-saving potential;MGM(1，n)

Research on the Forecasting Model of Energy-saving Potentials in Industry Enterprises

WANG Xiao-jieZHOU Ying-nanLIU Huan-huan
(School of Management，Dalian University of Technology，Dalian Liaoning 116023，China)

TK018

A

1002－2104(2010)05专－0027－04

2010-07-10

王晓杰，硕士生，主要研究方向为企业法律环境研究。