图的反符号星k控制数

徐保根，孔祥阳，陈悦

(华东交通大学基础科学学院，江西南昌330013)

图的反符号星k控制数

徐保根，孔祥阳，陈悦

(华东交通大学基础科学学院，江西南昌330013)

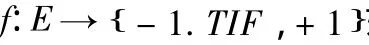
反符号星k控制函数;反符号星k控制数;反符号星控制函数;反符号星控制数

在1998年美国图论学者W T Haynes等人出版了专著，该著作较为全面而又系统地总结了近些年在图论方面的一些重要研究成果。但这些成果几乎都是关于图的点控制问题，与图的边控制问题相关的结果却比较少。为了将图的控制理论内容进行进一步健全和丰富，我们将由对图的点控制问题的研究转向对图的边控制问题的研究，我们已经得到了一些研究成果，例如，符号边控制，符号星控制和符号圈控制等。在本文中，我们将引入一个新概念，即图的反符号星k控制概念。

本文所考察的图均为无向简单图，文中的符号和术语若无特别说明则均与文献相同。

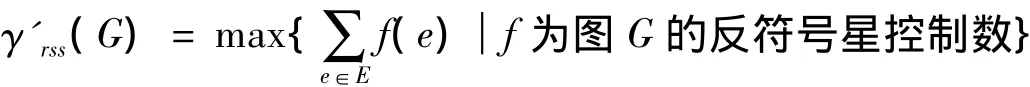
下面我们将图的反符号星控制概念进行推广，从而引入一种新的图的边控制概念。

对于空图，所以反符号星k控制概念既是对反符号星控制概念的一种推广，也是对符号星k控制概念的一种推广。关于图的反符号星控制数，文［6］中指给出了如下结果:

本文在对文［7］中的结果进行了推广——给出了一般图的反符号星k控制数的若干上界，在此基础上，给出了n阶路Pn和n阶圈Cn的反符号星k控制数的表达式。

定理1对于任意n阶图G，当δ≥1，1≤k≤n－1时，有

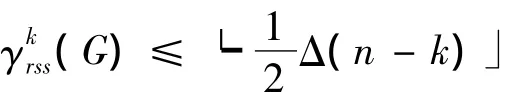
其中:δ=δ(G)，Δ=Δ(G)分别表示图G的最小度和最大度。

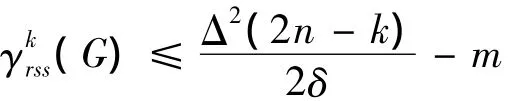
其中:δ=δ(G)和Δ=Δ(G)分别为图G的最小度和最大度。

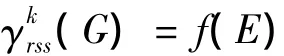
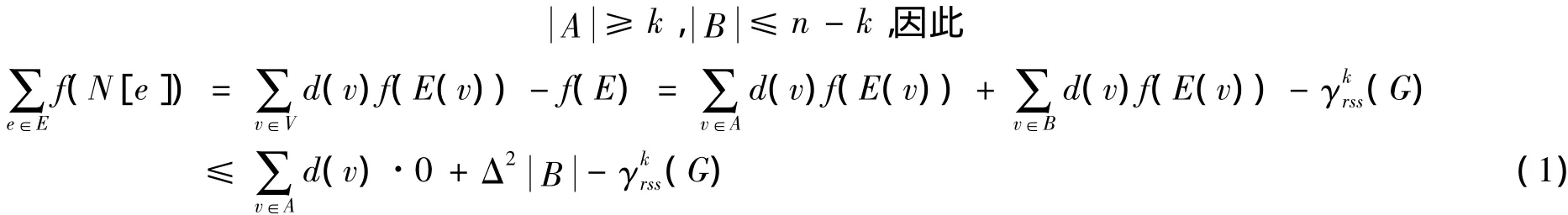
另外，我们还可得到

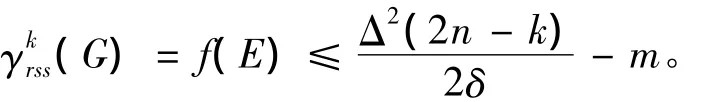
可见结论是成立的，定理证毕。

根据定理2，我们可得到如下推论:

推论对任意n阶r－正则图G，若r≥1，且1≤k≤n，则有

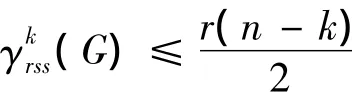
最后我们给出n阶路Pn和n阶圈Cn的反符号星k控制数的表达式。

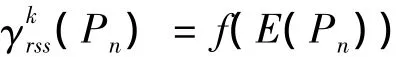
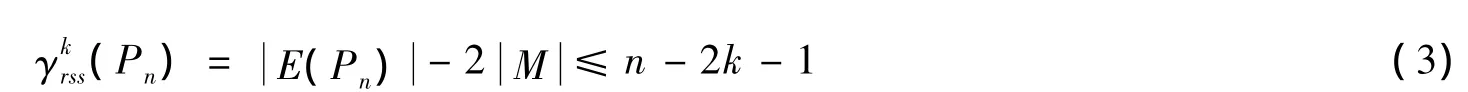
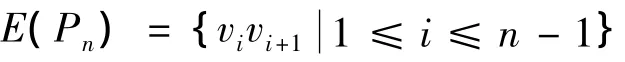
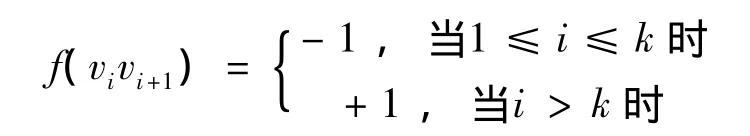
可以验证:f为Pn的一个反符号星k控制函数且有

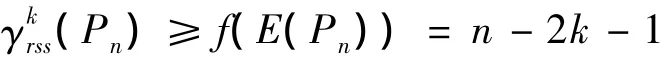
结合(3)知结论(Ⅰ)成立。同理可知结论(Ⅱ)也成立，定理证毕。

［1］HAYNES T W，HEDETNIEMI S T，SLATER P J.Domination in graphs［M］.New York:Marcel Dekker，INC，1998.

［2］XU BAOGEN.On signed edge domination numbers of graphs［J］.Discrete Math，2001，239(1/2/3):179－189.

［3］XU BAOGEN.Two classes of edge domination in graphs［J］.Discrete Appl Math，2006，154(10):1 541－1 546.

［4］XU BAOGEN.On signed cycle domination in graphs［J］.Discrete Math，2009，309(4):1 007－1 012.

［5］BONDY J A，MURTY V S R.Graph Theory with Applications［M］.Elsevier，Amsterdam，1976.

［6］赵华，徐保根，赵金凤，帅春萍.关于图的反符号星控制数［J］.华东交通大学学报，2008，25(5):84－87.

［7］徐保根，李春华.图的符号星k控制数［J］.纯粹数学与应用数学，2009，25(4):638－641.

(责任编辑 王建华)

Reverse Signed Star k－subdomination Numbers of Graphs

Xu Baogen，Kong Xiangyang，Chen Yue

(School ofBasic Sciences，East China Jiaotong University，Nanchang 330013，China)

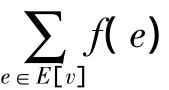
signed star k－dominating function;signed star k－domination number;signed star dominating function;signed star domination number

O157.5

A

1005－0523(2010)04－0068－03

2010－04－25

国家自然科学基金项目(10661007);江西省教育厅科研项目(GJJ09215)

徐保根(1963－)，男，教授，研究方向为图论与组合数学。