可验证的动态多秘密共享

赵丽萍，汤文亮

(华东交通大学软件学院，江西南昌330013)

可验证的动态多秘密共享

赵丽萍，汤文亮

(华东交通大学软件学院，江西南昌330013)

提出了一种新的可验证的动态门限多秘密共享方案。该方案的安全性基于Shamir的秘密共享体制和椭圆曲线加密算法的安全性以及椭圆曲线离散对数问题的求解困难性。共享秘密可以周期性的改变，秘密分发者周期性的改变公告栏上的信息以增强系统的健壮性。对于不同的共享秘密，秘密分发者可以动态调整该秘密的门限值。此外，方案能有效检测和识别参与者的欺骗行为，参与者也可以验证其接受到的信息，且无需改变私有信息在任何时候都可以重构秘密。由于公告栏上的信息是定期更新的，所以不会影响新秘密的共享。

门限;椭圆曲线;秘密共享;多秘密

秘密共享［1］是信息安全和数据保密的重要手段。1979年Shamir［2］和Blakey［3］分别独立地提出了门限秘密共享体制，使授权的合格子集能容易地恢复共享秘密，而非合格子集得不到关于共享秘密的任何信息。由于有着广泛的实际应用前景，许多学者投入了大量精力对其本身和相关问题进行深入的研究，并获得了一批研究成果。在Shamir的秘密共享方案中存在两个问题:庄家(秘密的分发者)的诚实性和成员的诚实性。对这两个问题的研究，就形成了可验证的秘密共享方案［4－5］。随后的大多数方案在设计时都基于2个假设:(1)在秘密被重构之前所有的参与者和秘密都不改变。(2)秘密分发者和各参与者之间需要建立一条安全信道。但这2个假设会影响秘密共享方案的实际应用。文献［6］提出了一种检测方案，一次计算即可知道该授权子集中是否有不诚实的用户。如果没有欺诈者，即可得到正确秘密;如果存在欺诈者，则需要对各个用户进行验证。当参与者中没有欺诈者存在时，验证所需的计算量将大大减少。文献［7］提出了一个动态的秘密共享方案，在该方案中使用了RSA密码体制，这使得方案不需要建立安全信道并且共享秘密和参与者都可以动态地发生变化，但它只适用于单秘密共享，存在一定的局限性。

本文基于椭圆曲线加密体制和Shamir的秘密共享体制，提出了一种新的多秘密共享方案。该方案具有如下特点:(1)可进行多秘密的共享;(2)对于不同的共享秘密，秘密分发者可动态调整其门限值; (3)可防止秘密分发者与参与者的相互欺诈。

1 方案描述

方案由系统初始化、秘密的分发、秘密的重构、秘密的更新4个阶段构成。

1.1 系统初始化

系统中包含一个秘密分发者和n个参与者。用U表示由n个参与者构成的集合，并且U由集合构成，即

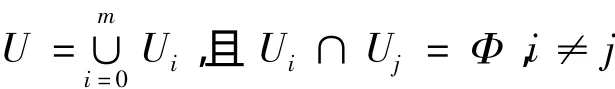
设E(Fq)是一条椭圆曲线，G1是该曲线上的一个α阶子群，其中α为质数。G为α阶循环子群，G2=G－{0}。令e:G1×G1→G2上的双线性映射，秘密分发者选择G1的一个生成子g，同时选择加密哈希函数h: G1→，将＜α，G1，G2，e，g，h＞发布在公告栏，同时公布参与者的数目。秘密分发者随机秘密选取2k－ 1个随机数a0，a1，…，a2k－2，构造多项式［8］:。秘密分发者计算，并将公开。

每个参与者Ui(i=0，1，2，…，n－1)下载公告栏上的信息，随机选取秘密整数si∈，计算公钥Ui=sig，并将Ui发回给秘密发送者，以保证不同的参与者使用不同的密钥。秘密分发者将Ui(i=1，2，…，n－1)公布在公告栏。

1.2 秘密分发

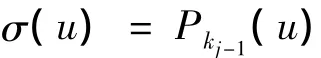
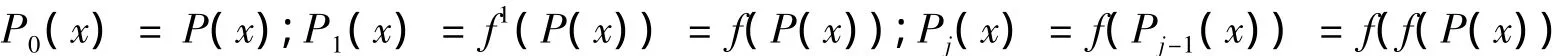
计算

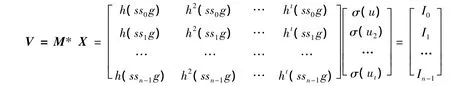
秘密分发者将Ii(i=1，2，…，n－1)公布在布告栏上。

1.3 秘密重构

为了将t份秘密重构，需要t个参与者提供他们的ssig(i=H1，H2，…，Ht)值。每个参与者Ui(i=1，2，…，t－1)首先从公告栏上下载sg，并计算ssig，然后利用哈希函数h生成矩阵M的第i行，最后参与者将该行信息发送给秘密合成者。这样，授权子集内的各参与者合作，可列出方程M*X=I。

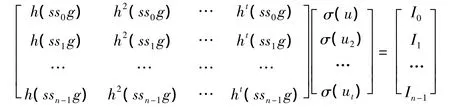
1.4 秘密更新

秘密分发者重新选择共享秘密的门限和参数s，秘密更新如下:

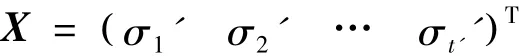
1.5 成员的增加和删除

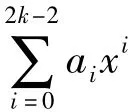
在秘密没有恢复前，如果有参与者因某些原因要被删除。此时秘密分发者将其公开信息从公告栏上删除，然后秘密分发者随机选择s∈，对所有的Ui(i=0，1，…，n－2)，使用哈希函数h，构造一个(n－1)*t的矩阵M，重复执行1.2步骤。

2 分析与讨论

2.1 安全性分析

(1)参与者提供的秘密分量是可验证的，并且验证并不需要复杂的算法或更多的信息。秘密的重构者只需验证e(ssig，g)≡e(sg，Ui)是否成立。如果成立，则参与者提供的信息是有效的，否则信息是无效的。同时也可以识别出无效的参与者。

(2)当多于t个参与者提供其秘密信息时，秘密是可重构的。首先通过等式e(ssig，g)≡e(sg，Ui)来验证参与者提供的信息是否有效，然后将参与者提供的信息进行重构，将秘密恢复。

(3)参与者提交给秘密分发者的信息Ui(=sig)是安全的。由于算法是基于椭圆曲线离散对数问题，所以参与者的个人信息si是不会泄密的。

(4)可检验秘密分发者是否诚实。各参与者在收到自己的子秘密之后，可根据公开的信息，验证式是否成立。如果成立，说明秘密分发者分发的是正确子秘密。这是因为，第j等级的用户的多项式进行kj－1次f函数运算后，多项式中原本次数低于kj－1的项降为0，其后各项分别为kj－1≤t≤k－1。所以有:

2.2 性能分析

(1)与Chen et al.'s秘密共享机制相比，Chen et al.'s秘密共享机制中的共享秘密需通过哈希函数h(rp)生成。在本文的共享机制中，共享秘密的门限值t存储在矩阵M，故大小由矩阵M的大小决定，秘密s在任何时候均存储在矩阵X中，与哈希函数h无关。所以计算时间会缩短。

(2)与Chen et al.'s秘密共享机制相比，Chen et al.'s秘密共享机制中，矩阵M会以(n－t+1)×(n+t)增大，而X矩阵会以(n+t)×1增大，此外，其门限值随着秘密的重构会改变为2t－1;在本文的共享机制中，矩阵M和X的大小不会改变，且秘密更新也非常方便，秘密分发者只需选择新的门限值t′，s′，进而构造新的矩阵M′，X′，V′，I′，故多秘密共享在本方案中所需的空间不会发生改变。

(3)秘密重构的门限是可变的。秘密分发者只需改变矩阵M和X的大小，秘密重构的门限就可以改变。

表1 本文协议与Chen et al.'s协议的比较

3 结论

本文提出了一种的新的多秘密共享方案，该方案允许每个参与者只需保存一个秘密信息就能共享多个秘密。降低了秘密分发者的算法难度。秘密重构时，参与者只需提供公共信息和个人的秘密信息，就可实现秘密的重构。当门限发生改变时，秘密分发者只需调整一个矩阵的大小。此外，该方案对参与者的验证加强了该方案的健壮性。由于方案是基于椭圆曲线，故其安全性较高，算法的效率也较高。

［1］CHIEN H Y，JAN J K，TSENG Y M.A practical(t，n)multi－secret sharing scheme［J］.IEICE Transaction on Fundamentals，2000，83(12):2 762－2 765.

［2］SHAMIR A.How to share a secret［J］.Communications of the ACM，1979，22(11):612－613.

［3］BLAKLEY G.Safeguarding Cryptographic Keys［C］//New York:Proceedings of the AFIPS 1979 National Computer Conference，1979:313－317.

［4］CHOR B，GOLDWASSER S，MICALI S，et al.Verifiable Secret Sharing and Achieving Simultaneity in the Presence of Faults［C］//Proc of the 26th IEEE Symposium on Foundations of Computer Sciences.Los Angeles，USA:IEEE Computer Society，1985.

［5］TASSA T.Hierarchical threshold secret sharing［J］.Journal of Cryptolo－gy，2007，20(2):237－264.

［6］许春香，肖鸿，肖国镇.安全的门限秘密共享方案［C］//第八届中国密码学学术会议论文集.北京:科学出版社，2004: 120－124.

［7］庞辽军，李慧贤.动态门限多重秘密共享方案［J］.计算机工程，2008，34(15):164－165.

［8］毛颖颖，毛明，李冬冬.安全的多等级门限秘密共享［J］.计算机工程与应用，2009，45(32):90－92.

［9］CHEN W，LONG X，BAI Y B，GAO X P.A New Dynamic Threshold Secret Sharing Scheme from Bilinear Maps［R］.In International Conference on Parallel Processing Workshops，2007:19.

(责任编辑 刘棉玲)

Verifiable Dynamic Multi－secret Sharing Scheme

Zhao Liping，Tang Wenliang

(School of Software Engineering，East China Jiaotong University，Nanchang 330013，China)

The paper proposes a new verifiable multi－secret sharing scheme of dynamic threshold.The security of the proposed scheme is based on Shamir＇s secret sharing scheme and the ECIES cryptosystem，and the difficulty in solving the elliptic curve discrete logarithm.In the scheme，the secret will change periodically and the dealer will periodically publish some of the information to increase the robustness of system.The dealer could adjust the threshold value depending on the secure level of different secret.In addition，the efficient solutions against multiform cheating of any participant are proposed，and the participants can verify the information which they have received.Each participant uses his own private secret during different time periods to reconstruct the corresponding shared secrets without revealing their own private information.Public information is renewed periodically in the scheme，which will not influence new secret sharing.

threshold;elliptic curve;secret sharing;multi－secret

TP393.08

A

1005－0523(2010)04－0063－05

2010－03－16

江西省南昌市科技课题经费资助项目(洪财企［2008］68号)

赵丽萍(1981－)，女，硕士研究生，助教，主要研究方向为软件工程、信息安全。