300000 DWT浮船坞的锚泊系统设计
邱崚唐军
(上海船舶研究设计院,上海 200032)
0 前言
300000 DWT浮船坞是大连中远船务有限公司委托我院设计的我国迄今为止最大的浮船坞。
这是一种多根链索泊碇的浮船坞,各链索的水平力分配较为复杂。由于系泊链索是一种柔性连接,因此船体在受到风、流、波浪以及惯性力作用以后,必定会发生位移,从而又改变了与位移量有关的各链索上张力的大小。这就无法从“外力与系泊力平衡”方程中一次求解,而要通过逐次迭代的过程来求解。
浮船坞在系泊状态下受风、流、波浪等环境力作用时,其位置将因之漂移,系泊系统会提供约束力,限制其漂移量的幅度。锚链力的大小是随着挂链点至锚碇点的距离变化而变化的,距离越大锚链受力越大,反之越小。本计算采用锚泊系统专用程序在计算机上完成。该程序采用了准静态方法,浮船坞的最大漂移量由风、流产生的静态平均漂移,浮船坞对波频运动响应及二阶波浪漂移力引起的低频振荡组成,锚链的最大载荷由最大漂移状态下的位置来确定。
1 风、波浪、流环境力计算
1.1 概述
在稳定静态条件下,作用在系泊物体上的环境力包括风力、流力和二阶平均波浪漂移力。石油公司国际海事论坛(OCIMF)在1977年和1994年两次发表了超大型油船的风载和流载计算方法,以其系统完整的模型试验资料,目前已成为各种应用研究的标准载荷计算方法。唯在使用时需注意正确选择各种影响参数,同时还需进行各种修正,如干舷比修正、长宽比修正、纵倾修正等。波浪载荷以三种形式作用在系泊船上:(1)波频振荡的一阶波浪作用力。它是波浪力的主要成份,将引起船的波频运动。这个作用力并不直接作用于锚泊系统上,在锚系受力分析时,它是以由锚链运动(当然因船舶运动产生)产生的动态张力反映出来的。在准静态分析时,假定这个动张力等于静态下由锚链位置产生最大偏中锚泊系统可以得到正确的结果,但在水深超过600 m的深海锚泊系统分析时,准静态方法可能产生较大误差,必须使用动态时域分析法。(2)慢变的波浪二阶力,这是频率很低、量值较小的一种波浪力成份。一旦它的频率和系泊系统的自振频率接近,将引起船作大幅度的纵荡和横荡运动,巨大的船舶惯性力将作用在锚泊系统上。海上锚泊系统的损坏大多数是由它引起的。使用调整锚链预紧力改变系统自振频率的方法,可以有效抑止低频慢漂运动。对于本坞的多锚系泊系统,由于缆索的预紧力较大,不会激发起大幅度的慢漂运动,可以不用考虑。(3)二阶平均波浪漂移力。这是二阶波浪力中的定常部份,和风力和流力一样也是静态力。一般是一个小量,但是它和波高平方成正比关系,一旦波高增大,它将迅速增加。系泊系统环境力中必须要考虑这一因素(特别在外海的系泊系统中)。
1.2 风载荷计算
系泊油船的风力和风力矩按下述公式计算:

式中:
FXW、FYW、MXYW分别为纵向风力、横向风力和首摇风力矩,kN或kN·m;
CXW、CYW、CXYW分别为纵向风力系数、横向风力系数和首摇风力矩系数;
ρW为空气密度,kN·s2·m-4;
VW为海平面以上10 m处的风速,m/sec;
AT为正向受风面积,m2;
AL为侧向受风面积,m2;
LBP为两柱间长,m。
风力系数CXW、CYW、CXYW根据风向角、装载状况及船首形状由OCIMF资料中的图谱得到。
1.3 流载荷计算
系泊油船的流力和流力矩按下述公式计算:

式中:
FXC、FYC、MXYC分别为纵向流力、横向流力和首摇流力矩,kN或kN·m;
CXW、CYW、CXYW分别为纵向流力系数、横向流力系数和首摇流力矩系数;
ρC为空气密度,kN·s2·m-4;
VC为油船吃水范围内的平均流速,m/sec;
T为平均吃水,m;
LBP为两柱间长,m。
风力系数CXC、CYC、CXYC根据流向角、水深吃水比、装载状况及船首形状由OCIMF资料中的图谱得到。
1.4 二阶平均波浪漂移力计算
二阶平均波浪漂移力的计算目前还没有适当的经验公式,我们采用CSSRC的三因次船舶耐波性程序进行计算。此方法虽然计算复杂、数据准备工作量较大,但理论严谨,结果较为可靠。
2 浮船坞的锚泊系统计算
2.1 背景
300000 DWT浮船坞锚泊于大连湾内北侧和尚岛与棉花岛之间的海湾内。本坞首部接新建的300000 DWT修船码头,坞首角为北偏东35°。左舷临近南防波堤,右舷有新建的西防波堤和东防波堤,见图1。
本坞所处的水域只有南偏东15°至南偏东60°夹角为45°的范围内面向外海,而其它方位均受到陆地的良好掩护。因而对该处有影响的波向主要为从外海传入的SE向和SSE向波浪及S向~SW向的小风区波浪。本坞位置处也是湾内水流最弱的区域之一。所以本坞所处的自然环境条件较为优良。但本坞将经受到风速很大的北向风影响。为了合理设计锚泊系统,保证系统安全可靠,特进行本计算。计算的目的是要校核该系统在外界风、波浪、流环境载荷的作用下,其安全系泊的能力以及浮船坞的偏移和锚点受力状况,为引桥和锚桩设计提供基础数据。
2.2 本坞的主尺度数据如下


图1 本工程在厂区位置

2.3 需要校核的工况
根据本坞的使用情况,本计算针对下述的二种工况进行校核计算:
(1)最大风工况。坞内有30万吨级的油船或8100 TEU集装箱船,各方向的风速按历年(1957~1969年统计)各方向的最大风速(下限取为24 m/s)设定,并将此工况作为最恶劣的外界环境条件下。
(2)修船工况。坞内有30万吨级的油船或8100 TEU集装箱船,且右舷还停靠一艘17万吨级好望角型散货船。此工况具有最大的受风面积,但此时设定的风速为气象台风力8级上限,最大风速为20.7 m/s。
2.4 本区域的环境条件
根据业主所能提供的环境资料,同时也考虑了各种安全因素,本区域环境具体的计算条件选定如下:
(1)各根锚链的锚点标高根据水深变化分别取为▽-11.0、-11.5、-12.0、-12.5 和-13.0m, 潮位取校核高水位▽5.10m和校核低水位▽-1.15m二种情况,浮船坞吃水为5.4m,流力计算时平均水深取为12.0m。
(2)风速:在最大风工况时,坞内有30万吨级的油船或8100 TEU集装箱船,坞船联合体的横向受风面积为11363 m2,纵向受风面积为2941 m2。各方向的风速取为历年(1957~1969年统计)各方向的最大风速(小于24 m/s则取为24 m/s),将它作为最恶劣的外界环境条件。
在修船工况时,除了坞内有三十万载重吨级油船之外,坞右舷再旁靠一艘十七万吨级散货船,坞船(包括旁靠货船)联合体的横向受风面积11363 m2,纵向受风面积4269 m2。此时各方向设定的风速均为气象台风力8级上限,风速为20.7 m/s。
因为锚泊系统配置和计算风速对于本坞的左右舷不是对称的,所以本计算对于各种工况均设定16个相对风向角:从 12.5°(SSW)变化到 350°(SW),间隔 22.5°。 0°~180°为右舷风,180°~360°(-180°~-0°)为左舷风,180°为首迎风,90°为正横风,0°为顺风。
(3)流速:工程位置处的海流主要为潮流,且处于潮流最弱处,涨潮流向自东南向西北,落潮流自西北向东南,最大流速小于0.3 m/s。本计算设定最大涨潮流速 0.3 m/s,相对流向 80°;最大落潮流速0.3 m/s,相对流向 260°。
4)波浪:本区域受陆地良好掩护,只有南偏东15°至南偏东60°范围内才有外海传入的较大波浪,而外海的波浪经过湾口折射、浅水和破碎影响,到达工程位置处的波高已大为降低。本计算根据波浪推算和业主意见,设定在最大风工况,工程位置处的最大波浪为 H1%=2.44 m,在修船工况,H1%=0.9 m,根据统计规律相应的有义波高H1/3分别为1.6053 m和0.5921 m;再考虑到本坞左舷紧靠南防波堤,且只有南偏东15°至南偏东60°范围内面向外海,而其它方位均受到陆地的良好掩护,由于波浪的衰减而发生最大波浪的可能性较小。最终确定,对所有风向先以七折的最大波浪作为计算波高,即在最大风工况有义波高取为 H1/3=1.124m, 波浪 T1周期 5.413s; 在修船工况,则设定有义波高为0.414m,相应波浪T1周期为3.282s。 其后,再对 S、SSE、SE 和 SEE 四个方向,取最大波高(1.6053m 和 0.5921m)进行校核计算。
(5)风、流、浪的环境组合
通常,锚泊系统计算需要在各种环境组合条件下进行。由于没有足够的资料来进行风、流、波浪的方向组合,故考虑最有可能的恶劣的迭加条件。从工程应用的角度,这可保证系统的安全性。在本报告中,以风速风向的变化为主要的变量,并假定波浪在相对波向角30°~90°之间变化,各方向下的波浪取相同的设定波高和周期 (七折最大波高),在S、SSE、SE和SEE四个方向,还进行了最大风和最大浪组合的校核计算。潮流考虑为往复流,相对流向为80°或260°。总环境力以风力为主,然后迭加进在考虑方向范围内的最大波浪漂移力和流力,使环境力的绝对值达到最大。
表1列出了环境条件的各种组合。表中A组合表示最大风工况,B组合对应于修船工况。

表1 三十万吨级钢质浮船坞环境条件组合表
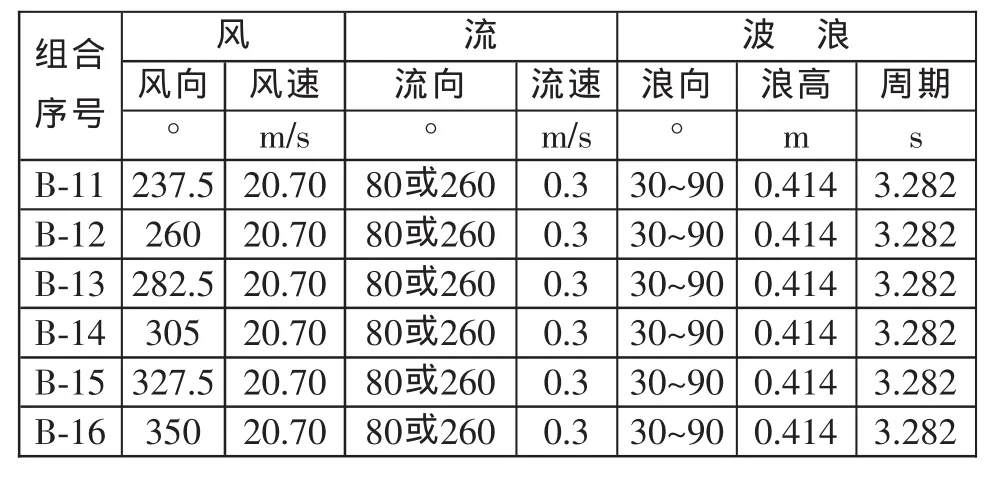
波 浪风向 风速 流向 流速 浪向 浪高 周期°m/s °m/s°m s B-11237.520.70 80或260 0.3 30~90 0.414 3.282 B-12 260 20.70 80或260 0.3 30~900.414 3.282 B-13282.520.70 80或260 0.3 30~900.414 3.282 B-14 305 20.70 80或260 0.3 30~900.414 3.282 B-15327.520.70 80或260 0.3 30~90 0.414 3.282 B-16 350 20.70 80或260 0.3 30~900.414 3.282组合序号风流
2.5 锚泊系统计算的坐标系统
如图2所示,采用右手直角坐标系统,原点在船中心,X轴正向指向船首部,Y轴正向指向左舷,X-Y平面在未受扰动的静水水平面内,方向角定义为风、浪、流的传播方向与OX轴正向之夹角,迎风(浪、流)为 180°。

2.6 该坞的环境力计算
计算得到最大风工况时的风、浪、流静态环境载荷的计算结果,见表2,同时也给出了各种环境组合下的总环境力,表中附图表示总环境力与相对风向角的变化关系。从计算结果可以看到,对本坞而言,最主要的环境力是由风引起的,流力和平均波浪漂移力相对来说均是小量,同时,最大的纵向力发生在北风向 (215°),最大的横向力也发生在北风向(215°),因为此风向的风速最大(34.0 m/s);而最大的摇首力矩则发生在30°~60°的船尾来斜风方向。
表3给出了修船工况时环境力的各种计算结果,其结论与最大风工况相同。必须指出,尽管修船工况时有较大的受风面积,但因要考核的风速较低,最终所受到的环境力要比最大风工况小,由于在这二种工况时的锚泊系统是相同的,所以在以下的计算中,仅对最大风工况进行详细校核计算,假如在最大风工况下锚泊系统是安全的,则在修船工况锚泊系统就更加安全。

01.2)况 最工(大风荷算计载浪、流60、08.8风09.080201坞0.070.4-954.02-0.0-20-船00浮618000.00质0.050.0015-钢150级5630吨.0.22000.0-0120万0320016.02530020-1.40.00900.01.6920.0表228900.0800.43.980.230.044.0010.79-601.12-186-5800.03650.42.0584030.94.23110.8-69-3034000.23大300.0410.06.3-.124最0)移移矩)数漂 力数系荷均漂均)荷艏系·m)系(t 矩)荷数))载(m (t/s矩 载(t)平 平/s摇高载流(m(m 力 力 力(° 力 力 力 浪 (°浪 浪 均波流角流 流流 流流 波.124.124平).124风速速向义向向0.3向向0.3艏艏0.3角波)向向(t 1=波 )向(t 1=浪1=流风流有纵浪纵力纵=Vc 横 横=Vc 摇 摇=Vc H1/3横力H1/3·m波 (t H1/3

2表续

)况工船(修荷算载计流浪、、60风.00.070.42954.020090.08008--坞-.8201-船0浮600质180.050-0.00钢0.0015150级吨.0302056.20万0-.00120002533.020303.4160.01-09000.002.60.0表080280.230.0900.43.980.044.0010.0-600.132.2873--50.03800.42.0586203.2200.314.29-8-00.060000.230.730.0432.30.4140-移移矩))漂漂力(t 系(t荷数均 均)艏系·m 数(m 系 矩 载)荷载数矩))(°/s平(°)摇载(m(t高/s流力力力(m荷力 力力 浪浪 浪 均流波 角 流0.3流流流波.414.414平).414风速向速向)平向义0.3向 向 艏流艏0.3角波)向向(t =0波 )向(t =0浪0=流风流 纵有=Vc纵横横=Vc 摇 摇=Vc 浪纵力横力H1/3波 (t H1/3·m H1/3

2.7 锚泊系统
2.7.1 锚泊系统布置
图3为300000 DWT浮船坞锚泊系统布置图和相应的锚链编号。具体的锚点位置和导缆口的坐标位置列于表4。


表4 锚点和导缆口的坐标位置(最大风工况和修船工况)
2.7.2 主要特征
(1)锚泊锚链数:20根,左右舷不对称布置。
(2)锚索形式:全锚链形式,根据长度、直径和高度的不同分成七种类型。不同类型的锚索具有不同的静特性。
线型 1:1#,20#。
线型 2:3#,4#,5#。
线型 3:6#,7#,16#,17#。
线型 4:8#,9#。
线型 5:10#,11#,12#,13#,14#,15#。
线型 6:18#,19#。
线型 7:2#。
(3)锚链参数和预张力(高潮位 5.10 m):

锚链预张力(t)线型 1 101.14 73 10.7 0.1061 21.03线型 2 105.28 73 11.2 0.1061 19.79线型 3 170.32 73 11.7 0.1061 20.30线型 4 170.41 73 12.2 0.1061 20.34线型 5 170.51 73 12.7 0.1061 20.37线型 6 170.36 73 11.2 0.1061 17.34线型 7 95.47 73 11.2 0.1061 15.61锚索类型锚链长度(m)锚链直径(mm)垂向展伸(m)锚链水中重量(t/m)
2.8 锚泊系统计算
2.8.1 锚链静特性计算
锚链静特性是锚泊系统准静态分析时最基础的计算内容。它反映了在特定深度下的悬链线锚链,其水平伸展(泊距)和线上张力、张角、锚点上拔力等各种量之间的关系。影响这种关系的基本参数是锚链长度和直径、锚链重量,锚链刚度和锚链的垂向伸展(锚点到导缆口的垂向高度)。表5给出了线型1锚链在高潮位+5.10 m时的静特性计算结果;其它线型锚链及在低潮位-1.15 m时的七种锚链线型静特性计算结果本文且不表示。
表中符号表示:


表5 线型1锚链的静特性曲线(高潮位5.10 m)
2.8.2 船舶在波浪中的运动
在用准静态方法方析锚链受力时,需要考虑船舶在波浪中的运动,以便求得各根锚链的最大水平跨距(泊距)。浮船坞在不规则波中的一阶波浪运动也可用CSSRC的船舶运动预报计算机程序算得,计算时忽略了锚链力对船舶运动的影响,因为锚链张力与一阶波浪力相比属于是小量。计算结果给出在表6中,表中数据是单幅运动有义值,相应于2倍均方差。在计算锚链的最大泊距时,按纵荡、横荡和首摇运动的有义值迭加,没有考虑它们之间的相位差,认为有义值的迭加可代表最大泊距。
2.8.3 静态偏移、最大偏移和锚泊系统载荷分析
一个锚泊系统,根据锚点和导缆口的布置情况,以及确定的锚链长度,处于初始的平衡位置,此时各根锚链上的载荷为预张力。在风、浪、流环境力的作用下,系统将偏离初始平衡位置,到达新的平衡位置,并且围绕新的平衡位置作一阶波浪运动。本计算使用准静态分析方法来预估锚泊系统上的载荷,计算方法如下:
(1)首先,根据锚链布置方向和确定的锚点位置,调整锚链长度,使各根锚链达到规定的预张力,系统处于无载平衡位置。
(2)在风力、流力和波浪二阶平均漂移力的作用下,系统发生静态偏移。其新的平衡位置,由环境力和锚泊系统的恢复力相互平衡而确定。
(3)在静态平衡位置,系统还要作一阶波浪运动。在平衡位置上迭加波浪运动,求得系统可能的最大偏移位置。
(4)在系统的最大偏移位置处,计算各根锚链的最大泊距,并根据锚链的静特性曲线,求得系统中各根锚链上的张力和锚点上拔力等各量。
2.8.4 锚泊系统载荷计算
对应于表1中A1~A16环境组合的程序计算输出结果汇总于表7A(最大风工况,高潮位5.10 m),汇总表给出了各根锚链上的最大锚链张力和锚点上拔力。
对低潮位-1.15 m情况作了同样的计算,对应于表1中B1~B16环境组合的程序计算输出结果汇总于表 7B(最大风工况,低潮位-1.15 m)。

表6 300000 DWT钢质浮船坞波浪中运动计算结果


)m 5.11-位潮低最、况工风大最(总汇算计力拔上点锚和力张链锚B 7表
表8则汇总了最大风工况时,在高潮位5.10 m和低潮位-1.15 m二种情况下坞位的偏移量。

表8 坞位偏移计算汇总(最大风工况)
2.9 计算结果分析
(1)高潮位(+5.10 m)时,无载作用下锚泊系统计算得到锚链预张力。程序设定同一线型的锚链的预张力相同,计算得到各锚链的预张力见图4,锚块的上拔力均大于零,即无躺底链长,所以在浮船坞挂链施工时,挂链力(即预紧力)应按图4设定。
浮船坞悬链实长应按图5设计。

图4

图5
(2)高潮位(+5.10 m)时,最大风工况 A1~A16环境组合的程序计算,其中A-10环境组合时受外力最大,部分链张力也最大,各链张力见图6。

图6
(3)高潮位(+5.10 m)时,对于修船工况(B1~B16)环境组合,尽管因有旁靠船而增大了受风面积,但因考核风速较低,总的环境力比最大风工况要小,所以从锚链强度考虑,只需校核最大风工况,无需再校核修船工况。
(4)低潮位(-1.15 m)时,计算得到各锚链的预张力,锚块的上拔力均大于零,即无躺底链长,锚链平衡拉力见图7。

图7
(5)低潮位(-1.15 m)时,对于修船工况(B1~B16)环境组合,因考核风速较低,总的环境力比最大风工况要小,所以从锚链强度考虑,只需校核最大风工况,无需再校核修船工况。
(6)高潮位(+5.10 m),低潮位(-1.15 m) 最大风工况作用下各锚链最大力见图8。

图8 浮船坞锚泊系统布置
3 结语
对三十万吨级钢质浮船坞进行了最大风工况和修船工况二种工况的环境力计算,计算时采用的风、浪、流环境组合均属于严厉状况。结果表明,在总环境力中,风力占主要成份,波浪漂移力和流力仅属小量,最大风工况是最严峻的环境条件,所以在锚泊系统分析时,最大风工况为主要对象,进行了360°相对风向角的校核计算。考虑到在低潮位时,锚链预张力将降低,可能有较大的坞位偏移,所以也进行了低潮位的校核计算。其结论是:
(1)本坞在最严峻的最大风工况,在各种相对风向角下,锚链的最大张力为 156.94 t(3# 锚链),若按照锚链强度的安全系数最小为2.0的规范规定考虑,同时再考虑到锚链预紧力的不均匀程度,则建议2#、3#锚链使用Ø73的三级新链 (最大允许拉力为203 t),1#、4#、5#、9#、12#、13# 和 20# 锚链使用 Ø73的二级新链(最大允许拉力为142 t),其余锚链则可使用73的二级旧链(最大允许拉力为113 t,按二级新链强度的0.8考虑)。本坞的锚链强度满足规范要求,并略有裕度。
(2)本坞在最大风工况下,1#、2#、3#、4#、5# 和20#锚链的锚桩将受到上拔力作用,最大为10.99 t。这是因为上述锚链处于 N向(34 m/s)和 NNW(28 m/s)的强风力作用下,并且其长度较短的缘故。其它锚链不受上拔力作用,有部分锚链躺地。考虑到当前使用的最大风资料仅是1957~1969年的统计数据,有些方向的风速似乎偏小,故将锚链长度作为安全裕度考虑而不于缩短。
(3)本坞在最大风工况(高潮位 5.10 m)时,坞位的最大偏移发生在90°附近的横风向,此时横向偏移可达0.924 m,在0°附近的顺风向,发生最大纵向偏移,最大偏移量为0.619 m,绕Z轴的转动角最大为0.274°,发生在30°尾斜风方向。增加锚链预紧力可以减小偏移量,但将增大锚链张力和锚点上拔力。
(4)在锚链长度和锚桩位置不变情况下,潮位变化将影响锚链静特性和锚链预紧力。在同样的最大风工况下,潮位从5.10 m降低到低潮位的-1.15 m时,锚链的预紧力从20 t左右(见3.2锚链参数和预张力表)降至2 t~3 t左右,这使得X方向的偏移从0.619 m 增大到 1.204 m,Y 方向偏移从 0.924 m 增至 1.427 m,转动角则从 0.274°增至 0.341°。 对于锚链最大张力,主要受锚链静特性的影响,当潮位降低时,锚链的静特性曲线在泊距较小时变软,泊距较大时变硬,所以最大张力减小和增加均有可能,对本坞的情况,当潮位从5.10 m 降至-1.15 m时,锚链的最大张力从 156.94 t降至 153.71 t(详见表 7A 和表7B)。
(5)本坞在修船工况时,尽管受风面积比最大风工况增加,但由于要考核的风速降低,且风力与风速成平方关系,所以总的环境力比最大风工况要小。而二者的锚泊系统布置是完全相同的,所以可以认为,只要系统在最大风工况是安全的,则在修船工况肯定要更加安全。
(6)本坞的首链(1#、20#)和首部左舷链(2#、3#、4#、5#)长度受锚桩布置限制,取的比较短,并且处于34 m/s北风向的强风力作用下,造成了产生较大的锚点上拔力和锚链张力。从强度考虑,它们是最危险的,所以必须使用Ø73的新链。此外,本坞锚泊系统的预紧力取的比较大,这使得坞位的偏移量大为降低,这种系泊方式适合于风流影响大而波浪影响小的环境场合(本坞属这种情况)。但是必须明白,在波浪影响大的场合,紧固方式系泊不宜采用,换言之,如果波浪很大,已使船体产生明显的运动,则降低预紧力可以减小船体运动和锚链张力。
(7)在 S、SSE、SE 和 SEE 四个方向上,最有可能发生最大风和最大浪的环境组合,对这四个方向(相对风向角35°-102.5°)的最大风和最大浪组合情况进行校核计算。结果表明,考虑最大浪高后 (H1/3=1.6053 m),影响最大的是12#锚链,锚链最大张力为 144.88 t(最大风工况,最低潮位-1.15 m,相对风向角 80°), 原来计算值 (在 H1/3=1.124 m 时)为126.65 t。比较二者的计算结果可知,最大张力的增加,主要是由船舶运动的增大而引起的,而静态的波浪漂移力增加的影响仅是小量,这个结论对其它三个方向也是正确的。最大风和最大浪环境组合的校核计算表明(仅在上述的四个方向上),前面的结论仍然适用。
(8)本计算没有给出其它方向的最大风和最大浪组合计算,但在锚泊系统的初步分析和设计时,曾对N向进行了估算,结果表明,2#锚链的强度不能满足要求。必须注意,前述的结论和设计有二个前提,一是在最大风工况时,除了S、SSE、SE和SEE四个方位使用了最大浪组合外,其它方位都假定浪高是最大浪高的0.7倍,相信这是一个合理的假定;二是2#锚链的预紧力已人为地有意减小至15.61 t,而相邻的 3#、4#、5# 锚链之预紧力是 19.79 t, 在锚链预紧力调整时必须充分注意。

