人与动物和平共处的数学模型

高万学

（湖北职业技术学院护理学院，湖北 孝感 432000）

人与动物和平共处的数学模型

高万学

（湖北职业技术学院护理学院，湖北 孝感 432000）

生态环境；数学模型；稳定

1 问题的提出

随着人口数量的剧增，人类生存空间的扩大，人类对动物虐杀程度的加剧，人们留给大自然与动物的生存空间越来越小，动物为了求得生存，对人类发起了一次又一次疯狂的进攻，从20个世纪致命的埃博拉、艾滋病，到21世纪初肆虐全球的SARS、禽流感、甲型H1N1流感以及卷土重来的西尼罗病毒，大量的传染性疾病在世界各地不断暴发。这些病毒有一个共同点就是它们都来自于动物。如果人类想要健康地生活，就要学会与动物和平共处。以下就人与动物和平共处建立数学模型，从数学的角度分析人与动物和平共处的条件。

2 模型的建立

设 t时刻人与动物的数量分别为 x（t），y（t），当他们单独在自然界中生存时，数量的变化符合Logistic[1]模型，于是t时刻人口数量的变化率为：，其中λ1是人口固有增长率，N1是环境允许生存的人口数量的最大值。一方面反映了人口数量的增加对其自身增长的阻碍作用，另一方面，由于动物生存环境的限制，制约了人口数量的增长率，因此在因子中应再减去一项，该项与动物的单位数量成正比，比例系数为α1，于是得到人口数量的增长模型为：

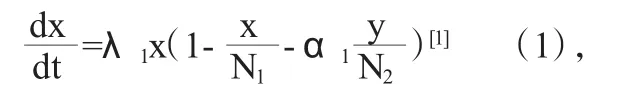
同理，动物数量的增长率为：

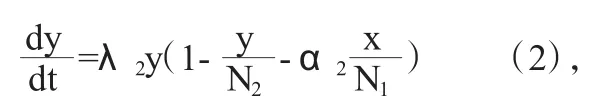
这里 λ2、N2、α2的涵义同方程（1）。

在人与动物的相互竞争中，α1，α2是2个关键的指标，若α1＞1，则单位数量动物消耗资源超过单位数量人类消耗资源，人类在这场竞争中处于劣势，如人类发展的初期；若α2＞1，则单位数量人类消耗资源超过单位数量动物消耗资源，人类在这场竞争中处于优势。

3 稳定性分析

为了研究人与动物在相互竞争中的结局，即t→∞时，x（t）、y（t）的趋向，对方程（1）与方程（2）进行稳定性分析，解方程组：

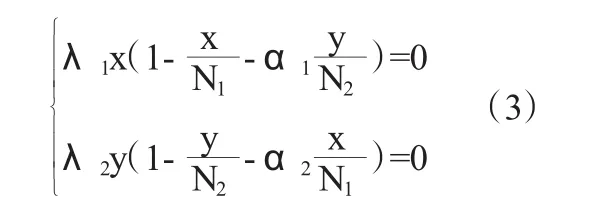
由微分方程的稳定性理论可知，4个平衡点的稳定性情形（见表1）。

表14个平衡点的稳定性情形

4 结果解释

（1）α1＜1，α2＞1时，意味着人与动物在自然界的相互竞争中，动物处于劣势，人类处于强势地位，于是随着时间的推移，动物最终灭绝，人类发展达到自然所能容许的最大容量。

（2）α1＞1，α2＜1 时，结果与（1）正好相反。

（3）α1＜1，α2＜1时，因为在竞争人类所占有的自然资源时动物较弱，而在竞争动物所占有自然资源时人类较弱，于是达到了一个双方共存的稳定的平衡点P3。

（4）a1＞1，a2＞1时，因为在竞争人类所占有的自然资源时动物较强，而在竞争动物所占有自然资源时人类较强，于是平衡点P3不稳定。

随着科技的进步，人口数量的剧增，森林受到破坏，植被逐渐减少，大量的动植物减少，相当数量的物种濒危或灭绝。目前，全世界约有10%～15%的动植物受到威胁，在我国甚至达到15%～20%，高于世界水平[2]。如果人类对自然资源的消费程度和破坏活动不加以控制，那么物种的消失速度将由每天一种提高到每小时一种，比物种自然消失的速度要快1000倍以上[3]，在不久的将来，地球上就只剩下人类，这正是上述结果（1）所描述的。由于大量野生动物的濒危或灭绝，因此以野生动物为宿主的各种病毒将寻找新的宿主——家养动物或人类，于是人类的各种灾难便开始了。为避免这种情况发生，人类在开发利用自然的同时，应注意对自然的保护，谋求一种和谐的、有计划的发展，与自然共生共存，也就是上述结论（3）的情形。

[1]姜启源，谢金星.数学模型[M].第3版.北京：高等教育出版社，2003.

[2]颜锋.奏想绿色的乐章——人与自然[M].北京：北京教育出版社，1999.

[3]贾放.报应：人与自然的失衡[M].北京：中国林业出版社，1999.

G420

A

1671-1246（2010）120-0154-02