大型空冷汽轮发电机定子不对称支路绕组设计与解析分析

李金香，孙玉田，田 昕，焦晓霞

（哈尔滨电机厂有限责任公司, 哈尔滨 150040）

大型空冷汽轮发电机定子不对称支路绕组设计与解析分析

李金香，孙玉田，田 昕，焦晓霞

（哈尔滨电机厂有限责任公司, 哈尔滨 150040）

本文采用解析法对定子不对称三支路绕组进行分析后，提出了能够设计成不对称支路绕组的条件，指出不对称支路绕组是一种对称绕组，其绕组分布系数可按常规绕组分布系数计算。提出了同相位不对称支路绕组（以下简称为同相位）和非同相位不对称支路绕组（以下简称为非同相位）的概念，指出电势不对称度和绕组环流附加损耗（以下简称为环流损耗）是评价不对称支路绕组性能的重要指标。文中还给出了计算环流损耗的解析方法，在损耗计算时应使用定子绕组漏抗而不是交（直）轴电抗。文中给出的各计算公式和方法可直接用于电机的初步设计，具有很高的实用价值。

不对称支路绕组；同相位；非同相位；电势不对称度；绕组环流附加损耗

1 前言

空冷汽轮发电机以空气为冷却介质。由于空气的冷却能力相对较差，降低损耗、提高散热能力尤为重要。对于定子绕组，一个重要措施是降低电压，减薄绝缘，提高散热能力，但这需增加电机的额定电流以保持出力；另一个重要措施是减少定子绕组的损耗（基本铜耗和附加铜耗）。而大型汽轮发电机中常用的，诸如定子线棒采用各种换位方式，以减少股线间环流引起的附加损耗等措施已不能满足空冷电机的要求，因此需设法增加并联支路数，降低线棒的工作电流，减少基本铜耗。对于两极汽轮发电机来说，采用多于 2的并联支路数，如3支路、4支路和6支路等。增加并联支路数，可以减少每支路的电流，使槽电流和线棒电流减小，这不仅可以减少线棒基本铜耗，还能减小绕组电磁力，有利于绕组固定，提高电机的可靠性。但电机额定电流会增大，使铜环引线和母线的用铜量增加，从而增加电机的成本。

人们已对不对称支路绕组进行了一些研究[1，2]，主要是针对水轮发电机的，未给出绕组的支路电势不对称度计算式和绕组分布系数的计算式，给出了绕组环流损耗，但计算环流损耗时采用的电抗不正确。

本文以72槽、二极、空冷汽轮发电机为例，采用解析法进行分析，全面详实地给出不对称三支路绕组的多种设计方案、绕组分布系数计算、电势不对称度计算、环流计算方法及其所用电抗类型。文中给出的计算公式和方法可直接用于电机的初步设计，具有很高的实用价值。

2 定子绕组的设计要求和分析方法

2.1 定子绕组设计的基本要求

空冷汽轮发电机（二极）三支路定子绕组的基本要求与其常规对称定子绕组基本要求一致，分别是：

➢ 在一定导体数下，获得较大的基波电势和基波磁势。

➢ 电势和磁势波形力求接近正弦，即要求电势和磁势中谐波分量尽可能小。

➢ 用铜量少，绝缘性能和机械强度可靠，散热条件好。

➢ 制造工艺简单，检修方便。

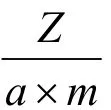
2.2 定子绕组分析方法

对定子绕组进行分析有两种方法，即解析方法和数值分析方法。本文详细阐述解析方法，这是因为解析方法可以方便地用于电机的初步设计中。数值分析方法会在后续的文章中详细阐述。

① 解析方法

首先绘制槽电势星形图，然后根据第2.1节的要求进行分相，最后计算支路电势和绕组系数，并绘制绕组展开图。

② 数值分析方法

采用有限元方法分析计算绕组的支路电势、电势不对称度、支路环流及其环流损耗。

3 不对称支路绕组的设计和解析分析

3.1 不对称支路绕组设计

图1 不对称支路绕组

本文以空冷汽轮发电机（主要数据详见附录）为例，给出定子三支路绕组的同相位（又分为同相位1、同相位2和同相位3）和非同相位绕组的排列方案 ，如表1所示，此表是根据槽电势星形图得出的，由于篇幅限制，此处未给出。同相位2的绕组接线图如图2所示。从表1和图2可见，同相位2的绕组接线规律性强，每根线棒均匀一致；而同相位 1的每根线棒虽然一样，但需在线棒端部进行调整，两个支路的接线规律与另一支路的接线规律不同，容易造成错误。也就是说，同相位2绕组的制造工艺性和嵌线工艺性好，且制造简单。

从表1中可见，同相位1采用了第二条并联支路的所有线棒和第一条支路的一半线棒布置在第一个极下，第三条支路的所有线棒和第一条支路的一半线棒布置在第二个极下；同相位 2采用了第一个极的排列顺序为1—2—3—1—2—3……，而第二个极的排列顺序为 3—2—1—3—2—1……；同相位 3 采用了1—2—3—1—2—3……和 3—2—1—3—2—1……交替排列的方式。从形式上看同相位的几种方式有所不同，但实质上都属于同相位排列方案。

表1 72槽不对称三支路绕组排列方案

图2 同相位2的绕组接线图

3.2 电势、电势不对称度和绕组分布系数计算

根据参考文献[1]和上节中不对称支路绕组设计原则可知：

（1）同相位

同相位每条并联支路电势相位相同、幅值不同，电势相等的两条支路电势（假定为第一支路和第三支路）为：

最大支路（假定第二支路）电势为：

电势不对称度为：

对于分布绕组来说，合成电势等于各线圈电势的矢量和，比各线圈电势直接相加小。绕组的分布好像是减少了它的有效匝数，分布绕组的感应电势等于相应集中绕组的感应电势乘上一个系数，这个系数称为分布系数。根据分布系数的定义，支路 2的绕组分布系数的计算式如下。

支路1和支路3绕组分布系数为：

若忽略同相位各支路间的环流，其绕组分布系数可按下式计算。

绕组分布系数：

（2）非同相位

非同相位每条并联支路电势大小相等，但彼此相位差一个槽距角，支路电势为：

电势矢量差最大值为：

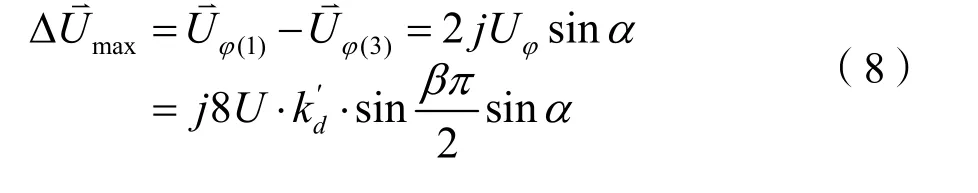
电势不对称度为：

支路绕组分布系数为：

绕组分布系数：

式(1)～式（11）中各量意义如下：

α为槽距角，β为短距比，q为每极每相槽数，α′为每一支路相邻线棒间的槽距角，q′为每极每相每支路槽数，U为上层或下层q′个集中线棒的电势和，Uφ为支路电势，ΔU为电势不对称度，kd绕组分布系数，k′d，kd(1,2,3)为支路绕组分布系数。

（3）绕组分布系数和不对称度计算

根据式（1）～式（11）计算了支路绕组分布系数以及绕组分布系数，如表2所示；绕组电势不对称度，如表3所示。

表2 支路绕组分布系数及绕组分布系数

表3 基波电势不对称度（%）

绕组系数为分布系数和短距系数之积，由于绕组的节距可能有多种选择，故此处给出绕组的支路分布系数和绕组分布系数更有意义。从表 2可见，不对称支路绕组分布系数与常规绕组分布系数相同，这说明其可按常规绕组分布系数计算公式计算，这点意义很大，其证明如下。同时还说明不对称支路绕组的感应电势与正常绕组的相同，绕组的感应电势没有因为支路不对称而减小。

常规绕组分布系数为：

从式（4），（6）和式（10），（11）及 α′和 q′的意义可知，不对称支路绕组分布系数为：

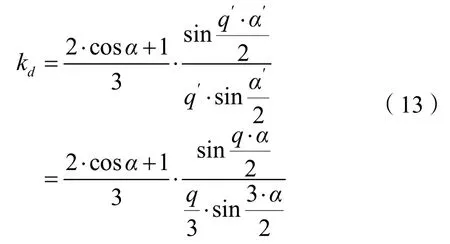
3.3 环流损耗计算

此处以同相位不对称支路绕组空载为例，对环流损耗进行计算[2，3]。每相三支路电路图如图3所示。由于空载定子绕组内的环流产生的磁通不穿过转子和转子绕组，因此图3中x代表每支路的漏抗而不是参考文献[3]中使用的定子绕组每支路直轴电抗。根据发电机的特点，定子漏抗远大于定子电阻，所以电路中忽略了电阻的影响。假定每支路的漏抗相等，由图3可知x=3·xl，其中x为每支路漏抗，xl为每相绕组漏抗（不包含端部漏抗）。

根据式（1）、（2）和式（5）知支路电势差为：

式中：UN为额定电压。

根据图3和电路原理，电流、电势满足如下方程，写成矩阵形式为：

求解方程（15）可得支路电流和环流损耗，见表4。

表4 支路电流及其绕组环流损耗

图3 空载每相三支路绕组电路图

该环流损耗仅为环流基波产生的损耗，未考虑谐波的影响。此损耗很小，与电机总损耗相比，可以忽略不计。

4 结论

本文提出了能够设计成不对称支路绕组的条件为每相每支路的线圈数（或至少线棒数）应为整数，指出了不对称支路绕组是一种对称绕组，其绕组分布系数可按常规绕组分布系数计算。提出了同相位不对称支路绕组和非同相位不对称支路绕组的概念及设计方法和具体实例，指出电势不对称度和环流损耗是评价其性能的重要指标。文中还给出了计算环流损耗的解析方法，指出应使用定子绕组漏抗而不是交（直）轴电抗。文中给出的计算公式和方法可直接用于电机的初步设计，具有很高的实用价值。

附录 大型空冷汽轮发电机主要数据

[1] 朱元巢. 水轮发电机采用不对称绕组初探[J]. 大电机技术, 1988, (4).

[2] 郑小康. 用单根线棒连接法增加水轮发电机可选的对称支路数[J]. 大电机技术, 1989, (3).

Design and Analytical Study of Asymmetric Parallel-circuit Stator Winding for Large Air-cooling Turbogenerator

LI Jin-xiang, SUN Yun-tian, TIAN Xin, JIAO Xiao-xia
(Harbin Electric Machinery Company Limited, Harbin 150040, China)

The condition at which Asymmetric Parallel-Circuit Stator Winding (APSW) can be designed is presented in this paper, based on analysis of APSW by analytical method. It is shown that APSW is symmetric winding, its distribution factor is calculated by the formula of conventional winding. The concept of the same phase angle (SPA) and the different phase angle (DPA) of every parallel-circuit are proposed. SPA has some advantages to DPA, thus SPA will be used in the machine design. The performance of APSW is evaluated by EMF asymmetric ratio and additional losses of circulating current in the winding. Additional losses can be computed by analytical method,and leakage reactance of stator winding should be used in the calculation instead of d-axis and q-axis reactance. All formula and methods can be applied to the primary design of turbogenerator directly,and it is convenient and reliable.

APSW; SPA; DPA; EMF asymmetric ratio; additional losses of circulating current in the winding

TM307

A

1000-3983(2010)01-0001-04

2009-08-03

李金香（1965-），1988年毕业于西安交通大学电机专业，获学士学位，2005年获哈尔滨工业大学电气工程专业工程硕士学位。现从事电机磁场理论研究与计算、电机瞬变过程分析与计算、电机故障分析等，高级工程师。