一类非线性抛物型方程解的熄灭

万冬梅 宋益荣

（商丘职业技术学院，河南商丘476000）

一类非线性抛物型方程解的熄灭

万冬梅 宋益荣

（商丘职业技术学院，河南商丘476000）

非线性抛物型方程解的一个重要性质就是解的熄灭现象。它在实际生活中有很广泛的应用。近年来人们利用能量估计法，上下解的方法对非线性抛物型方程的解的熄灭进行了大量的研究。在这里受文献的启发，采用能量估计的方法，讨论了一类抛物型方程初边值问题解的渐进性态，得到了解在有限时间内解熄灭的条件。在此基础上给出了解的能量估计。

非线性抛物型方程；熄灭；初边值问题

1 引言

非线性抛物型方程解的一个重要性质就是解的熄灭现象。有着广泛的物理背景。再热的传导，化学反应，生物的粘弹性的扩散等方面，有着广泛的应用。黄瑜等（2004）讨论了方程的初边值问题，对解熄灭的充分必要条件作了详细的讨论。闫莉等（2006）则对已有的结果进行了推广。受启发这里考虑以下初边值问题

其中Ω是N维欧氏空间RN中的有界光滑区域，边界记为坠Ω，λ，β，γ，P是正整数，初值u0（x）不恒为，△表示Laplace算子。本文用‖·‖q表示Lq（Ω）中的范数，|Ω|表示Ω的测度。

定义存在T0∈（0，∞），对问题（1）的解u（x，t）成立

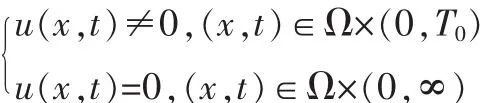
则称解u（x，t）在有限时间内熄灭。本文的主要结果是：

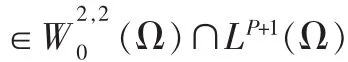
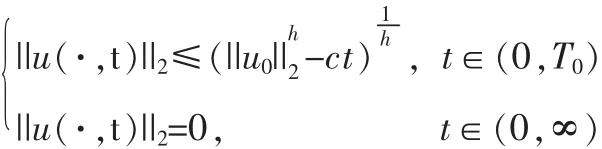
2 定理的证明

证：在方程（1）的两边同时乘以u后在Ω上积分得

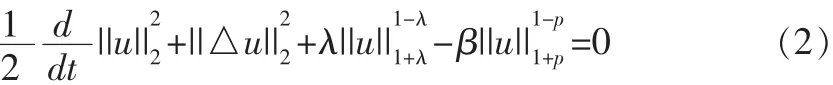
由Holder不等式

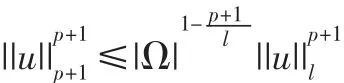
其中l>p+1待定。

由Gargliardo-Nirenderg不等式

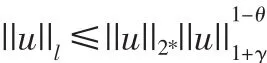
有Young不等式和Sobolev嵌入不等式，有

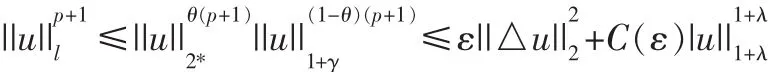
其中

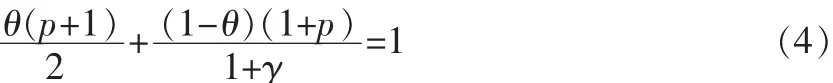
常数C与u（x，t）无关。为方便起见，我们把这类参数都以C表示。由Gargliardo-Nirenderg不等式可得

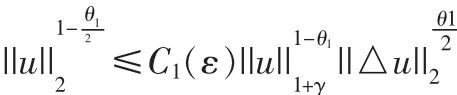
由Holder不等式，对ε>0，存在C1（ε）成立

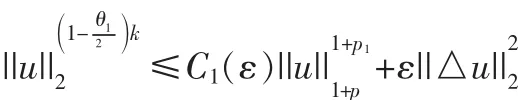
其中

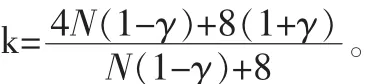
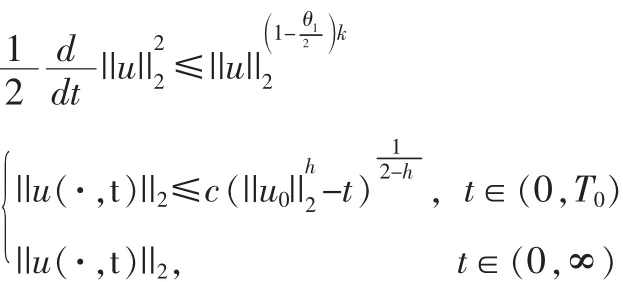
证毕。

[1]黄瑜，李刚于勇.一类具有非线性迁移顶的拟线性抛物方程解的熄灭[J].南京气象学院学报，2004，（5）：63-66.

[2]陈松林.一类反应扩散方程解熄灭现象[J].应用数学和力学，2001，（22）：1217-1220.

[3]闫莉，穆春来.一类非线性抛物方程解的熄灭[J].四川大学学报（自然科学版），2006，（3）：514-516.

[4]顾永耕.抛物型方程解的熄灭的充要条件[J].数学学报，1994，（1）：73-79.

［责任编辑：熊荣生］

Quenching of the Solution on a Type of Nonlinear Parabolic Equation

WAN Dong-mei SONG Yi-rong
（Shangqiu Vocational and Technical College，Shangqiu 476000，China）

The quenching phenomenon of solution is one of the important qualities of nonlinear parabolic partial differential equation.It is applied widely in our life.In recent studies on the quenching of a solution for the nonlinear parabolic equation，different approaches like energy estimation are adopted.This paper discusses initial boundary value problem for the parabolic equation，with the energy estimation method as its main approach.The conditions under which the solution is quenched will be given in this paper.Also，the energy estimation for the above equations will be concluded.

nonlinear parabolic equation；quenching；initial boundary value problem

O175.29文献标志码：A文章编号：1671-9565（2010）03-027-02

2010-06-25

万冬梅（1972-），女，河南商丘人，商丘职业技术学院讲师，主要从事基础数学方面研究；

宋益荣（1971-），女，河南商丘人，商丘职业技术学院讲师，主要从事基础数学教学方面研究。