引导有效数学实践活动 培养学生思维能力

闵丽云

《数学课程标准(试验稿)》将实践活动作为数学学习的一个重要组成部分。其要求是:数学教学活动必须建立在学生的认知发展水平和已有知识经验基础之上,教师向学生提供充分从事学习活动的机会,帮助他们在自主探索和合作交流的过程中真正理解和掌握基本的数学知识和技能、数学思想和方法,获得广泛的数学活动经验。因此,教学时应结合学生的实际经验和已有知识设计富有情趣和意义的活动,让学生通过参加有效的教学实践活动,发现、理解和掌握知识,使思维能力和智力水平得到提高。下面我结合自己的实践与探索,谈谈如何引导学生进行有效的数学实践活动。

一、挖掘课本实践性活动的素材,激发学生实践活动的动机

初中数学是一门实践性科学,许多数学问题的得出,数学规律的发现得出都离不开动手实践。教师要充分挖掘可以探索的内容,灵活运用这些材料,创设可以开展实践活动的数学问题,使学生产生“动”的愿望,体验成功的喜悦。课本是学生乐于探索研究的“活”教材。例如:在讲授判定三角形全等的边角边公里时,我先让每个学生利用直尺和量角器在白纸上作一个△ABC,使∠B=40°,AB=3cm,BC=5cm,并用剪刀剪下此三角形,然后与其他同学所作三角形进行叠放在一起,看看能否重合,这时学生们会发现是能够重合的。接下来,让学生改变角度和长度大小再做三角形,剪三角形并对照,这样学生自然会发现每次所作三角形都能够完全重合。此时,教师启发学生总结出:如果两个三角形有两边和夹角对应相等,那么这两个三角形全等,即“边角边”公理。通过同学们的动手操作,既活跃了课堂气氛,激发了学生的学习兴趣,又使抽象的数学知识蕴于简单实验之中,使学生易于接受新知识,促进学生认知理解。

二、借助数学互动实践,引导学生加深对概念、性质的理解

数学概念、性质、定理等具有高度的抽象性和概括性,如果让学生直接理解,肯定会存在很大困难,列夫托尔斯泰曾说:“知识,只有当它靠积极的思维得来,而不是凭记忆得来的时候,才是真正的知识。”因此,新的课程标准要求教师在概念教学中注重知识的生成,引导学生从已有的知识背景和活动经验出发,提供操作、思考与交流的机会,让学生经历观察、实验、猜测、推理、交流与反思等过程,进而在增加感性认识的基础上,帮助学生形成数学概念。

如在讲“有理数的乘方”时,我从“折纸问题”开展教学,提出问题:“有一张厚度为0.1mm的纸,将它们对折一次,厚度为0.1×2mm,对折10次,厚度是多少毫米?对折20次厚度是多少?”在学生动手折叠纸张进行计算厚度的过程中,大部分学生计算对折10次时的厚度就显得很为难,他们表现出渴求寻找一种简便的或新的运算途径的欲望,此时,教师适时引出“乘方”的概念,用乘方表示算式0.1×220比用20个连乘简洁明了得多,其值为104.8576米,比30层楼(每层3米)还要高。学生通过这种主动参与教学活动,加深了对“乘方”概念的理解,从而提高了教学效果。

三、创设实验型思维,培养学生自主探索知识的能力

亚里士多德讲过:“思维是从疑问和惊奇开始。”激发学生的好奇心和求知欲望,是培养学生创新精神与实践能力的推动力。因此,在数学课堂教学中,教师应创设出各种具有问题情景实践活动环节,激发学生的学习兴趣,使学生心里产生一种强烈的求知欲,为学生进行自主探索创造良好的条件。

如讲全等这章时,创设这样一个情境:已知一个三角形的两边长分别是1cm和2cm一个内角为40°①请你借助下图画出一个满足题设条件的三角形;②你是否还能画出既满足题设条件,又与(1)中所画的三角形不全等的三角形?若能,请你在下图画这样的三角形;若不能,请说明理由;③如果将题设条件改为“三角形的两条边长分别是3cm和4cm,一个内角为40°,”那么满足这一条件,且彼此不全等的三角形共有___________个。

通过这个例题,可以说明当两边一角不一定全等。

教师在教学中应该使学生既长知识又长智慧,学生思维能力的发展,同样也可以在实践活动中逐渐培养。学生通过参加教学实践活动,可以把思维和实践活动有机地结合起来,使他们的思维得到发展。

四、借助有效的数学实验手段,培养学生不断探索精神

数学实验可以帮助学生从本质上去理解数学,在实验中从多方面、多角度去联想、思考、探索,掌握数学知识。在数学教学中,教师通过创设互动实验,鼓励学生大胆尝试,积极参与,使不同基础的学生在互动实验过程中都有所收获。

如苏科版圆周角一节的教学中,就可以这样设计:

请同学画出如图1所示的图形,进行实验。

(1)测算∠AOB和∠ACB的度数。点C在圆周上运动,观察∠ACB的变化及与∠AOB的关系;

(2)改变∠AOB的大小,重复以上实验,看(1)中的结论是否仍然成立?

(3)通过以上实验,你能得到什么结论?你能证明你的结论吗?

通过实验、观察,学生很容易发现:同一条弧所对的圆周角等于它所对的圆心角的一半。

此时继续用实验引导,让点C在圆周上反复运动,学生观察、思考∠ACB与∠AOB还有其他的位置情况吗?经过讨论、交流,学生发现图(2)仅仅是∠ACB与∠AOB一种特殊的位置关系。学生试着对结论进行证明,从而让学生体会到这样的结论才是可信的。

本案例中,让学生经历了“实验发现——归纳猜想——证明结论”整个过程,学生收获的将不仅仅是知识,更多的是学习的兴趣和能力的提高。

五、设计开放性的数学实践活动,让学生在实践中提高创新思维能力

数学开放题正是凭着其开放性、实践性、创新性,在课改中努力体现新理念,实现新目标。对学生的学习和发展是具有导向性的,促进了数学教育的开放化和个性化,从发现问题和解决问题中培养学生的创新精神和实践能力。

适当拓展课本例习题,让学生在开放性与探索性活动中提高思维活动水平,开放性试题能给每一位学生提供用自己掌握的知识、熟悉的方式去表达对问题的理解的机会,有利于培养学生发散思维的水平,数学实践能力和探索能力。

如图1,正三角形ABC中,在AB、AC边上分别取点M、N,使BM=AN,连接BN、CM,发现BN=CM,且∠NOC=60°。请证明:∠CNO=60°。

(2)如图2,正方形ABCD中,在AB、BC边上分别取点M、N,使AM=BN,连接AN、DM,那么AN=________,且∠DON=

度。

(3)如图3,正五边形ABCDE中,在AB、BC边上分别取点M、N,使AM=BN,连接AN、EM,那么AN=________,且∠EON=________度。

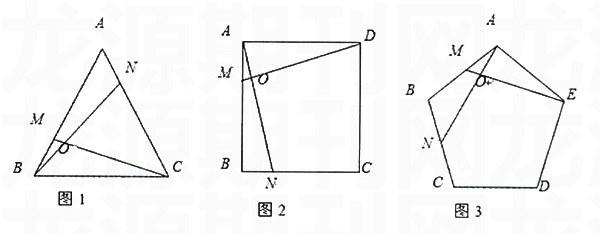
(4)在正n边形中,对相邻的三边实施同样的操作过程,也会有类似的结论。请大胆猜测,用一句话概括你的发现:________。

通过设计类似上面不同类型开放题的研究,可以有效地培养学生的自主探究能力、分析和解决问题的能力。当学生对开放题的基本知识和各种类型了解后,教师要在此基础上对各种类型的开放题解答方法进行归类总结,以达到举一反三、触类旁通之效。在教师指导下鼓励学生大胆实践,有效提高学生的探究能力。

有效的数学实践性活动,就是给学生一个研究、探索和展示智慧的空间,是让学生理解数学知识的教学活动,注重亲身实践,主动参与,使学生学会知识的同时,学会怎样学习,学会发现知识;能逐步养成学生认真观察,勤于思考的习惯,培养学生善于发现问题,提出问题,敢于解决问题,勇于探索的精神,培养了学生的创造精神与实践能力。