声波在二维固/流声子晶体中的禁带特性研究*
高国钦 马守林 金 峰 金东范 卢天健†
1)(西安交通大学机械学院,西安710049)
2)(西安交通大学强度与振动教育部重点实验室,西安 710049)
声波在二维固/流声子晶体中的禁带特性研究*
高国钦1)马守林1)金 峰2)金东范2)卢天健2)†
1)(西安交通大学机械学院,西安710049)
2)(西安交通大学强度与振动教育部重点实验室,西安 710049)
(2007年11月7日收到;2008年4月28日收到修改稿)
采用时域有限差分法(FDTD),分析了声波在二维四方点阵铝/空气组合声子晶体中的禁带特性,并利用实验测试验证了理论分析的正确性.在此基础上研究了两种不同声阻抗率比固(实心圆柱和空心圆管)/流系统声子晶体的禁带特性.对于实心圆柱体,分析了有限尺寸结构声子晶体在传播方向上的层数对声波传播特性的影响,得到了这两种系统在不同填充率下取得最大声波禁带宽度所需的最少层数.同时指出,在低声阻抗率比条件下,对于空心圆管填充物,通过选取适当的半径比,可以获得比实心柱体更宽的方向带隙.
声子晶体,时域有限差分法,禁带,声阻抗率比
PACC:4320,4335,6320,6780C
1.引言
弹性波特别是声波在声子晶体中的传播特性研究受到了广泛关注[1—25].当声波通过声子晶体时,会产生声子带隙,即声波在一定频率范围内(即当声波波长与结构的晶格常数可比时)的传播被抑制或禁止,该频率范围被称为声波禁带.声子晶体的这种禁带特性使得其在减振、降噪、声学器件等领域有着潜在的广阔应用前景.
作为一种新型功能材料,声子晶体通常由周期性排列在基体材料中的散射体复合而成,按其微结构可分为一维[1]、二维[2,3]和三维[4,5].对于二维结构,散射体排列的拓扑结构可以是三角形、四边行、六边形,或者是更复杂形状的周期性排列;散射体也可以具有不同的截面形状[6,7].与此同时,散射体和基体材料的组合也具有多样性,可以是固(体)/固(体)[2,3]、流(体)/流(体)[8]、固(体)/流(体)[9—13]等不同的组合形式.在这些组合中,固/流组合,特别是固/气(体)组合,由于散射体和基体的材料参数存在巨大的差异,易于禁带的产生.同时,流体材料的纵波速度通常小于固体中的纵波速度,产生的禁带频率相对较低,因而有利于声子晶体在可听频率范围的应用.
目前应用于声子晶体弹性波禁带的计算方法主要有平面波展开法(PWE)[2,3],时域有限差分法(FDTD)[14]和多重散射法(MST)[15]等.PWE应用比较广泛,计算实施相对简单,但是这种方法只能计算结构的能带关系,不能计算有限结构的透射和反射等特点,同时也很难获得禁带以外的传播特性,在解决流/固耦合问题上也存在缺陷.MST方法推导过程比较复杂,目前主要应用于三维球形和二维圆柱形散射体的禁带分析.而FDTD方法则可以有效地解决上述两种方法的缺陷与不足,已被广泛应用于有限结构声波禁带和声波导[16]以及负折射[17]等现象的研究中.
对于二维固/流声子晶体系统的研究,已经取得了一定的进展.1995年Martinez-Sala等人对西班牙马德里市名为“自由旋律”的雕像进行了测试,第一次从实验的角度证实了固/气系统声波禁带的存在[9].随后,Kushwaha发展了平面波展开法来计算这种高声阻抗率比结构的禁带特性[10],理论分析结果与实验测试值符合良好.随后几年,研究主要集中在无限结构声子晶体方面,对于禁带特性的研究也主要集中在改变结构的参数上,即改变散射体的截面形状(圆形、正三角形、方形、正六边形、正八边形等)、不同形状的旋转效应以及散射体不同的拓扑结构(四方排列,正三角排列,正六角排列等)[6,7,11,12].但是,在实际应用中,声子晶体的结构有限,而有关结构尺寸对声波禁带影响的研究则相对较少. Vasseur等人[18]用FDTD方法研究了两种不同声阻抗率比系统的禁带特性,对于高声阻抗率比系统,空管结构与实心柱体的传输特性没有显著区别,而对于低声阻抗率比系统则存在很大差异.但是空管半径比的具体影响还未被考虑.
针对两种不同声阻抗率比二维四方排列的固/流组合有限结构声子晶体的声波禁带特性,本文运用FDTD方法开展了理论和实验研究,分析了两种不同声阻抗率比固/流声子晶体的声波禁带特性,详细讨论了包括材料特性差异、传播方向上的层数以及管子半径比等因素对声波禁带特性的影响.
2.模型描述
二维固/流组合声子晶体通常是由在XY平面上周期性排列且在Z方向上无限长的散射体和基体材料组成的.图1为典型的二维四方排列声子晶体的横截面图,黑色部分为插入流体基体中的散射体,晶格常数为a.本文考虑X方向无限周期性排列、Y方向有限周期排列的系统.声波的传播方向平行于X-Y平面,Y方向对应于布里渊区的ГX方向,45°斜入射方向对应于ГM方向.两个方向获得的禁带叠加部分为完全禁带区域,即不管声波从哪个方向入射,完全禁带内的声波都不能通过声子晶体.
本文主要考虑实心圆柱体(半径为r)和空心圆管(内半径为ri,外半径为ro)两种填充物,对应的填充率分别为及两种不同声阻抗率比(声阻抗率Z=ρcl)系统声波的禁带特性:高声阻抗率比(铝/空气),低声阻抗率比(铝/水).表1给出了相关的材料参数.
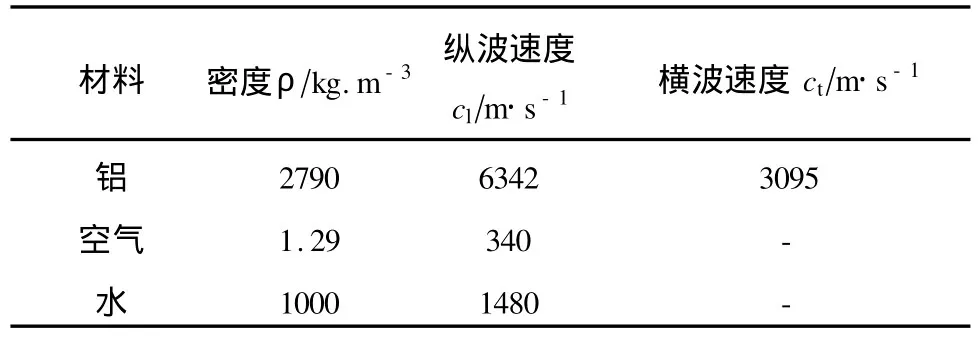
表1 材料参数
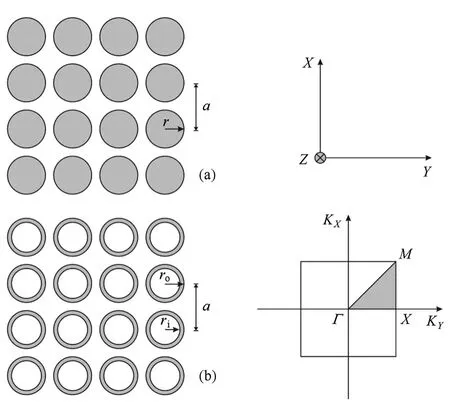
图1 四方排列在流体基体中的二维声子晶体的部分截面图以及相应的第一布里渊区 (a)散射体为实心柱体;(b)散射体为空心管
3.数值计算方法——时域有限差分法
时域有限差分法(FDTD)是基于对偏微分波动方程进行离散化处理的数值计算方法,即通过对时间和空间的离散将偏微分方程转化为差分方程,然后数值求解波传播过程中各个离散点上的所有参数与时间之间的函数关系.
3.1.控制方程
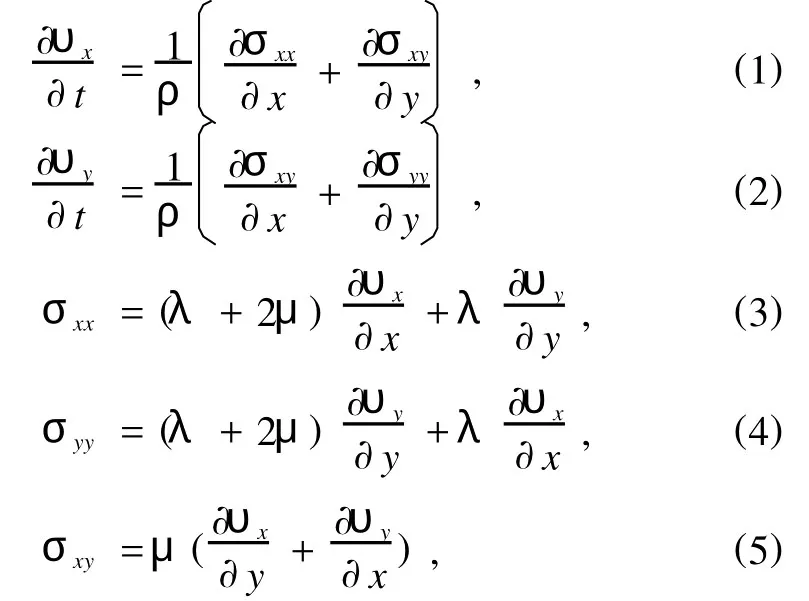
二维各向同性介质中声波的波动方程为[19]其中(υx,υy)为速度矢量,(σxx,σyy,σxy)为应力分量.对应于如图1所示的周期性系统,材料参数密度ρ和拉梅常数(λ,μ)皆为位置的周期性函数,其中λ分别为材料的纵波和横波速度,后者对应于流体时的值为0.文献[26]指出当黏性层厚度δ(δ=(2η/ρ ω)1/2,其中η为切变黏滞系数,ρ为流体密度,ω为圆频率)与复合材料的晶格常数可比的时候,黏滞作用不可忽略.然而,即使对于水下系统,黏滞力发挥作用时对应的晶格尺寸至少要小于0.5 mm(对应1 Hz),空气中则更小.目前研究的禁带通常在千赫兹以上,黏性层的厚度与晶格常数相比要小几个数量级,也就是说黏滞作用对于禁带特性的影响较小,可以忽略.
3.2.波动方程的离散化
将波动方程在空间和时间域上进行离散[19,24,25,27],空间步长取为Δx和Δy,时间步长取为Δt.对空间域采用中心差分
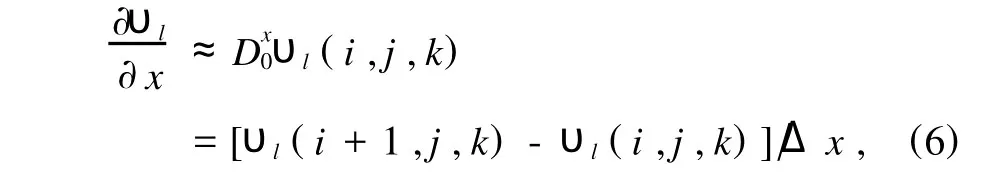
对时间域采用前向差分
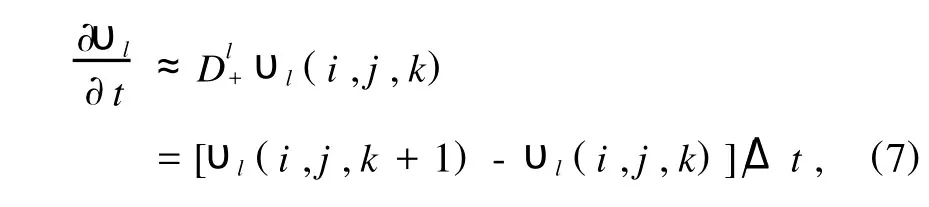
其中l=x,y.
引入半时间层k+1/2和半空间层i+1/2,j+1/2,采用正交网格将在空间和时间上交错配置,得到υx,σxx的差分格式如下:
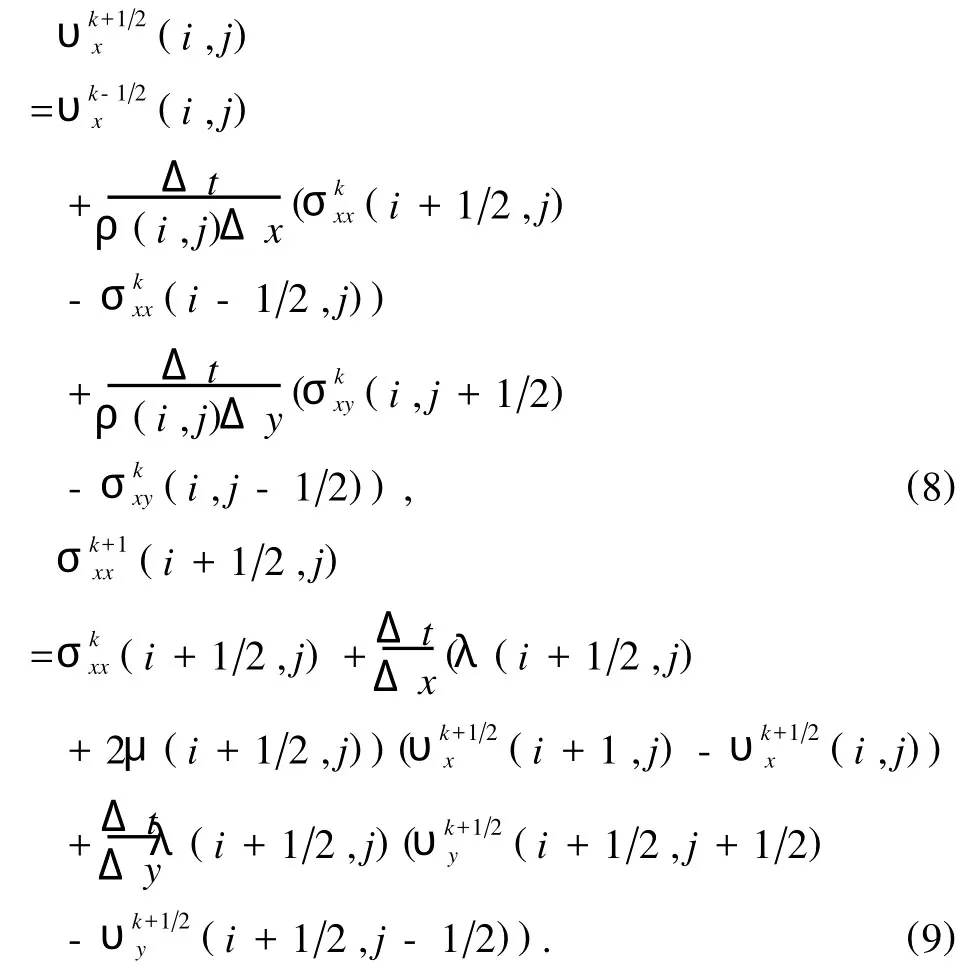
其他参数有类似的表达式.通过给定的初始激励,差分递推以后,可得到任意时刻任意位置的振动参数随时间的变化关系.
在上述计算中,为了确保算法的稳定性,采用如下的稳定性判据[14]:
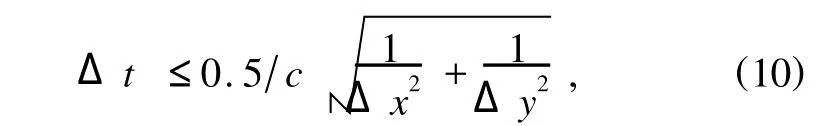
3.3.边界条件
实际求解过程必须限定在一个有限的空间区域之内,所以应当采用适当的边界条件来减少这种人为边界条件的影响.对于X方向无限周期排列的计算元可以根据布洛赫定理采用周期性边界条件[14],以减少计算时间;Y方向有限周期排列计算元如果不加吸收边界条件的话,就会造成波反射,影响计算结果.目前采用的吸收边界条件有多种,本文采用最普遍也最简单的一阶Mur吸收边界条件[28].
3.4.传输系数计算
为了计算传输系数,在计算区域的一端y=0平面赋予冲击激励(纵波速度激励),在区域的另一端得到纵波质点速度随时间的变化关系,然后用傅里叶变换转化为频域信号υy(ω).运用同样的方法,可得到同一位置上没有声子晶体样品时的初始激励频域信号Iy(ω).反复的计算过程表明,X方向质点速度分量相对于Y方向的质点速度分量相差几个数量级,因此在计算传输系数时,可以忽略不计.传输系数的计算采用下式:
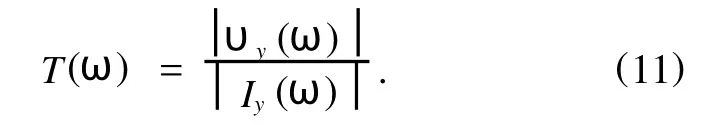
4.实验分析
4.1.实验设置
为了验证理论计算的正确性,制备了一个40× 6四方排列在空气中的空心铝管样品并对其进行测试:铝管外半径7 mm,内半径5.5 mm,管长500 mm,晶格常数为17 mm,填充率为0.2038,材料参数见表1.
所有实验在专业消声室中进行以消除背景噪声的干扰.图2为整个实验装置的示意图,信号发生器(B&K1027)产生的白噪声信号经功率放大器(B&K 2718)、扬声器(Alpine SPS-170A)、试件、传入声级计(B&K2230),最后输入频谱分析仪(HP 35670A).扬声器和传感器位置由L1和L2确定,其中L1=500 mm,L2=250 mm.传输系数测试原理与上述FDTD方法相同.
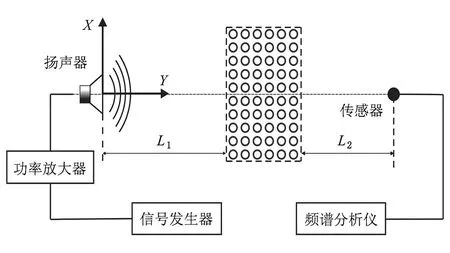
图2 实验装置示意图
4.2.实验测试与理论预测比较
图3给出了铝管/空气组合声子晶体沿ГX方向的传输系数的理论计算和实验测试曲线.理论计算取空间步长Δx=Δy=a/60,时间步长5.6412 ns.理论预测的ГX方向禁带为5.9—13.1 kHz;为了获得完全禁带,同时也计算了ГM方向的禁带特性,获得的完全禁带为9.7—13.1 kHz.在完全禁带区域,实验测试结果与理论计算值符合良好,两者的传输系数都小于2%(图3).在非完全禁带区域,由于激励声源不是平面波声源,到达样品的声波并非都是垂直入射,还包含斜入射成分,所以在禁带前段存在一定的误差.同时,实际测量中不可能将管子取成无限长以及X方向无限周期排列,这就造成了禁带以外的区域特别是低频部分不可避免地出现绕射,使得测量值出现大于1的现象.尽管如此,FDTD算法在预测禁带的范围内仍与实验结果符合良好.
5.两种不同声阻抗率比系统的声波禁带特性
5.1.纵波声场的质点速度比较
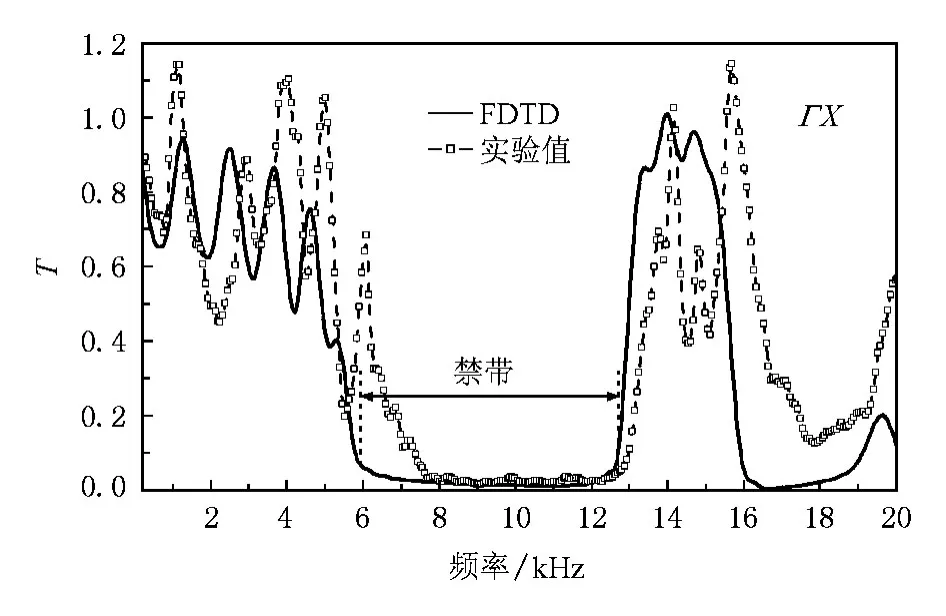
图3 铝管/空气声子晶体沿ГX方向传输系数曲线理论值和实验结果比较
文献[18]指出:在高声阻抗率比系统中,管状填充物跟柱状填充物的传输系数曲线没有区别,而低声阻抗率比系统则存在较大差异.图4给出了采用FDTD方法获得的两种不同声阻抗率比系统在某一时刻沿ГX方向的纵波声场的质点速度场(声阻抗率Z=ρcl);为了计算方便,选取3×3计算元.图中上半部为实心铝柱,下半部为空心铝管.从图4(a)可以看出,由于铝的声阻抗率远大于空气,所以当声波从空气入射到铝管时,在界面处发生全反射,导致声波不能在管中传播,所以实心柱体和空心管有相同的散射场.入射波与反射波的干涉作用形成禁带.高声阻抗率比系统的这一特性对于实际应用中实现材料的轻质化具有重大意义.图4(b)描述了低声阻抗率比系统的散射特性:当声波从水入射到铝时,在界面处一部分发生反射,一部分进入固体.对于管状填充物,在管子的内表面和外表面都会发生反射,这势必影响散射场特性,所以两种填充物的传输系数曲线存在很大的不同.从图4(b)的上半部分和下半部分可以很清晰地区分实心和空心管子的形状,这是在高声阻抗率比系统中观察不到的现象.
由上述可知,在低声阻抗率比系统中,管子厚度对于传输系数曲线有很大影响;同时也反映出传统的PWE方法在计算这种系统时的缺陷,即假设固体刚性,声波不能穿透散射体,只能在基体中传播[13].需要指出的是,上述分析只是定性地给出了材料的物理特性差异的影响,而在工程实践中很难给出高声阻抗率比和低声阻抗率比系统的具体界限.
5.2.声子晶体在传播方向上层数的影响

图4 两种不同声阻抗率比系统某一时刻沿ГX方向的纵波声场质点速度(上图为实心柱体,下图为空管) (a)铝/空气组合; (b)铝/水组合
实际应用中声子晶体不可能无限周期排列,因此研究其在声波传播方向上的层数影响,对于计算的收敛性问题和声子晶体的尺寸设计具有重要意义.图5给出了水下四方排列实心铝柱声子晶体沿ГX方向(以下没有特殊说明,均为ГX方向)的传输系数T随层数N变化的计算结果;晶格常数a= 17 mm,半径r=7mm,填充率F=0.5327.计算结果表明,随着层数的增加,禁带中的传输系数值逐渐减小且禁带边界逐渐明显.N=8时,禁带已经有比较明显的边界和传输系数值(小于2%),而且N =8和N=16时的传输系数曲线没有太大差异.因此,在选定的填充率(F=0.5327)下,8层已经能基本满足计算需求,即8层为这种填充率下实现声波最大禁带所需的最小层数Nmin.
不同填充率下,在两种不同声阻抗率比系统中实现最大禁带计算所需的最小层数Nmin如图6所示;计算时取a=17 mm,ro=7mm,ri=5 mm.填充率小于0.3时,禁带宽度很小,因此图中只计算了填充率大于0.25的情况.结果表明,随着填充率的增加,所需的最小层数降低,这和建筑学中的质量作用定律[29]相一致.把声子晶体模型抽象为一道隔墙,对于一定频率的声波,当单位面积的质量增加时,隔墙的隔声能力相应提高:因此,在相同的隔声量需求条件下,可以减少墙体的厚度.
对于现代企业而言,固定资产投资行为管理信息化不仅仅是一个目标,更是一个过程,是一个不断完善、不断优化的过程,不仅仅是采用一种信息技术或一个软件系统,更重要的是管理观念的革新。一般而言,现代企业固定资产投资行为管理信息化的建设目标应包括这几个内容:
相同填充率下,低声阻抗率比系统比高声阻抗率比系统需要更多的层数来实现最大禁带.由方程(1)—(5)可以看出,在固/流界面,高声阻抗率比系统的纵波速度衰减要比低声阻抗率比系统来得慢,这样反射场在与入射场叠加的时候就需要更多的反射部分来抵消入射场,即需要更多的层数.
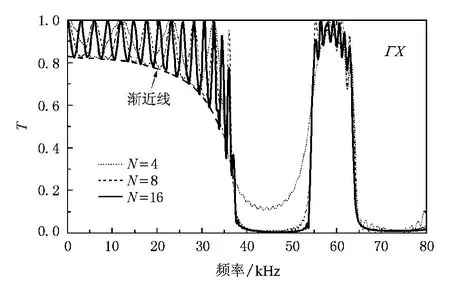
图5 实心铝柱/水声子晶体传输系数曲线随层数的变化
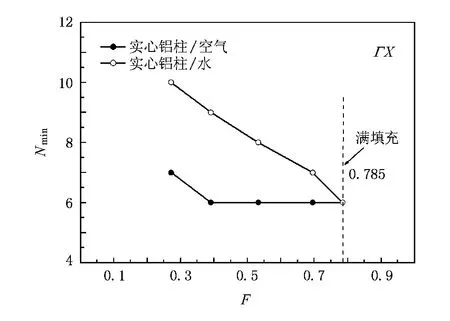
图6 两种不同声阻抗率比系统中,不同填充率下实现最大禁带所需的最少层数
从图5还可以发现,低于禁带频率的部分出现曲线摆动,摆动的峰值个数与所取的层数N相等,而图3给出的实验测试结果也有类似现象.这主要是由于反射分量随层数的增加而增加,从而改变了不同频率入射波与反射波的叠加特性.对于低声阻抗率比系统,N≤17时,峰值个数与N相等.这意味着实际应用中,17层已经基本满足实际需求,再增加一层所造成的反射分量非常小,不足以引起曲线的敏感波动.而对于高声阻抗率比系统,只有N≤6时,峰顶点才等于N.这些点的位置没有确定的规律,但是同一填充率下不同层数所对应的传输曲线的所有峰谷点都落在同一条曲线上,如图5所示.
5.3.圆管内外半径比对传输系数的影响
图4的结果表明,圆管的半径比对于高声阻抗率比系统的传输系数曲线没有影响,而对于低声阻抗率比系统其影响则非常大.图7描述了这种低声阻抗率比系统的传输系数曲线随半径比变化的关系;材料结构参数与图3一致.
图7(a)中,半径比缓慢增大,从0.429,0.471到0.500;可以看到第一禁带的下限基本不随半径比变化,而上限对半径比的变化非常敏感.随着半径比增大,第一禁带和第二禁带中的尖峰部分向左移动.这意味着选取适当的半径比,有可能使得中间的尖峰部分移到第一禁带的下限左边区域,使得第一禁带跟第二禁带合并,形成一个相对较宽的禁带.为了证实上述推论,计算了不同半径比对传输系数的影响;图7(b)描述了半径比等于0和0.571时的传输系数曲线,半径比为0.571时的禁带范围为38.5—68 kHz,而实心柱体(半径比等于0)的禁带范围为36.1—54.1kHz,宽度远远小于前者,禁带起始频率低于前者,同时合并后的禁带宽度要比未合并时的第一第二禁带宽度和小.当半径比大于0.571时,禁带宽度又逐渐减小(因篇幅限制,计算结果不在这里给出).所以0.571为获得最大禁带宽度的最优半径比.对于具有两层界面的空管结构,它的叠加场主要是由入射波跟两个界面的反射波组成.当晶格常数与外径固定,改变管子厚度,第二层界面的反射波相位随之改变.管子厚度对相位的这种调制作用影响了声波的叠加场特性.上述计算表明,0.571的半径比,最有利于两个反射波抵消入射波.
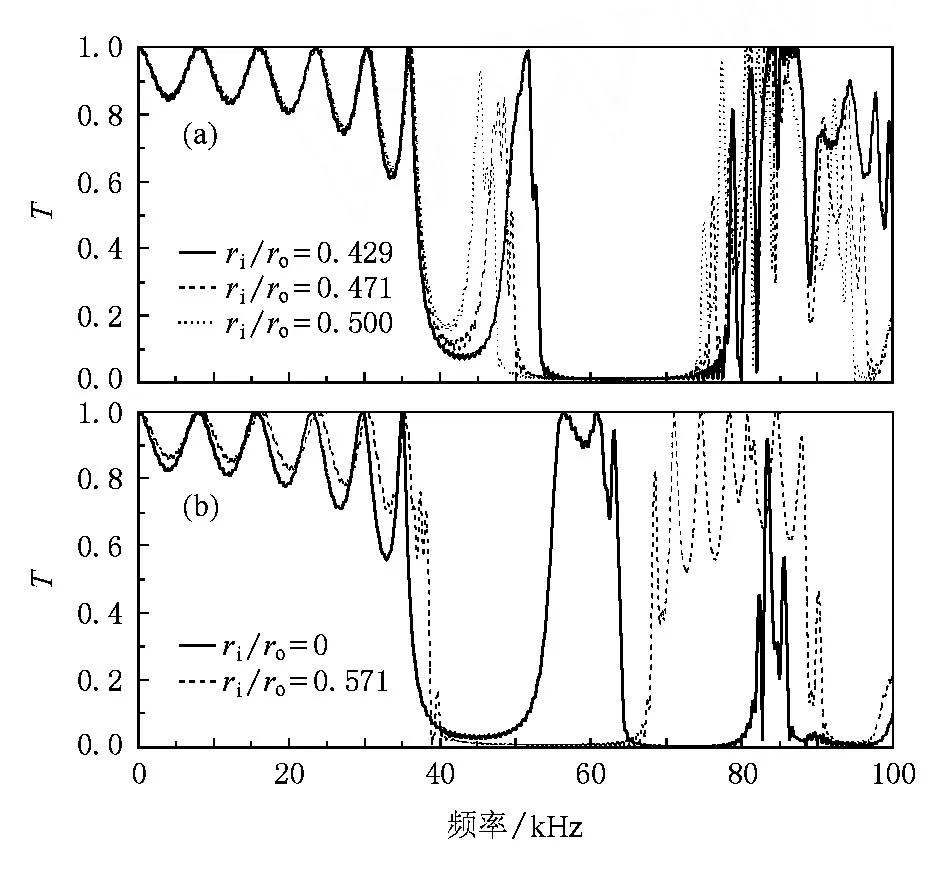
图7 铝管/水声子晶体传输系数T随管子半径比ri/ro变化的关系 (a)ri/ro=0.429,0.471,0.500;(b)ri/ro=0,0.571
由文献[12]可知,禁带宽度与晶格常数a成反比关系,所以可以定义无量纲化禁带宽度为ΔΩ=(Δf为禁带宽度).图8给出了实现最大禁带铝管/水系统与实心铝柱/水系统的无量纲化第一禁带宽度的对比.结果表明在外径填充率大于0.730或小于时,实心柱体是产生最宽禁带的理想结构:当外径填充率小于0.196时,虽然也能够实现禁带的合并,但是由于第一禁带和第二禁带宽度在低填充率下相对较小,合并以后增大的宽度小于禁带下限频率的增加量,所以整体禁带宽度要小于实心柱体结构;当外径填充率大于0.730时,对于实心柱体,虽然禁带宽度增大,但是禁带的位置向高频移动,第二禁带的起始频率已经大于90 kHz(低填充率下,实心柱体的第一、第二禁带都处在90 kHz以下),这意味着管子厚度引起的相位调制作用只有在特定频率范围才能起作用.而在中间区域,可以通过选取适当的空管内外半径比,得到比实心柱体更宽的禁带:在外径填充率等于0.53时,两者的宽度比达到最大,为1.64,这从增大禁带角度考虑,是非常可观的.同时,图9描述了不同外径填充率下最大禁带铝管/水系统对应的最优半径比,其中中间部分的最优半径比随外径填充率的增加近似线性减少.这一计算结果为水下管状声子晶体声波禁带的设计提供了依据.
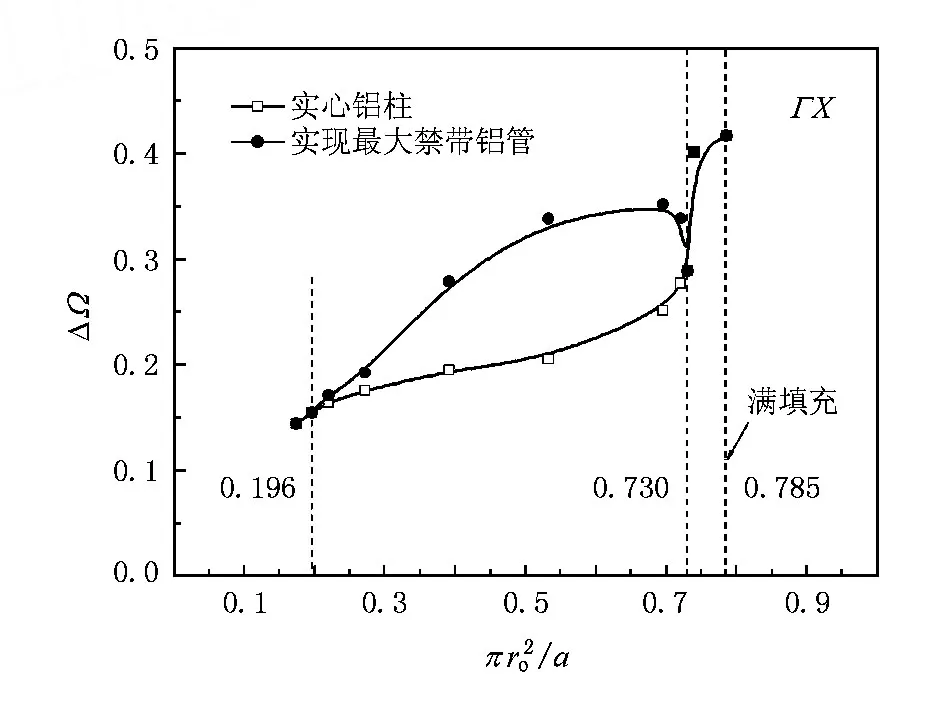
图8 实现最大禁带铝管/水系统与实心铝柱/水系统的无量纲化第一禁带宽度对比
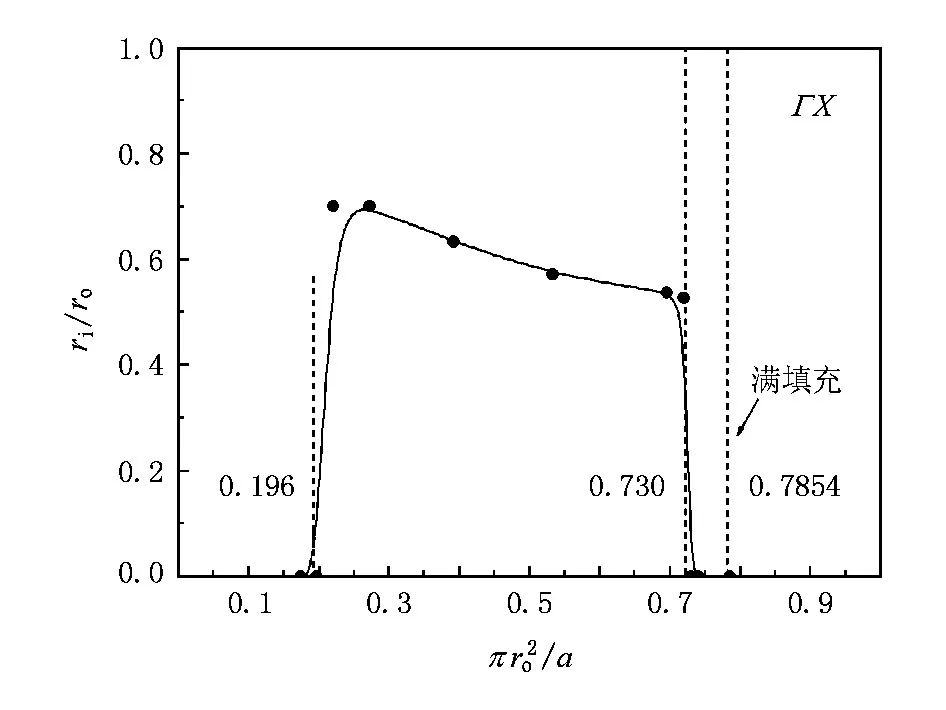
图9 不同外径填充率下对应的铝管/水系统最优半径比
空管最大禁带计算的结果对低声阻抗率比系统具有双重意义:首先,空管比实心柱体更轻,从节省耗材角度来讲更有利于实际应用;其次,只需把禁带的下限向高频移动一个很小的值,就可获得宽于实心柱体中所获得的禁带宽度的禁带.
6.结 论
本文着重研究了管子为填充物的二维四方排列固/流组合的声子晶体的声子禁带特性,应用时域有限差分法(FDTD)计算了有限层声子晶体的声传输系数,对铝管/空气组合的有限声子晶体实测禁带特性与计算结果相符.在此基础上,进一步研究了高和低声阻抗率比两种声子晶体系统中纵波散射声场的质点速度分布,沿声传播方向上声子晶体层数对传输系数的影响,层数与填充率的关系,以及内外管径对声传输系数的影响,得到如下结论:
1.高声阻抗率比系统比低声阻抗率比系统更易于产生禁带.
2.对于实心柱体填充物,低填充率系统需要比高填充率系统更多的层数以实现相同的最大禁带,这种现象在低声阻抗率比系统中表现得尤为明显.同时,同一填充率下,低声阻抗率比系统实现最大禁带需要的层数要比高声阻抗率比系统多.
3.对于空管填充物,管壁厚度对高声阻抗率比系统没有影响,但对于低声阻抗率比系统,选取适当的半径比,可以获得沿ГX方向比实心柱体更宽的禁带.
由于散射体与基体的材料物理特性差异大,固/流系统易于产生禁带.同时由于空心柱体易于内部流体的流动,可用于设计具有良好隔声性能的新型热交换器,或用于热交换器的泄漏噪声探测等.
[1]DowlingJ P 1992J.Acoust.Soc.Am.91 2539
[2]Sigalas M M,Economou E N 1993Solid State Commun.86 141
[3]Kushwaha M S,Halevi P,Djafari-Rouhani B 1993Phys.Rev. Lett.71 2022
[4]Kafesaki M,Sigalas M M,Economou E N 1995Solid State Commun.96 285
[5]Kushwaha M S,Djafari-Rouhani B 1996J.Appl.Phys.80 3191
[6]Zhong L H,Wu F G,Zhang X,Zhong HL,Zhong S 2005Phys. Lett.A 339 164
[7]Kuang W M,Hou ZL,Liu Y Y2004Phys.Lett.A 332 481
[8]Kushwaha M S,Halevi P 1996Appl.Phys.Lett.69 31
[9]Mártinez-Sala R,Sancho J,SánchezJ V,Llinares GVJ,Meseguer F 1995Nature(London)378 241
[10]Kushwaha M S 1997Appl.Phys.Lett.70 16
[11]Caballero D,Sanchez-Dehesa J,Rubio C,Mártinez-SalaR, Sánchez-P rez J V,Meseguer F,Llinares J 1999Phys.Rev.E 60 R6316
[12]Lai Y,Zhang X,Zhang Z 2002J.Appl.Phys.91 6191
[13]Kushwaha M S,Djafari-Rouhani B 1998J.Sound Vib.218 697
[14]Sigalas M M,Garcia N 2000J.Appl.Phys.87 3122
[15]Liu Z,Chan CT,Sheng P 2000Phys.Rev.B 62 2446
[16]Miyashita T 2005Measurement Science and Technology16 R47
[17]T orres M,Montero de Espinosa F R 2004Ultrasonics42 787
[18]Vasseur J O,Deymier P A,Khelif A,Lambin Ph,Djafari-Rouhanil B,Akjouj A,Dobrzynski L,Fettouhi N,Zemmouri J 2002Phys. Rev.E 65 056608
[19]Wang G,WenJ H,Han X Y,Zhao H G2003Acta Phys.Sin.52 1943(in Chinese)[王 刚、温激鸿、韩小云、赵宏刚2003物理学报52 1943]
[20]WenJ H,Wang G,Liu Y Z,Yu D L 2004Acta Phys.Sin.53 3384(in Chinese)[温激鸿、王 刚、刘耀宗、郁殿龙2004物理学报53 3384]
[21]Wang G,Wen J H,Liu YZ,Yu DL,Wen X S 2005Acta Phys. Sin.54 1247(in Chinese)[王 刚、温激鸿、刘耀宗、郁殿龙、温熙森2005物理学报54 1247]
[22]Wu F G,Liu Y Y2002Acta Phys.Sin.51 1434(in Chinese)[吴福根、刘有延2002物理学报51 1434]
[23]Qi GJ,Yang SL,Bai S X,Zhao X2003Acta Phys.Sin.52 668 (in Chinese)[齐共金、杨盛良、白书欣、赵 恂2003物理学报52 668]
[24]García-Pablos D,Sigalas M M,Montero de Espinosa F R,T orres M,Kafesaki M,Garc a N 2001Phys.Rev.Lett.84 4349
[25]Taflove A 1998The Finite-Difference Time-Domain Method(Boston: Artech House Press)
[26]Biot M A 1961J.Appl.Phys.33 1482
[27]Li D B 2005Computational Acoustics(Beijing:Science Press)(in Chinese)[李大宝2005计算声学(北京:科学出版社)]
[28]Mur G1981IEEE Trans.on Electromagnetic Compatibility23 377
[29]Du G H,Zhu Z M,G ong X F 2001The Basics of Acoustics (Nanjing:Nanjing University Press)(in Chinese)[杜功焕、朱哲民、龚秀芬2001声学基础(南京:南京大学出版社)]
PACC:4320,4335,6320,6780C
Acoustic band gaps in finite-sized two-dimensional solid/fluid phononic crystals*
Gao Guo-Qin1)Ma Shou-Lin1)Jin Feng2)K im T ong-Beum2)Lu Tian-Jian2)†
1)(School of Mechanical Engineering,Xi’an Jiaotong University,Xi’an 710049,China)
2)(MOE Key Laboratory for Strength and Vibration,Xi’an Jiaotong University,Xi’an 710049,China) (Received 7 November 2007;revised manuscript received 28 April 2008)
Acoustic band gaps in two-dimensional phononic crystal consisting of a finite-sized square array of parallel hollow aluminum cylinders in air are investigated with the finite difference time domain(FDTD)method.Experimental measurements were carried out to validate the theoretical predictions with excellent overall agreement achieved.The numerical method is used subsequently to study the band gap properties of phononic crystals composed of cylinder(both solid and hollow)/fluid systemsfor two different acoustic impedance ratios.For both types of system,the influence of the transverse size of the phononic crystal on the propagation properties is analyzed,and the minimum size to achieve the largest band gap width for different filling factors is determined.
phononic crystals,finite difference time domain,band gap,acoustic impedance ratio
*国家重点基础研究发展计划(973)项目(批准号:2006CB601202),国家自然科学基金(批准号:10632060),国家高技术研究发展计划(863) (批准号:2006AA03Z519),国家“111”引智计划项目(批准号:B06024)和教育部新世纪优秀人才支持计划(批准号:NCET-08-0429)资助的课题.
†E-mail:tjlu@mail.xjtu.edu.cn
*Project supported by the National Basic Research Programof China(Grant No.2006CB601202),the National Natural Science Foundationof China(Grant No.10632060),the National High Technology Research and Development Program of China(Grant No.2006AA03Z519),the National 111 Project (Grant No.B06024)and the Programfor New Century Excellent Talents in Universityies(Grant No.NCET-08-0429).
†E-mail:tjlu@mail.xjtu.edu.cn

