一种高效量子密钥分发系统主动相位补偿方法＊

王金东 秦晓娟 魏正军 刘小宝 廖常俊 刘颂豪

1)(华南师范大学信息光电子科技学院光子信息技术广东省高校重点实验室,广州 510006)

2)(广东广播电视大学工程技术系,广州 510091)

一种高效量子密钥分发系统主动相位补偿方法＊

王金东1)†秦晓娟2)魏正军1)刘小宝1)廖常俊1)刘颂豪1)

1)(华南师范大学信息光电子科技学院光子信息技术广东省高校重点实验室,广州 510006)

2)(广东广播电视大学工程技术系,广州 510091)

(2009年2月15日收到;2009年4月15日收到修改稿)

针对相位编码量子密钥分发系统相位漂移的实际问题,详细分析了目前解决相位漂移的主要方案,提出了一种“五点法”快速相位漂移参数的扫描方法.该方法只需对五个相位点进行单光子水平的相位扫描,即可得出满足精度要求的相位漂移参数.通过将该方法和其他两种主要相位补偿方法的对比分析,表明该方法可以在更短的扫描时间内有效得到量子密钥分发的相位漂移参数并对相位漂移进行实时补偿.该方法适用于目前常用的相位编码系统,为量子密码系统提供了一种有实际应用价值的主动相位补偿方案.

量子保密通信,相位编码,相位漂移,主动相位补偿

PACC:4250,0367,4230Q,9575K

1.引言

量子保密通信的想法是1983年由Stephen Wiesner最早提出.紧接着,量子保密通信的第一个协议于1984年由Bennett和Brassard提出[1],其实验可行性验证由Bennett和他的合作者们于1989年完成,实验结果在三年后发表[2].自此,量子保密通信在短短20多年时间里得到了迅猛发展[3—10],成为量子光学领域最接近实用化的应用之一.

相比偏振编码来说,光子信号在光纤中传输时其相位信息更易保持,因此绝大多数现有的光纤量子密码系统都采用相位编码方案[11,12].相位编码信息必须通过干涉检测的方法获得,所以干涉对比度直接决定了系统的误码率.从相干条件和干涉输出的结果来看,影响干涉对比度的因素主要有:光源的线宽和波长稳定性(频率相同);干涉检测环两路光子概率是否相同(强度相同);干涉叠加时偏振方向的符合程度(振动方向相同)以及单光子探测器的暗计数等.干涉叠加时相位差的稳定性保持以及密钥相位信息的精确加载虽然不影响整体条纹的干涉对比度,但是也在很大程度上影响了干涉输出的误码率.对于光纤双折射引起的偏振问题,已经可以采用著名的Faraday-Michelson(F-M)方案得到较好的解决[13],而相位稳定性的保持目前已经成为普遍关注的问题.干涉检测光纤环受到外界环境的影响会使得干涉输出的相位差不断发生变化,进而影响量子密钥相位编码信息的成功检测(误码率上升或根本不能检测).为了使得干涉输出能够正常检测密钥相位信息,目前针对环境引起的相位漂移主要有三种解决方案:

1)改进干涉系统的结构以适应地补偿相位漂移,如“plug-and-play”结构[11];

2)被动补偿,采用被动的方法降低外界环境对干涉系统的影响,如良好的隔温和避震措施等;

3)主动补偿,采用扫描的方式获取相位漂移的动态参数并进行实时补偿.

目前还没有看到理想的能够自适应补偿相位漂移的方案报道,其中“plug-and-play”结构虽然能够对光纤双折射和相位漂移进行较好的自补偿,但是该方案容易受到特洛伊木马攻击[5,14,15],并且双向结构降低了同等条件下的原始码率.

被动补偿方法主要有[16—19]:改进光纤环的制作材料和工艺以减小外界环境产生的影响,采取隔振措施以及对光纤环进行精密的温度控制以减小外界温度对相位漂移的影响,这些方法在一定程度上可以减小环境对相位漂移的影响或降低相位漂移的变化速度,但是无法从根本上消除相位漂移.

主动补偿方法可以通过实时调节光纤臂长的方法进行主动补偿[20,21],也可以实时扫描相位漂移参数并通过调节密钥信息编码相位调制器的调制电压进行主动补偿.对于相位漂移参数的扫描,一般有如下要求:

1)扫描精度满足系统误码率的要求;

2)扫描时间应尽量短,小于相位漂移的变化速度;

3)每次扫描过程之间的时间间隔应小于系统允许的相位漂移引起的误码率阈值的变化周期.

相位漂移参数的扫描可以采用在系统中引入强参考光来获取相位扫描参数[21,22],也可以在每脉冲平均光子数很小的单光子水平下进行[12,23,24].强参考光扫描方式增加了系统硬件部分的复杂度,带来不必要的干扰和引入新的误码,相比而言,基于单光子水平上的相位扫描模式具有较高的实用价值.但是单光子水平扫描的输出结果是光子计数,对于每一个相位扫描点,通过单次计数的结果无法获取相位漂移参数,需要在每个相位扫描点上进行足够多的计数累积,才可以得到相位漂移参数.同时,如果以较高的精度(较小的扫描步长)进行扫描,则每扫描一个周期花费的时间会比较长,可能在每次扫描结束后得到已经变化了的相位漂移参数,从而造成了较高的误码率.可见,在单光子水平上利用高效的扫描方式在尽量短的时间内得到相位漂移参数具有重要的实用价值,利用这种扫描方式不仅可以获得尽量精确的相位漂移参数,而且还可以提高系统的占空比,使得更多的光子能够用于密钥分发.

对于相位漂移的问题,除了探索可以自动补偿双折射效应和相位漂移的新方案以外,采用高效的方法对相位漂移进行实时补偿不失为一种解决实际问题的好办法.但是,单纯采用被动补偿和主动补偿都有某种不足:被动补偿不可能从本质上解决相位漂移问题,只能减小或减缓相位漂移,而主动补偿在相位漂移范围很大和飘移速度很快的情况下,其补偿效果得不到保证,所以应该首先利用被动补偿将相位漂移降低到一定的程度,然后采用高效的主动补偿算法进行适时补偿,才能保证系统脱离实验室环境的长期稳定性.

本文提出了一种“五点法”相位主动补偿方案,该方案只需要对五个相位点进行单光子水平的相位扫描,即可得出满足精度要求的相位漂移参数.整个扫描过程包括粗扫描和精扫描修正两个阶段.在第一阶段的粗扫描过程中,只需在一个调制周期内随机地选择三个扫描点进行扫描,通过干涉输出函数的计算即可获得系统相位漂移的粗扫描参数,然后在此基础上进行极值点精确扫描修正以获得满足精确度要求的精确相位漂移参数.此方法可以在更短时间内获得满足精度要求的实时相位漂移参数,进一步提高系统密钥分发占空比.

2.一种新的高效相位漂移参数扫描的方法

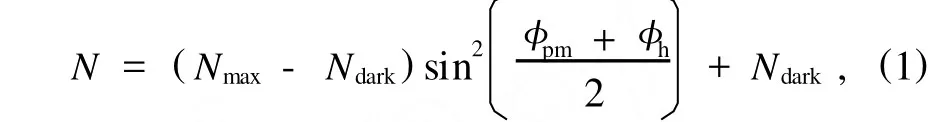
在量子密钥分发过程中,随着外界环境对光纤干涉环的影响,使得除了相位编码调制器的调制相位φpm以外,干涉环本身的附加相位φh也影响干涉输出的结果,干涉输出光子计数的表达式为其中,Nmax为干涉输出的最大光子计数值,Ndark为干涉输出的最小光子计数值,在不考虑光路中的其他因素(如干涉叠加时两路光子概率不等,偏振变化等因素)时等于单光子探测器的暗计数.干涉环的附加相位φh除了光纤环制作过程中长度差引起的固定相位差以外,还会由于外界环境的影响随时间不断发生变化,这种随机的相位变化使得干涉输出也会发生改变,进而影响相位编码信息的检测.由于相位不匹配造成的误码来源于两个方面:一是编码相位调制器调制电压的不准确造成的误码,二是相位漂移使得干涉相位差不稳定造成的误码.我们假设编码相位调制器可以准确地加载调制电压,那么干涉环相位漂移带来的误码可以表示为

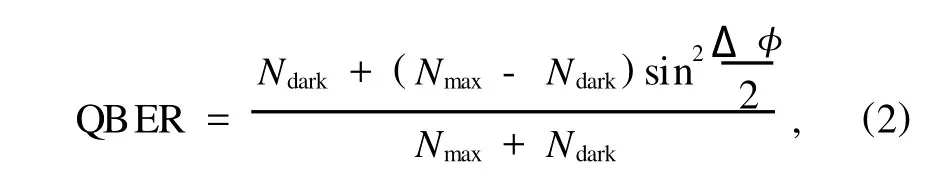
式中,误码率由计数周期内的最大计数、暗计数和相位漂移三部分决定,如果不考虑单光子计数器暗计数带来的误码率(令Ndark=0),那么上式变为

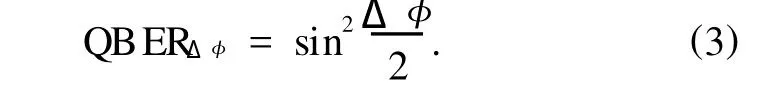
可见,必须对相位漂移进行控制来减小误码率以达到系统可以接受的程度,确保系统可以在高效补偿算法的作用下长期稳定工作.

我们注意到,在单光子水平的相位扫描方式中,每个扫描相位点进行足够多的光子计数输出累积后,扫描所得的干涉条纹能够较好的符合正余弦曲线,例如,在文献[12]中,每个相位扫描点等待1000个光子脉冲进行累积后,可以得到符合较好的正余弦曲线.根据干涉条纹的数学表达式(1)式我们可以看出,除了N和φpm可以通过实验获得以外,还有三个未知数需要通过扫描过程来确定:φh,Nmax和Ndark.既然在足够的光子计数累积后,实验结果可以很好地和理论曲线符合,那么在粗相位扫描的过程中,我们就不需要对相位点逐个进行扫描,我们只需要通过测量任选的三个相位点的光子计数输出,就可以通过(1)式得到相位漂移参数φh.在完成粗扫描后,再根据粗扫描的结果进行精确扫描修正,获得能够达到精度要求的相位漂移参数.

2.1.相位漂移参数的粗扫描

假设我们选择三个相位点进行扫描:φ1,φ2和 φ3,这三个调制相位对应的干涉输出光子计数的结果分别是N1,N2和N3,根据干涉条纹的数学表达式可以得到三个方程:

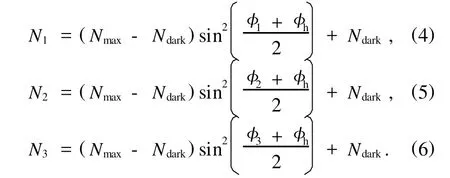
通过计算,可以得到由(4)式,(5)式和(6)式组成方程组的解析解为

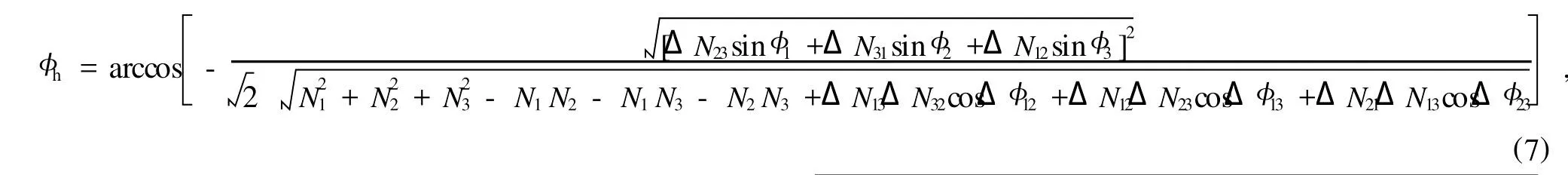
式中,ΔNij=Ni-Nj,表示所选相位点(φi和φj)对应光子计数结果(Ni和Nj)的差值,Δφij=φi-φj,表示所选相位点(φi和φj)的相位差.

通过(7)式,我们就可以选择三个相位粗扫描点来获得相位漂移参数φh,那么输出光子计数达到最小值时的密钥信息相位调制器的调制相位φmin可以用φh表示为φmin=2k′π-φh,而最大值所对应的调制相位φmax=φmin+k″π,式中k′和k″均为整数.

我们利用文献[12]和文献[24]中测量得到的光子计数干涉条纹进行这种粗扫描方法的实验数据验证.

在文献[12]中,我们任意选取三个测量点(V1, N1),(V2,N2)和(V3,N3),代入(7)式,可以得出相位漂移参数的粗扫描值为Vh=2.3V.在选取三个测量点时,我们对较符合理论曲线的数据点和偏差较大的数据点进行了计算结果的比较,发现不同数据点得出的粗相位扫描值的波动范围为Δ=0.2,对于粗扫描,这个精度是可以允许的.由粗扫描值,我们可以计算出现最小计数输出值的调制电压位置为Vmin=-0.72V,最大值为Vmax=2.48V,这个结果和文献[12]中的测量结果可以很好地符合,如图1(a)所示.

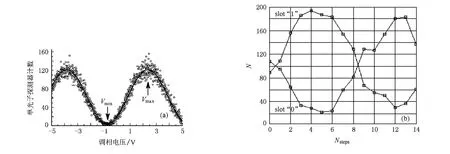
图1 粗相位扫描漂移参数结果验证数据图 (a)为文献[12]中逐点扫描的干涉条纹数据图;(b)为文献[24]中大步长粗扫描的光子计数数据图

用同样的方法,我们对文献[24]中的测量数据也进行了计算和比较,将文献中的15个扫描点分成5组,每组三个数据点,每组可以得到一个相位粗扫描参数为φh=1.526;1.659;1.952;1.752;1.876.根据这个结果,可以看到粗扫描相位漂移参数的波动范围最大为0.4,最大值出现的位置应在图1(b)中横坐标为3.7—4.6之间,和文献中的实验结果可以很好地符合,粗扫描精度在±12°之内.

2.2.相位漂移参数的精确扫描修正

通过第一阶段粗扫描的过程,可以获得相位漂移参数的粗扫描值,在第二个阶段,需要进行该参数的精确扫描修正.考虑到在干涉光子计数输出的最大值和最小值处进行小步长的精确扫描受到光子计数涨落的影响较大,很难提高相位漂移参数的获取精度,所以我们利用受光子计数输出涨落影响最小的两个相位点的干涉输出来对相位漂移参数进行精确扫描修正.

这两个精确扫描修正相位点的光子计数输出结果为

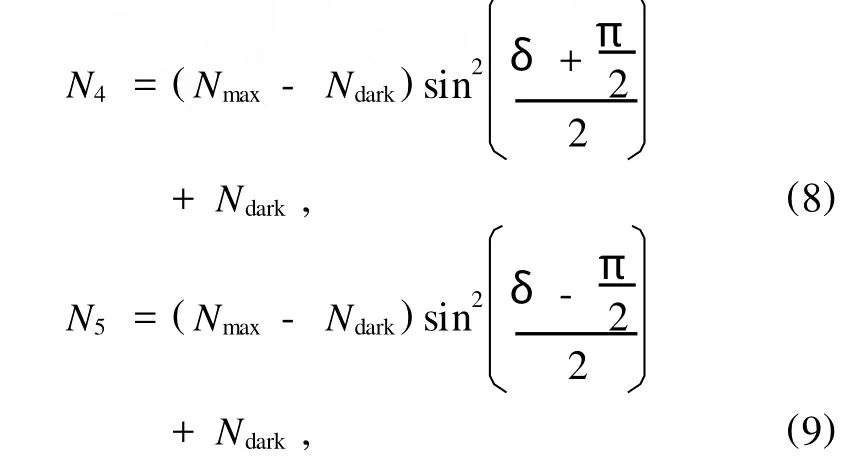
式中δ为相位漂移参数粗扫描值和精确值之间的差.将(8),(9)两式变换即可得到精确相位漂移修正参数

对由两个扫描点得出的修正参数进行平均,可以得到精确扫描修正参数为

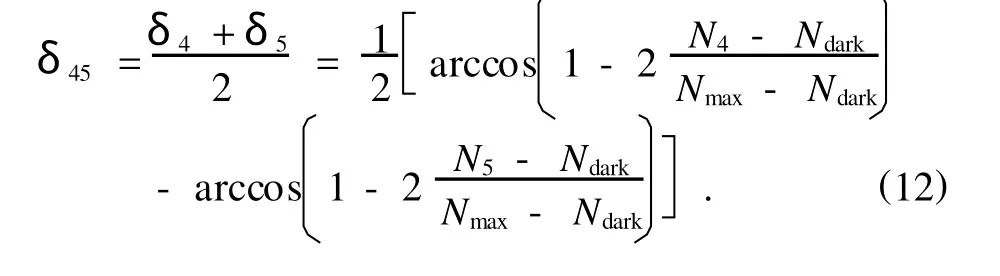
考虑到另外一个互补单光子探测器的输出,可以进一步取平均值得到最后的精确扫描修正参数[23,24]

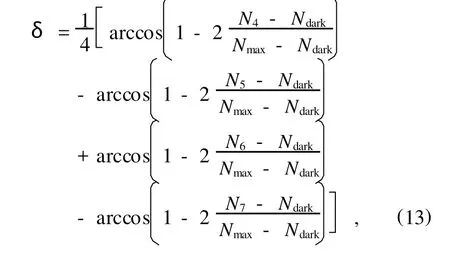
式中N6和N7为另外一路单光子探测器在两个精确扫描修正相位点的光子计数输出.在获得精确扫描修正参数以后,将第一步粗扫描中得出的相位漂移参数加上修正参数后即可得到修正后的相位漂移参数φh+δ.

2.3.相位漂移参数扫描精度的确定

利用文献[23]和文献[24]中的方法,可得扫描精度与总光子计数之间的关系:

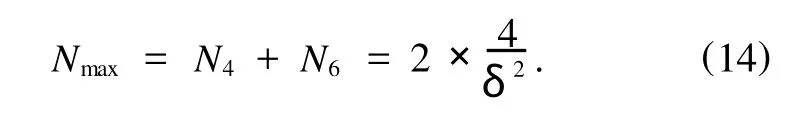
和文献[23]中的结果不同的是,在考虑两个精确扫描修正相位点的总计数的和为上述四个光子输出计数的总和,这四个光子计数输出的和应为2Nmax,所以可以得到四个光子计数值的总和与扫描精度之间的关系为

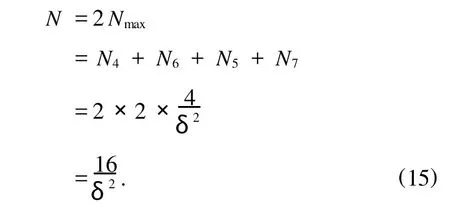
根据(15)式,我们可以得到扫描精度和四个光子计数输出总和之间的关系曲线,如图2所示.为了直观,图中的扫描精度以角度的单位给出.

从图2可以看出,随着扫描精度的不断提高,所需的计数值也会急剧上升,在同样的平均光子数和工作频率的条件下,所需的扫描时间也会急剧上升.例如,在工作频率1 MHz,平均光子数为0.1,单光子探测效率为10%以及不考虑暗计数的情况下,要达到10°的扫描精度,完成精确扫描修正需要的时间为52.6 ms,根据(3)式可以得到此时的相位精度造成的误码率为2.25×10-6,而要达到1°的扫描精度,完成精确扫描修正需要的时间则为5.26 s,而此时相位精度造成的误码率为6.25×10-8.

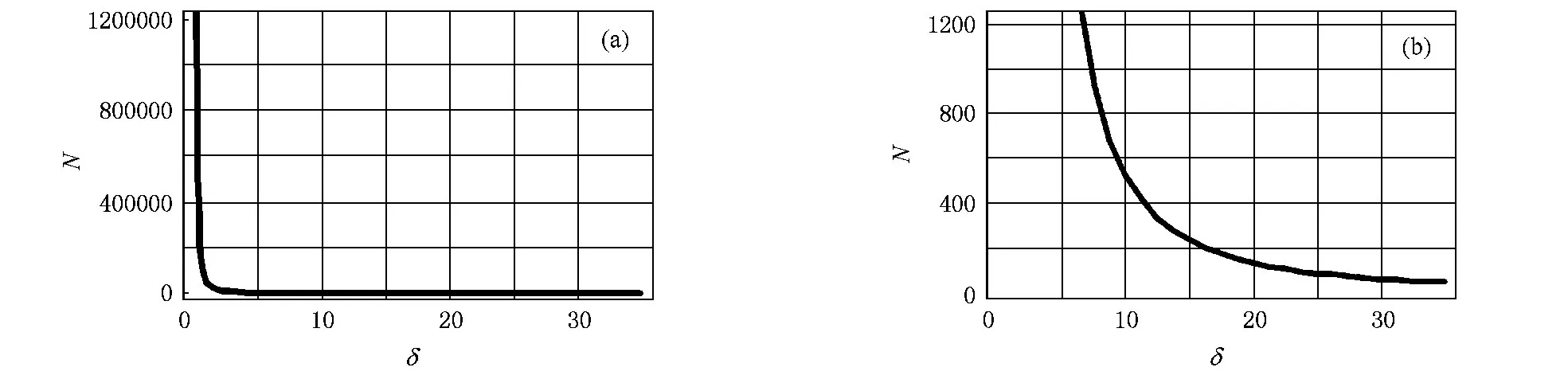
图2 精确扫描修正相位点光子计数输出总和与扫描精度之间的关系 (a)为扫描精度范围为0—35°之间的曲线;(b)为扫描精度在5°—35°之间的曲线

2.4.讨 论

以上我们一共选取了五个相位点完成了满足系统精度的相位漂移参数的扫描过程,这一扫描过程是在单光子水平上进行的,我们可以将该方法称为“五点法”相位漂移扫描方法.通过和文献[12]与文献[24]给出的扫描曲线进行对比分析,该方法能够较好地和实验数据相符合.对文献[24]中的全部数据进行了计算,得出的粗扫描漂移参数的波动范围小于文献[24]中粗扫描过程的精度个结果表明,该方法在单光子水平上进行相位漂移参数的扫描是可行的.和逐点扫描的方法相比,该方法可以在满足扫描精度的基础上,大大节省扫描时间,提高系统密钥分发的占空比.

3.结 论

我们提出了一种相位编码量子密钥分发系统中干涉相位漂移主动补偿的新方法,并将这种方法和相关文献中的补偿结果进行了详细的对比分析,结果表明,该方法可以在满足系统精度要求的条件下以更短的时间得到相位漂移参数并进行实时主动补偿,可使量子密钥分发系统在脱离实验室环境的情况下长期稳定工作,并进一步提高了密钥分发的系统占空比.该方法工作在单光子水平,不需要额外增加系统硬件,可用于目前常用的相位编码量子密钥分发系统,包括双不等臂M-Z干涉仪结构的系统以及差分相位编码系统等.

[1]Bennett C H,Brassard G1984Proceedings of the IEEE International ConferenceonComputers,Systems,andSignalProcessing, Bangalore,India,New Y ork:IEEE 175

[2]Bennett C H 1992Phys.Rev.Lett.68 3121

[3]Bennett C H,Bessette F,Brassard G,Salvail L,Smolin J 1992J. Crypto.5 3

[4]Hughes R,Morgan G,Peterson C 2000J.Mod.Opt.47 533

[5]Stucki D,G isin N,Guinnard O,Ribordy G,Zbinden H 2002New J.Phys.4 41

[6]Huges R,Nordholt J,Derkacs D,Peterson C G 2002New J. Phys.4 43

[7]G obby C,Yuan ZL,Shields AJ 2004Appl.Phys.Lett.84 3762

[8]Mo X F,Zhu B,Han Z F,Gui Y,Guo G2005Opt.Lett.30 19

[9]WangJ D,Lu W,Zhao F,Liu XB,Guo B H,ZhangJ,Huang Y X,Lu YQ,Liu S H 2008Acta Phys.Sin.57 4214(in Chinese) [王金东、路 巍、赵 峰、刘小宝、郭邦红、张 静、黄宇娴、路轶群、刘颂豪2008物理学报57 4214]

[10]Hu H P,ZhangJ,WangJ D,Huang Y X,Lu YQ,Liu S H,Lu W2008Acta Phys.Sin.57 5605(in Chinese)[胡华鹏、张静、王金东、黄宇娴、路轶群、刘颂豪、路 巍2008物理学报57 5605]

[11]G isin N,Ribordy G,Tittel W,Zbinden H 2002Rev.Mod.Phys. 74 145

[12]Chen W,Han Z F,Mo X F,Xu F X,Wei G,Guo G C 2008 Chinese Science Bulletin.53 9

[13]Zbinden H,Gautier J D,G isn N,Huttner B,Muller A,Tittel W 1997Electron Lett.33 586

[14]Muller A,Herzog T,Huttner B,Tittel W,Zbinden H,G isin H 1997Appl.Phys.Lett.70 793

[15]Vakhitov A,Mkarov V,Hjelme D R 2001J.Mod.Opt.48 2023

[16]Ribordy G,Brendel J,Gautier J D,G isin N,Zbinden H 2001 Phys.Rev.A 63 012309

[17]Nambu Y,Hatanaka T,Nakamura K 2004Jpn.J.Appl.Phys. 43 L1109

[18]Hongjo T,Inoue K,Takahashi H 2004Opt Lett.29 2797

[19]Nambu Y,Y oshino K,T omita A 2006Jpn.J.Appl.Phys.45 5344

[20]T ownsend P D,RarityJ G,Tapster P R 1993Elect.Lett.29 634

[21]Yuan ZL,Shields A J 2005Opt.Exp.13 660

[22]Zavriyev A,Leverrier A,Denchev V,Leverrier A 2007J.Mod. Opt.54 305

[23]Makarov V,Brylevski A,Hjelme D R 2004Appl.Opt.43 4385

[24]Brylevski A,Hjelme D R,Makarov V 2002MasterThesis (Norwegian University of Science and Technology)

PACC:4250,0367,4230Q,9575K

An effective active phase compensation method for quantum key distribution system＊

Wang Jin-Dong1)†Qin Xiao-Juan2)Wei Zheng-Jun1)Liu Xiao-Bao1)Liao Chang-Jun1)Liu Song-Hao1)
1)(Laboratory of Photonic Information Technology School for Information and Optoelectronic Science and Engineering,South China Normal University Guangzhou 510006,China)
2)(Guangdong Radio&TV University,Guangzhou 510091,China)

15 February 2009;revised manuscript

15 April 2009)

Quantum key distribution(QK D)system must be robust enough in practical communication.The system performance is notably affected by phase drift.For the fiber-based phase-encoded quantum key distribution system,the Faraday-Michelson QK D scheme can auto-compensate the birefringence of fiber,but phase drift caused by environment variations is still a serious problem in practical operation.In this paper,the major schemes to compensate for the phase drift are analyzed in detail and an“fivephase”effective active phase compensation method is proposed.The comparison with other two major active phase compensation schemes also given.The result shows that this method uses less time to acquire the parameter of phase drift with the same precision and it can be used in phase-encoded QK D systems without introducing additional devices.

quantum cryptography,phase-encoded,phase drift,active phase compensation

＊广州市科技支撑计划(批准号:2008Z1-D501)和广东省工业攻关项目(批准号:2007B010400009)资助的课题.

†通讯联系人.Email:jindongwqkd@126.com

＊Project supported by the Key Projects in the Guangzhou Science&Technology Pillar Program(Grant No.2008Z1-D501)and by the Guangdong Key Technologies R&D Program(Grant No.2007B010400009).

†Corresponding author.E-mail:jindongwqkd@126.com