基于纤维模型的钢筋混凝土结构动力弹塑性分析1

吕 杨徐龙河李忠献丁 阳

1）天津大学建筑工程学院，天津300072

2）北京交通大学土木建筑工程学院，北京100044

基于纤维模型的钢筋混凝土结构动力弹塑性分析1

吕 杨1）徐龙河2）李忠献1）丁 阳1）

1）天津大学建筑工程学院，天津300072

2）北京交通大学土木建筑工程学院，北京100044

采用纤维单元模型和实体单元模型对一个钢筋混凝土柱进行了动力弹塑性分析，结果表明，截面纤维模型能以很小的计算成本达到实体单元模型的计算精度，并且和试验结果拟合较好。同时，对一个3层钢筋混凝土框架结构进行的动力弹塑性分析表明，纤维单元模型能很好地解决各种非线性问题，适合于强震作用下结构整体动力弹塑性分析。

动力弹塑性分析 钢筋混凝土柱 LS-DYNA 纤维模型 钢筋混凝土框架

引言

影响建筑结构灾变过程的控制参数很多，完全基于试验的研究方法因受到试验设备和试验经费的限制，目前大多以数值模拟辅以少量模型试验进行研究，显然快速精确的数值模拟方法是解决上述问题的关键。目前，大型通用有限元软件建立结构分析模型的方法主要有实体单元模型和梁单元模型，实体单元模型因为建模复杂（Makoto等，2009）、计算成本过高，只能用于结构构件层次上的分析或小型建筑结构的整体分析，而梁单元模型又由于计算精度不高，一般只能用于结构整体模态分析或定性分析。有鉴于此，很多学者在通用有限元软件的基础上进行了二次开发，建立了用户自定义单元模型平台（林旭川等，2007；陆新征等，2007；方明霁等，2008；秦从律等，2005），但是由于平台开发难度大，还可能出现求解过程不够稳定，不能很好处理材料负刚度等问题，目前还不能满足大多数人的需求。

为了对比实体单元模型与纤维单元模型的计算精度和计算成本，本文用 LS-DYNA有限元程序分别对一个钢筋混凝土柱建立了纤维单元模型和实体单元模型进行动力弹塑性分析。分析结果表明，LS-DYNA软件中的截面纤维模型能以很低的计算成本达到较高的求解精度。同时，对一个3层钢筋混凝土框架结构进行强震作用下弹塑性时程分析，结果表明纤维单元模型能很好处理各种非线性问题，求解过程稳定，适合于强震作用下整体结构的灾变过程分析。

1 内力计算

通过将截面离散成纤维，再分别给不同的纤维赋予相应材料的滞回性能，对各纤维应力数值积分计算截面内力（Schwer，2003），轴力为：

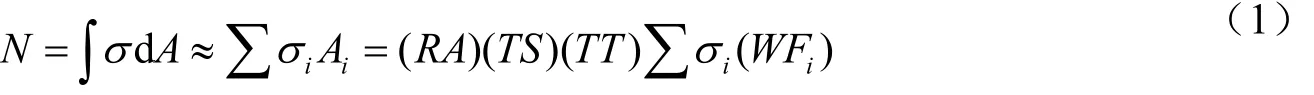
式中，RA为定义截面形式参数；TS和TT为截面尺寸；σi为第i个积分点轴向应力；WTi为第i个积分点相对截面面积。弯矩为：

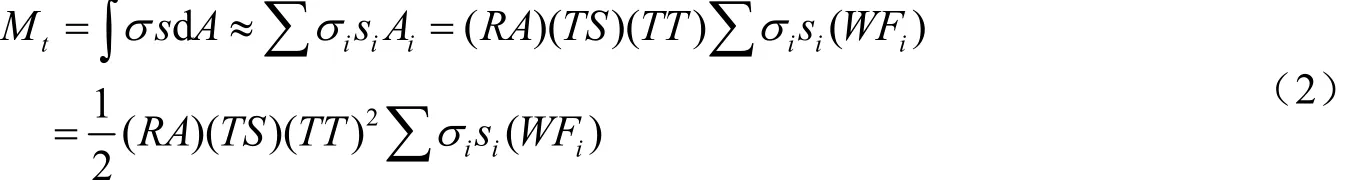
式中，si为相对坐标。同理：

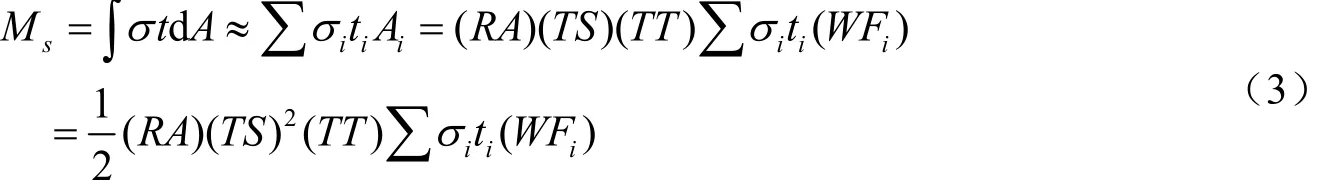
式中，ti为相对坐标。

2 钢筋混凝土柱动力弹塑性分析

2.1 模型几何参数

为验证截面纤维单元计算精度和成本，分别建立实体单元模型和纤维单元模型，并对Hideaki等（2004）文章中的正方形截面钢筋混凝土柱进行动力弹塑性时程分析。方形截面钢筋混凝土悬臂柱柱高2.5m，纵向配置48根直径10mm的钢筋，配筋率约为0.95%，箍筋为间距75mm、直径6mm的钢筋，材料参数同Hideaki等（2004）。柱顶配重约36t，柱底应力为1.0MPa，质心点高度为3.0m。地震动输入为双向Kobe地震波，加速度峰值N-S向为642gal，E-W向为666gal，时间步按1/2缩放。

2.2 有限元模型

纤维单元模型中将柱截面离散成100个混凝土网格和48个钢筋网格。沿轴向离散成25个纤维段和2个用于模拟柱顶附加质量的刚性梁单元。混凝土采用Kent等（LS-DYNA，2006）建议的材料本构模型。钢筋采用考虑塑性流动的弹塑性强化模型。

实体单元模型中钢筋与混凝土分别建模。混凝土采用正六面体单元模拟，单元边长为30mm；钢筋采用空间梁单元，梁单元长度 30mm；钢筋混凝土之间的粘结滑移采用一维滑动接触模型模拟（Schwer等，2005），粘结滑移相关参数（Weatherby，2003）如表 1所示。

在实体单元模型中，混凝土采用改进的 K&C混凝土模型（Schwer等，2005），该模型在保留 K&C模型优点的同时，在模型参数的确定方面作了简化。在使用时用户仅仅需要提供混凝土的轴心抗压强度（Schwer等，2005）。钢筋采用弹塑性强化模型模拟。

表1 粘结滑移参数取值Table 1 Parameters of one-dimensional slide line

3 结果分析

采用两种数值模拟方法所得柱顶加速度时程曲线和位移时程曲线如图1—图4所示。

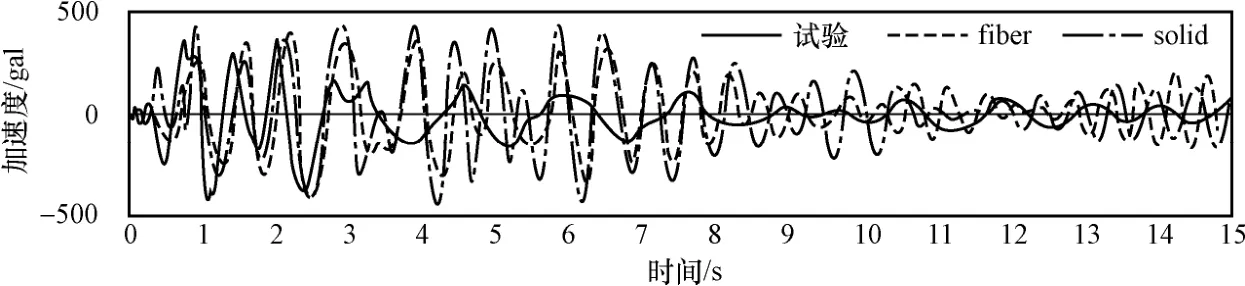
图1 X方向位移时程曲线Fig.1 Displacement time history in X direction

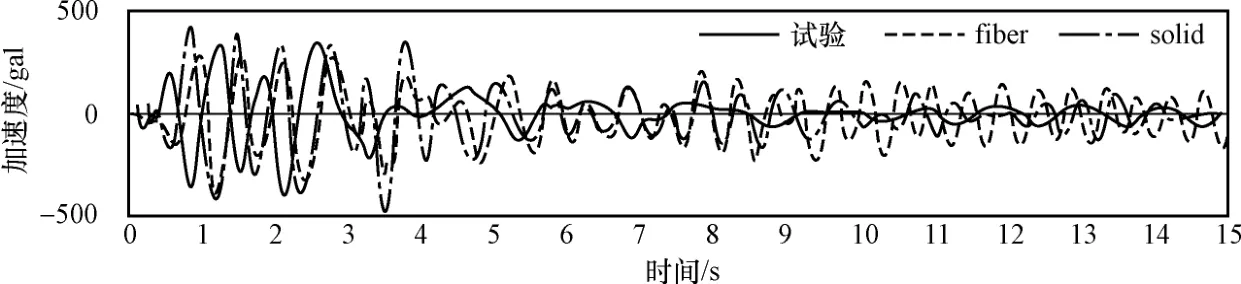
图2 Y方向位移时程曲线Fig.2 Displacement time history in Y direction

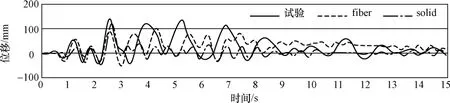
图3 X方向加速度时程曲线Fig.3 Acceleration time history in X direction

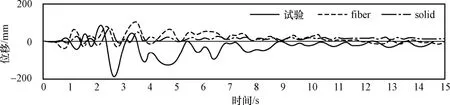
图4 Y方向加速度时程曲线Fig.4 Acceleration time history in Y direction

由上述位移时程曲线可以看出，X方向位移时程符合较好；在Y方向位移时程中，试验结果较数值模拟偏大；而在加速度时程中，实体单元模型结果较纤维模型和试验结果偏大。总体来说，纤维单元模型与实体单元模型结果相近，与试验结果有一些差别，但大体上基本符合，所以用实体单元模型或者纤维单元模型进行数值分析都是可行的，但纤维单元模型计算成本远低于实体单元模型。

3 钢筋混凝土框架结构弹塑性分析

3.1 框架结构模型

分析对象为 3层钢筋混凝土框架结构，结构层高、柱网尺寸、纵梁截面尺寸、横梁截面尺寸与梁益等（2007）相同。框架柱截面尺寸为600mm×600mm，沿四周对称配置8根直径为20mm的HRB335钢筋，配筋率约为0.77%；楼板厚度150mm，楼板下部纵筋配筋率为0.3%，盖筋配筋率0.2%；梁采用HRB335钢筋，配筋率为0.8%。框架梁柱混凝土采用C30，楼板混凝土采用C25；钢筋屈服强度取标准值335MPa，抗拉强度取435MPa。将填充墙按质量等效到楼板和柱子处，混凝土密度设置为 4500kg/m3，对应楼面恒荷为10.20kN/m2，活荷取2kN/m2，基本符合多高层建筑结构中均布荷载8—12kN/m2的标准。假定结构柱脚理想固结于地面，基地施加El Centro双向水平地震动，地震动加速度峰值都调幅为310gal。

3.2 有限元模型

由有限元分析软件LS-DYNA建立结构整体分析模型。模型中底层柱子采用纤维模型模拟，其余柱子及梁采用梁单元模拟，楼板采用LS-DYNA中的分层壳单元模拟。

3.3 结果分析

上述3层钢筋混凝土框架结构在双向地震动作用下，结构最终破坏状态如图5所示，相应X与Y方向底层柱顶位移时程曲线如图6所示。

图5 结构破坏状态Fig.5 The final failure model of the frame

图6 底层柱顶位移时程曲线Fig.6 Displacement time history at the first story

由于采用显示求解方法，截面纤维模型能很好地模拟结构在强震作用下的弹塑性响应。从图8所示位移时程可见，结构在5s时刻位移开始发散，可以认为结构已经破坏。图7所示为结构在6.9s时刻的破坏状态，可见框架结构底层是薄弱层，在强地震作用下，柱子沿两个方向产生塑性铰而发生整体倒塌。

4 结论

本文分别采用实体单元模型和纤维单元模型对一个钢筋混凝土悬臂柱进行了弹塑性时程分析。由于纤维单元可以按构件截面实际情况布置钢筋的位置，进而能以很低的计算成本较精确的模拟钢筋混凝土梁柱构件在地震动作用下的弹塑性反应。采用分离式建模的实体单元模型，能模拟钢筋与混凝土之间的粘结滑移等多种因素。但实际应用中，由于钢筋与混凝土分离式建模复杂，单元数量庞大，建立结构整体模型时还可能出现计算溢出的问题，因此，可以用实体单元模型建立构件或者小型建筑结构模型。

采用截面纤维模型对一个3层RC框架结构进行强震作用下的弹塑性时程分析，分析结果表明，本文所述的纤维单元模型因采用LS-DYNA集成的求解器，所以能很好地解决因材料、几何大变形等产生的强非线性问题，并且计算成本低，适合用于结构整体分析。

综上所述，实体单元模型可用于单个构件精细化分析或小型结构整体分析，并且还能模拟混凝土剥落过程，而对常见工程结构整体模型，截面纤维单元模型能以较低的计算成本满足工程计算精度。

方明霁，李国强，孙飞飞等，2008. 基于多弹簧模型的空间梁柱单元（I）：理论模型. 计算力学学报，25（1）：129—133.

梁益，陆新征，李易等，2007. 3层RC框架的抗连续倒塌设计. 解放军理工大学学报（自然科学版），8（6）：659—664.

林旭川，陆新征，缪志伟等，2007. 基于分层壳单元的RC核心筒三维全过程有限元分析. 见：第11届高层建筑抗震技术交流会论文集. 昆明：184—189.

陆新征，张炎圣，江见鲸，2007. 基于纤维模型的钢筋混凝土框架结构爆破倒塌破坏模拟. 爆破，24（2）：1—6.

秦从律，张爱晖，2005. 基于截面纤维模型的弹塑性时程分析方法. 浙江大学学报（工学版）， 39（7）：1003—1008.

Hideaki N., Shigeki U., 2004. Dynamic Response Characteristic of Reinforced Concrete Column Subjected to Bilateral Earthquake Ground Motions. See: 13th World Conference on Earthquake Engineering Vancouver, B.C., Canada, 2004: Paper No. 576.

LS-DYNA, 2006. Keyword User's Manual. Livermore, California: Livermore Software Technology Corporation.

Makoto O., Tomoshi M., Masayuki K. et al., 2009. High-precision finite element analysis of elasto-plastic dynamic responses of super-high-rise steel frames. Earthquake Engineering and Structural Dynamics, 38: 635—654.

Schwer L., 2003. LS-DYNA Beam Elements: Default and User Defined Cross Section Integration. See: 4th European LS-DYNA Users Conference, Ulm, Germany, 2003: HI31—HI48.

Schwer L.E., Malvar L.J., 2005. Simplified Concrete Modeling with *MAT_CONCRETE_DAMAGE_REL3. JRILS-DTNA USER WEEK, 2005: 1—14.

Weatherby J.H., 2003. Investigation of Bond Slip between Concrete and Steel Reinforcement under Dynamic Loading Conditions. Mississippi, Louisiana State University.

Dynamic Elasto-Plastic Analysis of Reinforced Concrete Structure Based on Fiber Model

Lu Yang1), Xu Longhe2), Li Zhongxian1)and Ding Yang1)

1) School of Civil Engineering, Tianjin University, Tianjin 300072, China
2) School of Civil Engineering, Beijing Jiaotong University, Beijing 100044, China

The fiber model and solid element model are established to analyze the dynamic elasto-plastic response of a RC column respectively in this paper. Our results show that the fiber model can simulate the shake table test as accurate as solid element model, and numerical simulation coincides with the experimental results well with a small calculation of cost. Moreover, a reinforced concrete frame is analyzed, and simulation results indicate that the fiber model can solve strong nonlinear problem lightly, which can be used to analyze the structures under strong seismic excitations.

Dynamic elasto-plastic analysis; Reinforced concrete column; LS-DYNA; Fiber model; Reinforced concrete frame

吕杨，徐龙河，李忠献，丁阳，2010. 基于纤维模型的钢筋混凝土结构动力弹塑性分析. 震灾防御技术，5（2）：257—262.

国家自然科学基金重大研究计划重点支持项目（90815025；90715032）；国家自然科学基金青年科学基金项目（50808013）；天津市应用基础与前沿技术研究计划重点项目（09JCZDJC25200）

2010-03-09

吕杨，男，生于1984年。博士研究生。主要从事结构抗震研究。E-mail: lvyangtju@163.com