基于身份密钥交换的安全模型

刘文菊，张俊伟，马建峰，杨超，李兴华

（1. 天津工业大学 计算机科学与软件学院，天津 300160；2. 西安电子科技大学 计算机网络与信息安全教育部重点实验室，陕西 西安 710071）

1 引言

1984年，Shamir首次提出了基于身份（ID-based）的非对称密码系统的概念[1]。与传统的非对称密码系统不同，ID-based密码系统简化了密钥管理的过程：用户的公钥可以由用户的身份信息产生，而私钥由一个可信的密钥生成中心产生。随着ID-based密码学的发展，一些基于身份的密钥交换(ID-based KE)协议被提出[2,3]。在 AKE 安全模型[4]下，Chen和 Kudla研究了可证安全的 ID-based KE[4]。在Canetti-Krawczyk模型(CK 模型)下，ID-based KE的可证安全模型也被提出[5,6]。但AKE安全模型和CK模型[7]仅仅保证ID-based KE协议在独立运行情况下的安全性，而不能保证协议组合情况下的安全性。

通用可组合安全框架(UC, universally composable framework)[8]可以保证协议的组合安全性，即在UC框架下证明安全的协议，在该协议与其他协议并发运行的情况下，或者该协议作为一个系统的组件时，仍能保证协议的安全性。理想函数是UC安全框架中十分重要的部分，它扮演着一个不可攻陷的可信角色，能够完成协议所执行的特定功能。目前已经定义了多个理想函数，如认证消息传输、安全消息传输、密钥交换、公钥加密、签名、承诺、不经意传输[9]等。

在UC框架下设计协议的困难和核心内容就在于形式化和抽象一个完美的并且可以安全实现的理想函数。Nishimaki等在 UC框架中提出了ID-based Encryption和ID-based Signature的理想函数[10,11]。但在UC框架中针对ID-based KE还没有形式化的定义。

本文在UC框架下提出了基于身份密钥交换的安全模型。针对ID-based KE的安全需求，在攻击模型添加了攻陷密钥生成中心的能力，并设计了ID-based KE的理想函数。在新的攻击模型和理想函数下，提出的模型既保证了ID-based KE的通用可组合安全性，又保证了一个重要安全属性——密钥生成中心前向保密性(KGC-FS, key generation center forward secrecy)。针对理想函数的实现问题，证明了带有密钥确认属性(key confirmation)的 Chen-Kudla协议能安全实现ID-based KE的理想函数。

本文剩余部分组织如下：第2节介绍了UC框架；第3节在UC框架下给出了满足ID-based KE安全需求的理想函数；第4节证明了带有密钥确认属性的Chen-Kudla协议能安全实现ID-based KE的理想函数；第5节是结束语。

2 UC框架

UC框架如图1所示。首先，UC框架定义了现实环境。现实环境描述协议的真实运行情况，其中所有参与方在真实敌手攻击A存在的环境下运行真实协议。其次，UC框架定义了理想环境用来描述密码协议的理想运行。在理想环境下，存在虚拟参与方，理想敌手S和一个理想函数F。参与方之间以及敌手S与参与方不直接通信；所有参与方和敌手S均与理想函数交互。理想函数本质上是一个不可攻陷的可信角色，用来完成协议所需的理想运行和功能。在UC的安全框架中，环境Z来模拟协议运行的整个外部环境（包括其他并行的协议、攻击者等），Z可以与所有的参与者以及攻击者 A和 S直接通信，Z不允许直接访问理想函数F。

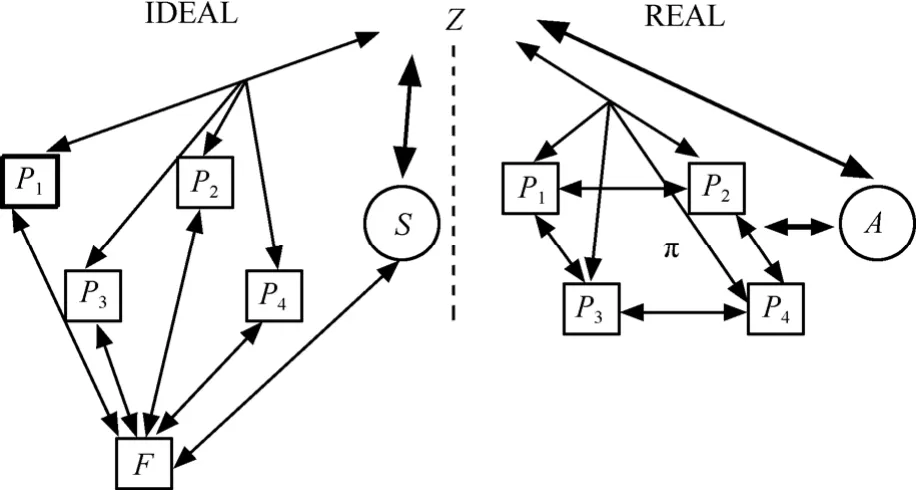
图1 UC 框架

1) UC仿真

协议π仿真理想函数F当且仅当对于任意现实敌手 A，存在理想敌手 S，使得任意环境 Z，至多以可忽略的概率来区分：存在真实敌手A及协议π的现实环境和存在理想敌手S及理想函数F的理想环境。如果协议π能UC仿真理想函数F，就称协议π在UC框架下安全实现了理想函数F，也称π是UC安全的。

2) UC仿真的传递性

如果协议π1能UC仿真协议 π2并且协议π2能UC仿真协议π3，那么π1可以UC仿真π3。

3) 组合定理[8]

如果协议ρ实现理想函数F，且π 是F-混合模型[8]下的协议，那么协议 πρ/F（用协议 ρ 替换协 π中的理想函数F所得到的组合协议）UC仿真F-混合模型下的协议π。特别地，如果协议π在F-混合模型下实现理想函数 G，那么协议 πρ/F也实现了理想函数G。

3 ID-based KE的理想函数

3.1 攻陷KGC

在UC框架中，给攻击者增加了攻陷KGC的能力(记为CorruptKGC)。当攻击者发起CorruptKGC攻击后，攻击者可以获得 KGC的内部状态，即系统主密钥，这就意味着所有参与方的长期私钥泄漏。同时，KGC被标记为 corrupted；所有参与者被记为compromised（compromised表明该参与方的长期密钥已经泄漏）。需要特别指出的是：由于KGC的特殊性，这里假定 KGC不能被已有的 Corrupt攻陷，只能被CorruptKGC攻陷。

3.2 理想函数 F iKdKGEC

理想函数KGCidKEF 如下。

Setup

当从KGC收到 (Setup, sid, KGC)：

· 将(Setup, sid, KGC)发送给 S；

· 当从S收到(Set, sid, PKs), 给KGC输出(Set,sid, PKs)；

· 记录(KGC, PKs)并标记为 fresh。

Extract

当从 Pi收到(Extract, sid, IDi, PKs’)：

· 如果记录(KGC, PKs’)存在, IDi是 Pi的身份标识, 那么在ID-Reg中记录(IDi, Pi), 标示为fresh.否则, 不记录；

· 将(Extract, sid, IDi, PKs’)发送给 S, 随后从 S收到(Received, sid)；

· 将(Extracted, sid, IDi, PKs’)发送给 Pi和KGC(如果 PKs’没有被记录,或者 IDi不是 Pi的身份标识, 不发送这个消息)。

Key Exchange

当从Pi收到 (NewSession, sid, Pi, Pj, role, IDi,PKs’)：

· 将(NewSession, sid, Pi, Pj, role, IDi, PKs’)发送给S；

· 如果这是第一个 NewSession 质询并且存在记录(KGC, PKs’)和(IDi, Pi), 或者这是第二个NewSession 质询且(Pj, Pi, IDj)已被记录, 存在记录(KGC, PKs’)和(IDi, Pi), 那么记录(Pi, Pj, IDi)。

当从 S收到 (NewKey, sid, Pi, IDi, sk), 其中|sk|=k, 如果存在记录(Pi, Pj, IDi)且这是对Pi的第一次NewKey质询, 那么∶

· 如果 Pi或 Pj被攻陷,输出(sid, sk)给 Pi；

· 否则, 如果存在记录(Pj, Pi, IDj), 且已经给Pj发送过密钥 sk’,输出(sid, sk’)给 Pi；

· 否则, 选取一个新的随机数sk’（长度为k）作为密钥, 发送(sid, sk’)给 Pi。

当从S收到 (Corrupt, sid, Pi)：

如果Pi不是KGC且Pi还没被攻陷, 那么：

· 将 Pi标记为 corrupted；

· 如果记录(IDi, Pi)未泄露, 标示 Pi为compromised。

当收到来自敌手 S的消息(CorruptKGC, sid,KGC)∶

如果KGC未被攻陷, 那么：

· 将KGC标示为corrupted；

· 如果存在记录(KGC, PKs’), 那么 ID-Reg 中的所有未泄露记录标示为compromised。

其中Setup：当KGC发送系统建立的请求时，理想函数将这个请求发送给敌手S。S决定系统的公共参数并且将这些参数发送给KGC。

Extract：当参与方发出注册请求时，理想函数在ID-Reg中记录这个ID并将这个请求发送给敌手S。当收到S的响应时，将结果发送给参与方和KGC。

Key Exchange：在会话密钥产生前，如果任意一方被攻陷，敌人S可以决定会话密钥的值。否则，FiKdKGEC生成一个随机数作为会话密钥。

3.3 KGC-FS

KGC-FS：即使KGC被攻陷（这意味着系统主密钥泄露，进而导致系统中所有参与方的长期私钥泄露），任何已经建立的密钥仍是安全的。KGC-FS属性也保证了另一个重要属性——无密钥托管（without key escrow）。

KGC-FS对于ID-based KE是一个非常重要的属性。一方面，如果 ID-based KE协议不能保证KGC-FS，那么KGC就可以获得系统中任意两方协商的会话密钥，进而得到双方交换的消息内容。如果通信双方希望保证他们通信的机密性，甚至也不希望KGC获得他们之间的通信内容，那么ID-based KE协议就必须满足KGC-FS，即无密钥托管。另一方面，如果不能保证KGC-FS，那么，当KGC被攻陷时，敌人可以获得所有系统中已经建立的会话密钥，进而得到系统中所有的已经通信的消息内容。

理想函数 FiKdKGEC满足KGC-FS。原因如下：FiKdKGEC会对CorruptKGC做出相应的响应。但是，在仅仅发生CorruptKGC的情况下，产生的会话密钥仍然是随机的，即敌手不能决定会话密钥的值，不能威胁会话密钥的安全。

4 实现ID-based KE的理想函数

本节证明带有密钥确认属性的 Chen-Kudla协议（记为πidKE）能安全实现理想函数 FiKdKGEC。

需要说明的是，在Setup和Extract阶段，协议运行在一个安全的信道下。这样可以确保系统主密钥和参与方长期私钥在密钥交换前的安全性。下面给出了协议πidKE的详细描述。

Setup

当KGC输入(Setup, sid, Ps)：

· H是散列函数，f和g是伪随机函数；

Extract

当 Pi输入(Extract, sid, IDi, PKs’)，如果 PKs’存在且IDi是Pi身份标识：

· 令Qi=H(IDi), Pi的私钥为秘密地发送 Si给 Pi；

· 输出 (Extracted, sid, IDi, PKs’)。

参与方Pj的注册过程与Pi的过程类似。

Key Exchange

发起者Pi输入(Pi, Pj, sid, ID, initiator)，类似地,响应者输入(Pj, Pi, sid, ID’, responder)。

· Pi随机选择 a∈Zq*, 发送(Pi, sid, μ, α)给 Pj，其中,

· 收到(Pi, sid, μ, α)后, Pj随机选择令Pj计算并删除b，计算则其中 l为消息计数器，发送(Pj, sid,ν, β, l, σj)给 Pi；

· 收到(Pj, sid, ν, β, l, σj)后, Pi计算0)和并删除 a, 其中，然后, Pi用 κa’验证 σj的正确性，如果正确, Pi计算l’为消息计数器，发送(Pi, sid, l’, σi)给 Pj, 输出(sid, Pi, Pj, κd’)；

· 收到(Pi, sid, l’, σi)后, Pj用 κa验证 σi的正确性，如果正确, 输出(sid, Pj, Pi, κd)。

定理1如果BDH假设和CDH假设成立，f和 g是伪随机函数，则 πidKE安全实现理想函数FiKdKGEC。

证明令现实敌手为 A。构造理想敌手 S，对于任何环境Z仅能以一个可忽略的概率区分是：A与πidKE交互的真实环境(标记为REAL)和S与 FiKdKGEC交互的理想环境(标记为IDEAL)。

1) 构造S

首先构造内部状态仿真器I (如果g是伪随机函数，πidKE具有应答属性)。输入(κd, s, Pi, Pj)，I输出其中 r 是随机数且|r|=|κa|。有关应答属性和内部状态仿真器的详细内容请参阅文献[12]。

敌手S运行如下。

Setup

当S从 FiKdKGEC收到(Setup, sid, KGC)且KGC未被攻陷，S为A仿真πidKE并以(Setup, sid, KGC)为输入。

πidKE输出(Set, sid, PKs)后，当从 FiKdKGEC收到(Setup, sid, KGC)时，S将(Set, sid, PKs)发给 FiKdKGEC。

Extract

当S从 FiKdKG

EC收到(Extract, sid, IDi, PKs’)且 Pi未被攻陷，S将(Extract, sid, IDi, PKs’)作为输入运行πidKE。

πidKE输出(Extracted, sid, IDi, PKs’)后，当 S 从FiKdKGEC收到(Extract, sid, IDi, PKs’)时，发送(Received,sid)给 FiKdKGEC。

Key Exchange

当S从 FiKdKG

EC收到(NewSession, sid, Pi, Pj, role,IDi, PKs’)，即 Pi请求与 Pj运行密钥交换协议(会话标识为sid)，S以(sid, Pi, Pj, role)为输入运行πidKE。

当 A 发送 (Pi, sid, μ, α)给 Pj，S 仿真从 Pi到 Pj的消息(Pi, sid, μ, α)。同样，当 A 发送 (Pj, sid, ν, β, l,σj)给 Pi，σj为 MAC 值，S 仿真从 Pj到 Pi的消息(Pj,sid, ν, β, l, σj)。当 A 发送 (Pi, sid, l’, σi)给 Pj，σj为MAC 值，S 仿真从 Pi到 Pj的消息(Pi, sid, l’, σi)。

当 πidKE输出(sid, Pi, Pj, κ)时，S 发送(NewKey,sid, Pi, κ)给 FiKdKGEC。

CorruptKGC

当 A攻陷 KGC时，S发送(CorruptKGC, sid,KGC)给 FiKdKGEC。

Corrupt

当A攻陷Pi时，S发送(Corrupt, sid, Pi)给 FiKdKG

EC。在这种情况下，如果 FiKdKGEC已经发送密钥给Pi，那么S获得密钥 κ。另外，如果在发生攻陷时，Pi和 Pj都没有输出密钥，那么，S将πidKE中Pi的内部状态发送给A。如果在发生攻陷的时刻，Pi或Pj已经输出密钥，S应用内部状态仿真器I得到仿真的内部状态τi和τj，并且将τi发送给A作为Pi的内部状态(如果Pj被攻陷，那么A将得到τj)。

2) IDEAL和REAL的不可区分性

根据仿真器S，证明不可区分性分为以下3种情况：CORRUPT事件表示Pi或Pj至少有一个被攻陷（事件1）；NONE事件表示CORRUPT和CKGC均未发生（事件2）；CKGC表示KGC被攻陷，Pi和 Pj未被攻陷（事件 3）。然后，证明在这 3种事件下，IDEAL和REAL是不可区分的。

事件1CORRUPT

当CORRUPT事件发生时，S完美仿真了敌手A，因此，IDEAL和REAL是不可区分的。

事件2NONE

首先定义协议 π0、π1和 π2。π0：π0随机选取 γ1(或γ1’)和 γ2(或 γ2’)，然后 π0随机产生 κd和 κa，以及 MAC值。π1：与 π0相比，修改了计算 γ1(或 γ1’)和 γ2(或 γ2’)的方法。π1计算和类似地，和π2：与 π1相比，修改了计算和的方法。π2使用伪随机函数 f计算 κd和 κd’。类似地，π2使用 f计算 κa和 κa’。

π0随机选取 γ1(或 γ1’)和 γ2(或 γ2’)的值，随机产生会话密钥和MAC值，那么π0的输出为随机数。因此，从环境Z的角度，IDEAL和π0是不可区分的，即 IDEAL≈π0。

引理1如果BDH假设和CDH假设成立，π1和 π0是不可区分的，即

假设存在环境 Z以不可忽略的概率区分 π1和π0。在Z的基础上，能构造2个算法D1和D2。D1能在概率多项式时间内（PPT）以不可忽略的概率解决BDH问题，这与BDH假设相矛盾。类似地，D2可以成功解决CDH问题，这与CDH假设矛盾。

由于篇幅限制，这里简要地给出 D1算法的核心内容来说明D1如何利用Z来解决BDH问题。

D1选择x作为系统主密钥，xP作为系统公钥。

D1令 Pi的公钥为Pj的公钥为

D1激活 Z，运行协议 π0和 A，其中 μ=aP，ν=bP。

当Z输出1时，D1计算

因此，如果Z能以不可忽略的概率区分π0和π1，D1也能以不可忽略的概率解决 BDH问题。这与BDH假设相矛盾。D2与D1类似，这里不做赘述。

引理2如果函数f是伪随机函数，π2和π1是不可区分的，即

如果Z能以不可忽略的概率区分 π2和 π1，则能构造一个区分器区分伪随机函数f生成的数和随机数。这与函数f是伪随机函数相矛盾。

引理3如果函数g是伪随机函数，REAL和π2是不可区分的，即

证明过程与引理2类似。

根据 UC-仿真的传递性，如果 BDH假设和CDH假设成立，f和 g是伪随机函数，那么。即事件NONE发生时，Z仅能以可忽略的概率区分REAL和IDEAL。

事件3CKGC

事件CKGC发生时，Z只能以可忽略的概率区分REAL 和IDEAL。这与发生NONE事件的证明类似。唯一的区别在于π1≈π0的证明。在这里，π1和 π0的不可区分性仅仅依靠 CDH假设，而不是BDH 假设，因为 Z 可以计算

根据以上3种情况的分析，定理2得证。 □

5 结束语

本文在UC框架下提出了基于身份密钥交换的可组合安全模型。在攻击模型中添加了CorruptKGC，设计了ID-based KE理想函数KGCidKEF 。提出的模型满足了ID-based KE的通用可组合安全性和KGC-FS。同时，证明了带有密钥确认性质的Chen-Kudla协议可以安全实现理想函数KGCidKEF 。

[1] SHAMIR A. Identity-based cryptosystems and signature schemes[A].Advances in Cryptology-CRYPTO’84[C]. Springer-Verlag, 1984.47-53.

[2] CHEN L, KUDLA C. Identity based authenticated key agreement protocols from pairings[A]. CSFW'03[C]. 2003.219-236.

[3] 汪小芬, 陈原, 肖国镇. 基于身份的认证密钥协商协议的安全分析与改进[J]. 通信学报, 2008, 29(12)∶16-21.WANG X F, CHEN Y, XIAO G Z. Analysis and improvement of an ID-based key agreement protocol[J]. Journal on Communications,2008, 29(12)∶ 16-21.

[4] BELLARE M, ROGAWAY P. Entity authentication and key distribution[A]. Advances in Cryptology-Crypto’93[C]. 1993. 232-249.

[5] LI X H, MA J F, MOON S J. Security extension for the canetti-krawczyk model in identity-based system[J]. Science in China(F series), 2005, 48(1)∶ 117-124.

[6] ZHU R W, TIAN X J, WONG D S. A suite of enhanced security models for key compromise impersonation resilience and ID-based key exchange[EB/OL]. http∶//eprint.iacr. org/2005/ 455, 2005.

[7] CANETTI R, KRAWCZYK H. Analysis of key-exchange protocols and their use for building secure channels[A]. Proc EUROCRYPT 2001[C]. Springer-Verlag, 2001. 453-474.

[8] CANETTI R. Universally composable security∶ a new paradigm for cryptographic protocols[EB/OL]. http∶//eccc.uni-trier.de/eccc-reports/2001/ TR01-016/, 2001.

[9] 李凤华,冯涛,马建峰. 基于 VSPH的UC不经意传输协议[J]. 通信学报, 2007, 28(7)∶28-34.LI F H, FENG T, MA J F. Universally composable oblivious transfer protocol based on VSPH[J]. Journal on Communications, 2007,28(7)∶28-34.

[10] NISHIMAKI R, MANABE Y, OKAMOTO T. Universally composable identity-based encryption[A]. The 2006 Symposium on Cryptography and Information Security Hiroshima[C]. Japan, 2006.17-20.

[11] NISHIMAKI R, MANABE Y, OKAMOTO T. Universally composable identity-based encryption[J]. IEICE Trans Fundamentals, 2008,(E91-A) (1)∶ 262-271.

[12] CANETTI R, KRAWCZYK H. Universally composable key exchange and secure channels[A]. Eurocrypt 02[C]. 2002. 337-351.