优化军校医疗服务的数学模型

王体标 苏丽宣

公安海警学院 浙江宁波 315801

随着社会经济的发展，人们对医疗保健服务提出更高的要求。军队医疗保险的改革、军队医院的改革和建设，都要立足于患者的需求，最大限度满足患者的需要。军队的合理医疗[1]是在现有医疗保障体制下，在充分考虑军队特殊性的基础上，在军队投入和医院承受能力的范围内，在医疗保险和医疗服务双方共同遵从医疗保障系统的总目标下，利用有限的卫生资源，最大限度地满足提供医疗服务、接受医疗服务、提供医疗费用下降的需求，重点是保障军人的医疗需求，提高军人的健康水平。作为军校医院，常常面临卫生医疗设施不完善、基本医疗设备老化、医疗资金不充裕、改善医疗条件周期长等问题，不能提升医疗服务的满意度。

本文通过对学校官兵身体健康状况调查表的数据分析[2]，结合当前军队卫生经济“以医疗服务质量为核心”的根本原则，对医院的医疗服务提出合理的建议；在军队医疗财政预算一定的基础上，对医疗设备的引进提出优化决策，使得军人的医疗需求得到保障，以期达到合理医疗的目的。

1 调查分析及建议

通过对学校官兵健康状况调查以及医院前期的接诊和医疗记录的统计分析，可以得到反馈结果：1）轻症患者主要是以药物治疗可以有效解决所占的比例，不同时期各种病症的诊疗情况，给医疗保障有充裕的准备，及时做出预判性的诊疗方案和措施；2）重症或者疑难病症的患者比例，医疗条件的不足。为了优化医疗服务，建议医院做出健康信息经常性统计，体检记录及时反馈，通过掌握数据信息，合理安排医疗保障的费用，做到药物与医疗设备的优化分配，提高患者对医院服务的满意度。

2 优化医疗成本的数学模型

以医疗服务质量为核心的合理医疗，在经费有限的情况下，要处理好基础质量与规模发展的关系以及医院的建设发展和宏观决策，医疗设备配置要合理，利用有限的卫生资源，最大限度地保障军队官兵的医疗需求，提高他们的健康水平。军队医疗保险的改革为医疗服务提供了稳定的补偿机制，在军队投入和医院承受能力的基础上，合理引进医疗设备，才能提供高效益的医疗服务，保证医疗保险的良性运行。在运筹学中，这是一个整数规划问题，可用数学语言来描述，即可以用数学模型表示。

线性规划[3]（Linear Programming，简记为L）问题研究的是在一组线性约束条件下一个线性函数最优问题，其具有这样的特征：1）问题中要求有一组变量（决策变量），这组变量的一组定值就代表一个问题中的具体方案；2）存在一定的限制条件（约束条件），这些限制条件可以用一组线性等式或不等式来表示；3）有一个目标要求（目标函数），可以表示为决策变量的线性函数，并且要求这个目标函数达到最优（最大或最小）。

将这3个条件归结在一起，就得到线性规划问题。线性规划问题的标准形式是具有如下形式的问题：

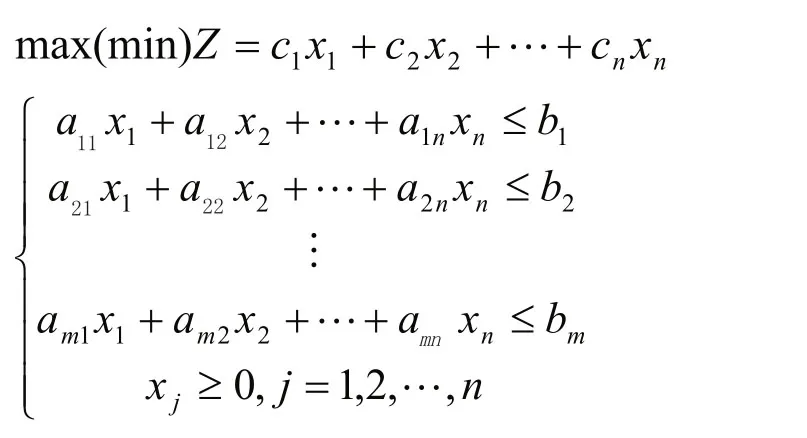
本文首先对健康信息进行数据分析，针对各种疾病的医疗记录，且听取专家的合理建议，由整数规划模型确定引进各种疾病的医疗设备[3]，来达到最佳的医疗效果。假设每年医疗设备的财政预算为C，对于医疗服务的评价通过患者的满意度来体现，提出优化模型：

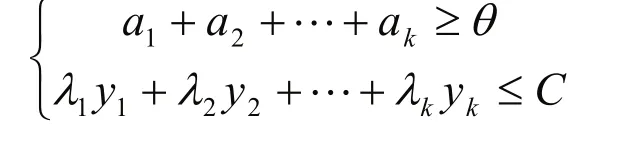
其中xi(i= 1 ,2, …k)是各类患者接受治疗满意指数，yi(i= 1 ,2,…k)是专家建议的各种疾患医疗设备成本，ai(i= 1 ,2,…k)是患者接受治疗比例系数，θ是既定医疗服务覆盖度。

医院的医疗服务是否适应军队医疗的需要，通过军队患者的满意度来评价，对于给定的医疗覆盖度，可以通过调整医疗设备的采购策略λi(i=1,2,…k)，使得在满足约束条件的基础上，目标函数达到最优。此数学模型的考察，不同于主成分分析方法，可以利用WinQSB软件进行处理。

对于高额费用的医疗设备，建议采取分期付款的方式，将优化决策应用到中长期的预算策略中，能够更好地解决医院采购决策的短期行为和滞后思维，使医疗设备的配置满足军队医疗服务的高要求[4]。

3 结束语

本文对医疗设备的引进，针对健康状况调查分析，提出有效的资金分配方案，改善军队的医疗条件，医疗服务的满意度得到保证。为了更好地利用医疗资源和更快地更新医疗设备，建议在满足部队医疗需要的基础上，也可以对外提供部分医疗有偿服务，实现军队医疗预算的补偿机制，促进医疗卫生条件的提高，切实保障广大官兵既能看得起一般的疾病，又能够及时有效地预防和治疗重大疾病。

[1]黄献风.医院推行政府采购管理的体会[J].广西市场与价格,2000(07):15-17

[2]杨孝光,侯凯文.军队医院门诊医疗费用统计核查系统设计与实现[J].医疗卫生装备,2009(05):48-49

[3]胡运权.运筹学基础及应用[M].北京:清华大学出版社,2004:10

[4]杨静宜,孙汉堂.关于军队医院强化医疗成本核算的思考[J].中国卫生经济,2005(08):23-25

[5]高永忠,杨月明,等.构建资源节约型医院的实践与效果[J].中国卫生经济,2009(10):36-38