变形三重介质低渗透油藏双渗流动模型

刘文超,张世明,刘晓燕,王 君

(1.中国石油大学,山东 东营 257061;2.中石化胜利油田分公司,山东 东营 257015; 3.中国石油大学,北京 102249;4.中石化胜利油田分公司,山东 东营 257200)

变形三重介质低渗透油藏双渗流动模型

刘文超1,张世明2,刘晓燕3,王 君4

(1.中国石油大学,山东 东营 257061;2.中石化胜利油田分公司,山东 东营 257015; 3.中国石油大学,北京 102249;4.中石化胜利油田分公司,山东 东营 257200)

低渗透油藏具有启动压力梯度,不仅考虑其渗流特征,还考虑应力敏感地层中介质的变形,建立变形三重介质低渗透油藏双渗流动模型。引入渗透率模数表达介质变形对渗透率的影响,结合低渗透情形下的非达西运动定律,推导出裂缝、溶洞与基岩同时发生形变、裂缝和溶洞同时向井筒供液的双渗流动数学模型,并求解,根据数值结果绘制试井样板曲线,同时对油藏参数进行了敏感性分析。

三重介质;变形;非达西渗流;低渗透油藏;井筒储集;表皮效应;试井

引 言

新疆塔河油田奥陶系属于典型的缝洞型碳酸盐油藏[1-3],具有明显发育的裂缝和溶洞。但是,该油田油井投产初期没有产能,经过压裂改造后才能获得较好的产量。这些地质特点和生产特征表明,该地层具有明显的三重介质特征和低渗透率的特点。国内外学者对于三重介质油藏的研究比较成熟,取得不少成果[4-13],但是对于低渗透三重介质油藏的研究却较少。该研究同时考虑启动压力梯度和压力敏感性的影响[14-15],建立变形三重介质低渗透油藏的双渗流动模型,并通过全隐式稳定差分格式求得该模型的数值解。利用该数值结果绘制无因次压力和压力导数的试井样板曲线,并对油藏参数进行了敏感性分析。

1 建立模型

1.1 物理模型

假定流体在基岩系统孔隙介质中不流动,只向裂缝和溶洞系统供给液源。流体通过裂缝和溶洞系统克服一定的启动压力梯度流入井筒,考虑基岩向裂缝、基岩向溶洞以及溶洞向裂缝的窜流,且均为拟稳态窜流。3种介质在地层压力降低时发生变形,可以通过含渗透率模数的状态方程来描述[11-12],其假设条件为[11-13]:

(1)三重介质油藏为低渗透油藏,裂缝和溶洞的初始渗透率不高,其中的液体流动均为单相层流动,符合低渗透情况下的非达西运动方程[15]:

式中:vr为基岩中流体的渗流速度,m/s;K为基岩渗透率,μm2;μ为流体黏度,mPa·s;p为地层压力,MPa;r为径向距离,m;λB为启动压力梯度, MPa/m。

(2)地层流体和地层岩石微可压缩。

(3)油藏均质且各向同性,横向无限延伸,顶、底界封闭。

(4)忽略重力和毛细管力的影响,假设地层压力梯度较小。

(5)每种介质 (裂缝、溶洞或基岩)的孔隙度与另一种介质的压力变动相对独立。

产妇分娩时综合评估指标与内容的确立，为临床会阴保护方式的规范奠定了一定的基础。具体分娩时产妇综合评估指标及内容还需通过不断的临床实践研究，进行进一步的修改与完善。

1.2 数学模型

按照上述物理模型进行数学公式推导,得到变形三重介质低渗透油藏单相微可压缩流体双渗流动的无因次数学模型[8,11-12]:

式中:pDi为各系统的无因次地层压力;pwD为无因次井筒压力;λ1、λ2、λ3分别为裂缝和基岩、裂缝与溶洞、溶洞与基岩之间的窜流系数;S1和S2依次为各系统的表皮系数;ωi为各系统的弹性储容比;γDi为各系统的介质变形系数;B1、B2分别为基岩系统和溶洞系统的无因次启动压力梯度;CD为无因次井筒储集系数;rD为无因次半径;tD为无因次时间。

1.3 数值模拟方法

模型中的偏微分方程均为强非线性,难以求出解析解,只能采用数值方法求解。对偏微分方程组进行全隐式差分离散,一阶导数采用一阶向前差商,二阶导数采用二阶中心差商。采用Newton迭代法[16]求解每时间层上的无因次压力,并且每一次迭代采用列主元三角分解法[16]求解线性方程组的解,程序运行速度较快,精度较高,算法较稳定。

2 无因次压力与压力导数的动态分析

2.1 标准无因次压力与压力导数曲线特征

2.2 无因次启动压力梯度的影响

由图 1可以看出,B1影响无因次压力和压力导数变化的整个过程,使得无因次压力和压力导数曲线的末端上翘。B1越大,无因次压力和压力导数也越大,曲线上翘的时间越早,上翘幅度也越大。具有不同B1值的压力导数曲线在后半段呈现“喇叭状”。这是由于启动压力梯度[12]的大小标志着流体在地层中产生流动的难易程度,因此在定产量情况下,启动压力梯度越大,压力变化越大、越快,曲线反映无因次压力上升越快,无因次压力导数越大。

图 1B1对无因次压力和压力导数的影响

2.3 变形系数的影响

由图 2可以看出,γD1对系统的整个流动过程均有影响。初期影响较小,随着无因次时间的增加,无因次压力和压力导数曲线逐渐发散;影响过渡段的高度,但不影响过渡段出现的时间;γD1越大,无因次压力和压力导数越大。由于渗透率模数越大,当地层压力下降时,渗透率下降速度越大,压力降落速度也就越快,反过来加速渗透率的减小,无因次压力和压力导数曲线均有一定的抬升,后期影响明显。

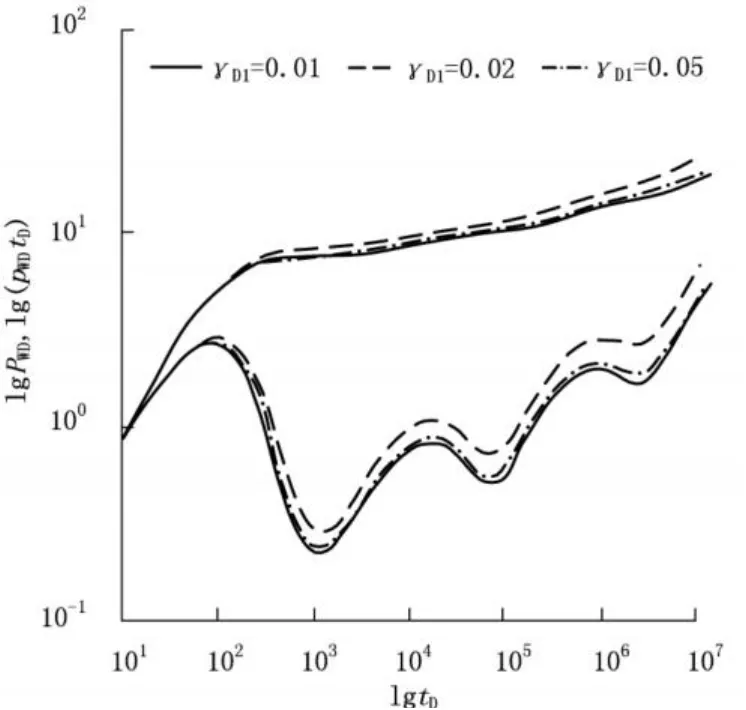
图 2 γD1对无因次压力和压力导数的影响

2.4 介质间窜流系数的影响

由图 3可以看出,λ1影响过渡阶段出现的早晚。λ1越大,过渡阶段出现的时间越早,对于后半段基本没什么影响,在无因次导数曲线上表现为:过渡阶段左移,第 1个“凹陷”深度没有变化,且随着无因次时间的推移,具有不同λ1值的无因次压力和压力导数曲线逐渐收敛。这与实际情况相符——窜流系数越大,对系统流动的影响越早。

图 3 λ1对无因次压力和压力导数的影响

2.5 弹性储容比的影响

由图 4可以看出,ω3越大,无因次压力导数曲线的第 1个“凹陷”越宽、越深;随着无因次时间的推移,无因次压力和压力导数曲线合为 1条曲线。因此,弹性储容比只决定介质间窜流时间的长短和窜流的强弱程度,与实际物理背景一致。

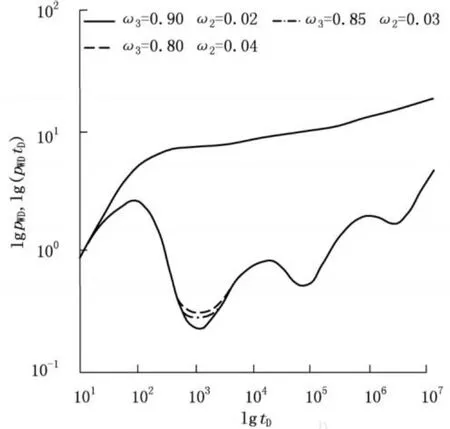
图 4 ω3对无因次压力和压力导数的影响

2.6 表皮系数的影响

由图 5可以看出,S1影响无因次压力曲线变化的整个过程。S1越大,无因次压力越大,整个无因次压力曲线向上抬升,无因次压力导数曲线的第1个“凸起”变尖,但对其以后的压力导数曲线部分没有影响。表皮系数的存在会造成附加压力降,使压力下降得更低,无因次压力更高。

图 5 S1对无因次压力和压力导数的影响

2.7 井筒储集系数的影响

由图 6可以看出,CD影响着早期阶段、第 1拟径向流阶段和第 1过渡阶段。CD越大,早期井筒储集阶段越长,进入第 1拟径向流的时间越晚,无因次压力导数曲线的第 1过渡阶段“凹陷”也越窄、越浅。井筒容积越大,卸载效应越严重,试井曲线上拟径向流段出现的时间越晚。虽然井筒储集阶段的时间非常短暂,但是卸载效应的作用时间较长。

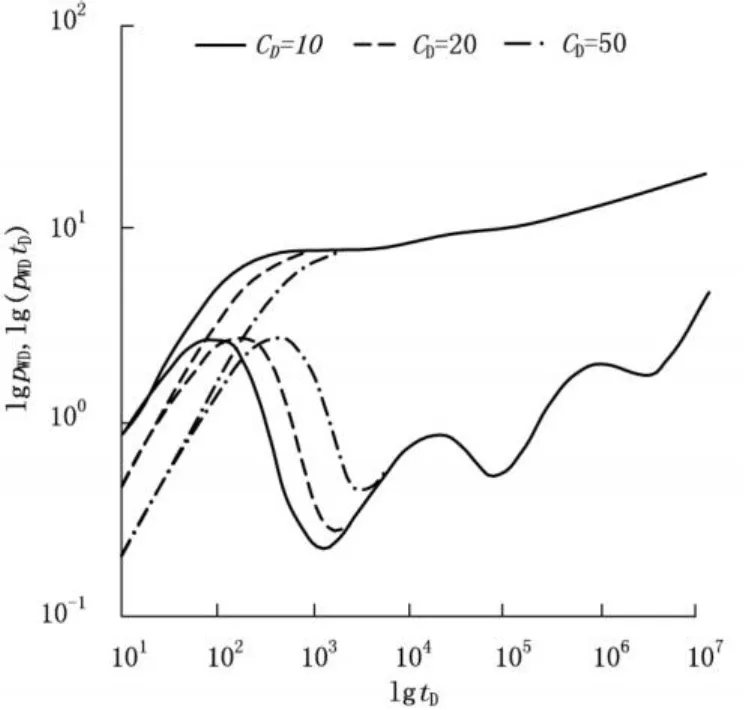
图 6 CD对无因次压力和压力导数的影响

3 结 论

(1)无因次启动压力梯度影响无因次压力和压力导数变化的整个过程,使得无因次压力和压力导数曲线的末端上翘;变形系数对系统的整个流动过程均有影响,无因次压力和压力导数曲线均有一定的抬升,后期影响更明显。

(2)介质间的窜流系数影响过渡阶段出现的早晚,窜流系数越大,对系统流动的影响越早;弹性储容比越大,无因次压力导数曲线的第 1个“凹陷”越宽、越深,弹性储容比只决定介质间窜流时间的长短和窜流的强弱程度。

(3)表皮系数影响无因次压力曲线变化的整个过程,表皮系数越大,无因次压力越大,整个无因次压力曲线向上抬升;井筒储集系数影响无因次压力和压力导数曲线的早期阶段、第 1拟径向流阶段和第 1过渡阶段。

[1]杨坚,姚军 .三重介质复合油藏压力动态特征研究[J].水动力学研究与进展:A辑,2005,20(4):419-425.

[2]孙鹏,袁玉玲,张永升,等 .数模技术在碳酸盐油藏早期开发油田的应用——以塔河油田 3区奥陶系油藏为例[J].新疆石油地质,2001,22(6):514-516.

[3]付学忠,赵斌,郭振莲 .塔河油田阿克亚苏区块低渗透层对水平井的影响[J].西部探矿工程,2008,7:108-110.

[4]Barenblatt G L,Zheltov Y P,Kocina.Basic concepts in the theory of seepage of homogeneous liquids in fissured rocks[J].Soviet J App Math and Mech,1960,(5):1283 -1303.

[5]Yeung K.An approximate analytical study of aquiferswith pressure-sensitive for mation permeability[J].Water Resource Research,1993,29(10):3495-3501.

[6]吴玉树,葛家理 .三重介质裂隙油藏中的渗流问题[J].力学学报,1984,14(1):81-84.

[7]姚军,王子胜,孙鹏,等 .超完善井条件下三重介质试井解释模型求解方法 [J].石油大学学报:自然科学版,2005,29(3):62-64.

[8]张利军,程时清,尹洪军 .双渗三重介质油藏试井分析[J].特种油气藏,2008,15(5):67-73.

[9]李秀军,李笑萍,李爱民 .考虑交接面阻力影响的三重介质复杂油藏的试井模型[J].特种油气藏,2009,16 (3):75-76.

[10]黄灿,李春兰,黄世军,等 .三重介质缝洞型油藏流动问题初探[J].特种油气藏,2009,16(4):64-66.

[11]张磊,同登科,马晓丹 .变形三重介质三渗模型的压力动态分析[J].工程力学,2008,25(10):103-109.

[12]王子胜,姚军 .缝洞向井筒供液时三重压敏介质油藏压力响应特征研究 [J].水动力学研究进展:A辑, 2006,21(1):85-89.

[13]同登科 .非线性渗流力学[M].北京:石油工业出版社,2003:134-140.

[14]阮敏,王连刚 .低渗透油田开发与压敏效应 [J].石油学报,2002,23(3):46-49.

[15]蔡明金,陈方毅 .考虑启动压力梯度低渗透油藏应力敏感模型研究 [J].特种油气藏,2008,15(2):69-72.

[16]李维国,黄炳家,同登科,等 .数值计算方法[M].东营:石油大学出版社,2004:32-39.

[17]李传亮 .油藏工程原理 [M].北京:石油工业出版社,2005:206-211.

编辑 姜 岭

TE312

A

1006-6535(2010)03-0073-04

20090925;改回日期:20100119

国家重大专项“裂缝性碳酸盐岩油藏开发关键技术”(2008ZX05014-004)

刘文超(1984-),男,2007年毕业于中国石油大学(华东)信息与计算科学专业,目前为该校在读硕士研究生,主要研究方向为应用数学与渗流力学。