基于马尔可夫转换模型的中国股市波动性研究
葛文雷,居新华
(东华大学 旭日工商管理学院,上海 200051)
基于马尔可夫转换模型的中国股市波动性研究
葛文雷,居新华
(东华大学 旭日工商管理学院,上海 200051)
证券价格的波动变化不仅影响衍生产品的价格也是政府管理金融市场、制定政策的依据。由于价格的波动往往呈现非线性的特征,文章利用马尔可夫转换模型对中国股票波动性进行估计。研究发现该模型可较好对我国上海证券市场股价波动性进行分类估计,并得到了证券市场波动的状态平滑概率图。在统计结果的基础上,还分析了我国市场波动性的成因和特点,并对政策的有效性进行评述。
马尔可夫转换模型;股票波动性;羊群效应
0 引言
证券市场作为金融体系的一个组成部分,在金融体系中具有重要的地位,证券市场波动对整个金融体系具有极其重要的影响。按照现代资本市场理论的观点,证券市场中各类因素的变化,都会不同程度地影响证券市场的供求关系并最终反映在证券市场价格变动上。因此价格波动就成为证券市场波动研究最核心的内容。
影响股票价格变动的因素可分为三类:(1)政策性因素,即管理层的政策干预行为,如股票交易规则变更、印花税的调整、通过新闻媒体发表的重要言论等。(2)外部性因素,主要指热钱,汇率等能影响股市流动性的因素。(3)周期性因素,每年初公司都会集中公布上年度年报,这段时间证券市场所接受的信息要比其他期间的要多,也会对股价的波动性产生影响。
国内学者对影响股价波动的因素进行过一些实证研究。但是这些研究往往针对证券市场某一特定时期进行统计,缺少对影响证券市场波动各种因素的整体分析:比如证券市场处于什么状态时,市场波动性会较小;这种关系是否具有时间一致性;市场波动性大的时候,是由单个因素影响还是几个因素共同影响。为解决上述问题,本文利用非线性下的马尔可夫转换模型对上证综指收益的波动率进行系统研究。把证券市场按股票收益率波动性的大小分成两类,通过状态转移矩阵研究不同时期的波动性大小,将不同时期波动性与该时期影响股市的因素联合分析,考察我国证券市场收益率变动的特点。
1 建立模型
马尔可夫转换模型是一种研究时间序列结构性变化的方法,它通过外部数据计算系统内部处于何种不可观测的体制的概率,来对系统进行分析和预测。马尔可夫转换模型由Hamilton(1989)首先建立,用于研究美国经济周期,Hamilton发现美国GNP增长率趋势函数可用一阶马尔可夫过程在两种不同的状态之间切换来表示,这两种状态反映了经济周期的状态:正向的经济增长状态和负向的经济衰退状态。所以马尔可夫转换模型适合研究不同状态下股市的波动率。
传统AR(p)模型下的股票波动率yt模型为:

其中 Xt=(yt-1,yt-2,…,yt-p),φ 为 Xt的回归系数,ut为白噪音。
在马尔可夫转换模型下,假设股票波动率y(t)存在k个服从AP(p)时变回归方程,它们分别代表k个不同状态,其中状态St为一不可见随机变量,且St是关于时间t齐次的,具有状态空间J=(1,2,…,k)一阶马尔可夫过程,其转移矩阵为:

其中

对任意 i∈J,都有

则基于马尔科夫转换下股票波动率可表示为:

其中 Xt=(yt-1,yt-2, …,yt-p),φSt为 Xt在状态 St下的回归系数,残差服从 ut(0,)分布,隐含状态 St满足式(3)和式(4)。
若隐含状态S=(Sp+1,…,Sn)是已知的,那么模型中不同状态下的未知参数Θ(包括AR(p)中截距、回归系数以及残差)可以通过对数极大似然估计方程得到:

这里γt-1代表在t-1时刻证券市场所有已知的信息,对Xj(j≤t)中所有的观察值均满足:

但是,状态S是通常是观察不到的,所以必须利用已知数据进行估计。当状态S是隐含的时候,AR(p)马尔可夫转换模型的需估计的未知参数Θ,除式(6)中的之外,还包括对转移概率矩阵P的估计。通常用下面办法解决该问题。
利用全概率公式,可将对数似然估计方差写成如下形式:
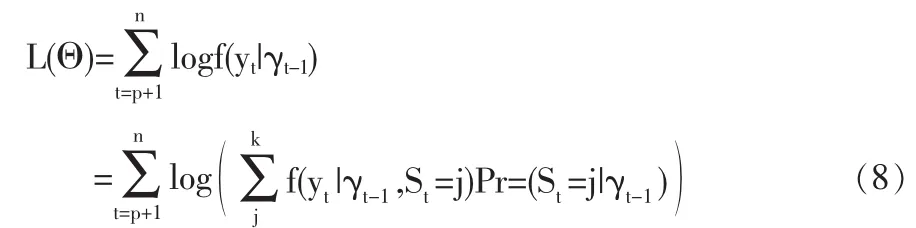
这里 f(yt|γt-1,St=j)符合式(6)。 并根据贝叶斯定理,Pr(St=j|γt-1)可以写成

因此,对每个状态的初始概率进行估计后,AR(p)马尔可夫转换模型的对数似然估计方程可以利用式(8)和式(9)得到,同时利用极大似然估计法就可以确定每个参数的估计值。
马尔科夫状态转换模型中的状态变量虽然不可直接观察到,但可以通过上述方法推论任意时刻t状态的概率,基于t时刻得到的概率为过滤概率,基于全部观测值得到的概率为平滑概率,由于马尔可夫转换模型中的状态概率为内生决定,由数据自行分割、识别各状态期间,因而避免了研究者主观设定和选择问题。
2 参数估计
样本数据取自1993年1月1日至2008年7月1日上证综指每周收益率的波动率。数据来源色诺芬数据库(CCER)。上证综指每周收益率的时间序列如图1。
每周收益率的波动率RVOL通过下面方法得到:先将该周每日收益率的平方,将5天的数据求和,最后将得到的和开方,该波动率可以反映该周股票波动率的大小,如图2所示。
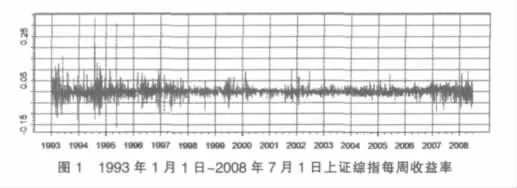
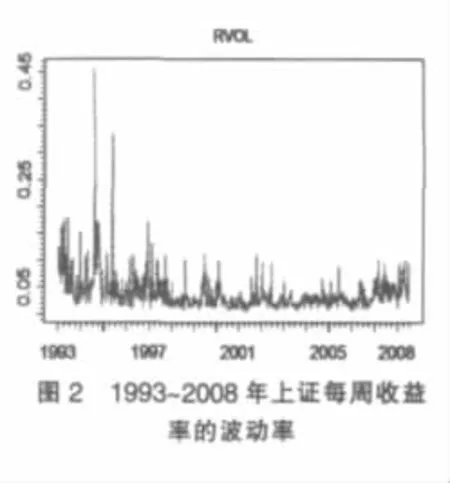

表1 样本数据的非线性检验
由于样本的时间跨度很长,所以首先对该时间序列进行非线性检验,结果如表1。
检验结果p-value小于0.05,所以统计意义显著,原假设不成立,即该序列存在非线性状态转移,因此不适合用单个时间序列对收益率的波动率进行估计。
本文利用AR(2)马尔可夫转换模型对数据进行研究。假设证券市场状态分为两种:稳定状态,和不稳定状态。稳定状态下,证券市场受信息冲击较小,其股指波动率也较小;不稳定状态下,证券市场受信息冲击较大,股指波动率也大。状态随机变量仅仅取1,2值,状态之间表现为非连续的转换。此时股指变动率的马尔可夫转换模型为:
当S=1时:

当S=2时:
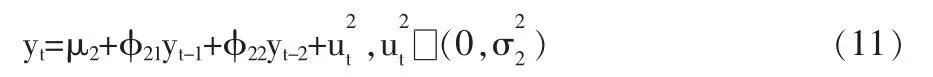
状态转移概率为:
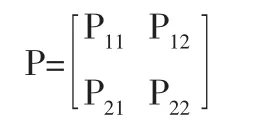
下面利用上一节提到的方法对参数 Θ=(μ1,μ2,φ11,φ12,φ22,σ1,σ2,P11,P12,P21,P22)进行估计。 在进行估计之前,为使数据更加正态化,将数据进行对数处理。利用处理后的数据,对马尔可夫转换模型进行参数估计的结果如表2所示。
从表2可知大多数参数的估计值都有重要的统计意义。由于这是基于对数的参数,所以还需将结果还原成要进行估计的参数Θ,还原后的马尔可夫转换模型为:
当S=1,股市状态稳定时:

当S=2,股市状态不稳定时:
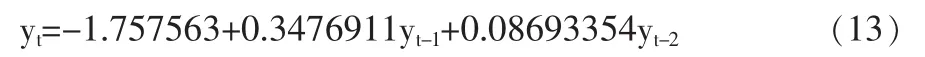
状态转移概率为:
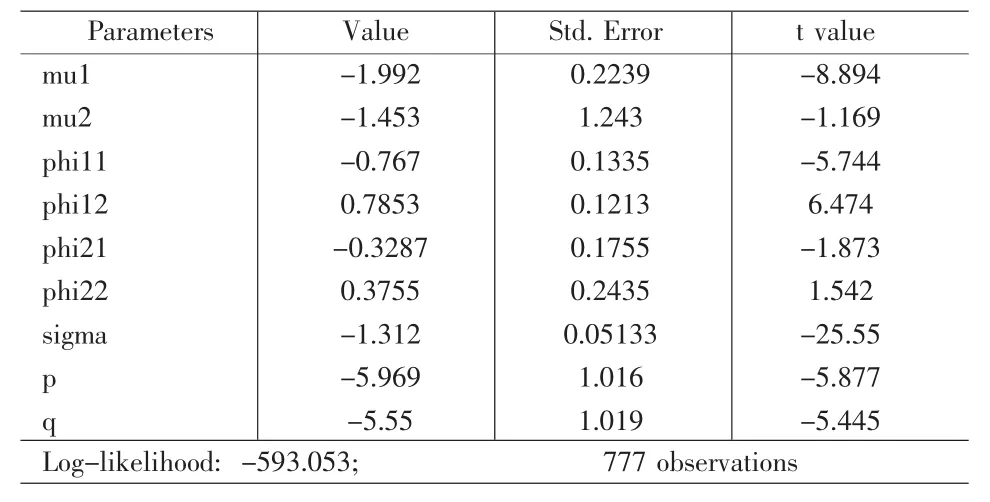
表2 马尔可夫转换模型参数估计

式(12)说明股市在稳定的状态,前两周的波动率与该周的波动率有很好的线性关系,而且两者权重差别不大。式(13)说明股市在不稳定状态下,该周的波动率与前一周的波动率相关,而与前两周的波动率关系很小,这是由于股市在不稳定状态下,新信息对市场冲击要比稳定状态下对市场的冲击大。
式(14)说明股市从稳定状态到稳定状态的概率为99.7%,而从不稳定状态到不稳定状态的概率为99.6%,若该时间序列是平稳的,通过式(14)可得两种状态下无条件概率:

说明状态稳定的无条件概率为0.6,状态不稳定的无条件概率为0.4,证券市场大部分时间还是处于稳定状态下。
3 模型解释
本文目的是对中国证券市场波动性整体变化进行分析,即考察某一时点下市场状态的概率值,也就是对Pr(St=j|γt)进行估计。利用式(9)和实证检验所得的对参数的估计值,可得到全样本估计时状态1(稳定状态)的平滑概率图,表示稳定状态在各个时点的概率大小,如图3。
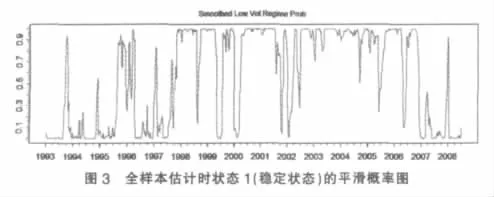
从图3中,可将上海证券市场从1993~2008年分成三个时期。第一个时期从1993~1998年。这个时期是证券市场初创时期市场波动性大。该时期投资者还没有形成成熟的理性投资理念,政策在该时期的影响尤为显著:1994年7月底的“三大政策”救市,1995年停止国债期货交易以及1996年下半年至1997年上半年的一系列政策调控等。虽然这一系列政策目的是在于建立相对稳定的政策调控机制,但由于采取措施的强烈行政性和强制性特点,在中国市场规模相对还不是很大的情况下,结果往往造成了价格暴跌与暴涨,加之该时期没有涨跌停板和T+1交易的限制,更加剧了市场波动性。
第二个时期从1998~2006年中期,这段时期股市比较稳定。1998年6月降低印花税和央行降息两大消息促进了股市的波动,但很快与9月份波动就归于平稳。同样1999年6月央行全面降息也让股市疯狂了3个月。2000年初央行允许券商、基金投资公司进入银行间债券市场以及证监会改革股票发行方式也让股市从稳定状态转变为不稳定状态。之后股市进入缓慢上涨状态,而且波动比较稳定。2001年6月的国有股减持政策的推出,股市反映强烈,之后中石化破发,《证券公司管理办法》、《上市公司治理准则》等出台使的这次波动持续一年之久才归于平静。而且股市对政策的影响的承受应能力也在加强。2005年4月启动的股权分置改革,是这段时期最后一次波动并持续了三个月。
第三个时期从2006年中期至2008年7月。影响这段时间股价波动的因素很多,主要有汇率制度的变动,导致热钱的大量涌入;房地产行业调控,使得资金流入股市;当然最主要还是全民炒股。投资者的“羊群效应”导致了证券市场波动率的放大,引发证券市场大的震荡。虽然在这当中政府曾通过调整印花税,来减少波动性。但在此氛围下,这些政策事件对证券市场影响的信号也理所当然被放大,引起证券市场产生大的波动。而“牛市”中的“利好”政策和“熊市”中的“利空”政策就更容易产生“羊群效应”,因为这种政策信息更符合大多数人的判断。
4 结论
本文利用马尔可夫转换模型对中国股票波动性进行研究。利用上证指数历史数据对模型的参数进行估计,并得到了证券市场波动的状态平滑概率图。研究发现该模型可较好对我国上海证券市场股价波动性进行估计。利用统计结果分析了我国证券市场波动性的成因和特点。该模型不仅可以用来为政策的制定提供依据,而且对金融衍生品的定价也有一定参考意义。
[1]Hamilton J.A New Approach to the Economic Analysis of Nonstationary Time Series and the Business Cycle[J].Econometrica,1989,(57).
[2]Kim C J.Dynamic Linear Models with Markov Switching[J].Journal of Econometrics,1994,(60).
[3]Hamilton J.AnalysisofTimeSeriesSubjecttoChangesin Regime[J].Journal of Econometrics,1990,(45).
[4]许均华,李启亚等.宏观政策对我国股市影响的实证研究[J].经济研究,2001,(9).
[5]彭文平,肖继辉.股市政策与股市波动[J].上海经济研究,2002,(3).
[6]邹昊平,唐利民,袁国良.政策性因素对中国股市的影响:政府与股市投资者的博弈分析[J].世界经济,2000,(11).
[7]赵振全,张宇.中国股票市场波动和宏观经济波动关系的实证分析[J].数量经济技术经济研究,2000,(6).
[8]严武,肖民赞.我国股市收益波动特征及政策因素影响分析[J].当代财经,2005,(12).
[9]唐齐鸣,李春涛.影响上海股市波动的因素分析[J].数量经济技术经济研究,2000,(11).
(责任编辑/浩 天)
F830.91
A
1002-6487(2010)17-0153-03
葛文雷(1947-),男,上海人,教授,研究方向:金融证券、公司财务。
居新华(1970-),男,江苏人,博士研究生,研究方向:公司财务。

