偶数阶中立型时滞微分方程的振动性

林丹玲

（韩山师范学院 数学与信息技术系，广东 潮州 521041）

偶数阶中立型时滞微分方程的振动性

林丹玲

（韩山师范学院 数学与信息技术系，广东 潮州 521041）

研究一类非线性的偶数阶中立型时滞微分方程，得到了该类方程解振动的几个新的判别准则，得到的结果推广了已有文献中的结果.

非线性；中立型；时滞微分方程；振动

近年对中立型时滞微分方程振动性的研究增长很快[1-5]，然而已有文献大多研究一阶或二阶的情况，对高阶研究较少. 本文考虑如下一般形式的非线性偶数阶中立型方程：

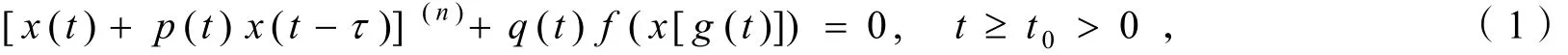
1 引理

引理 1[6]设u∈Cn([t,∞ ),(0,∞))，u(n)(t) ≤0不恒为零，则存在t≥t和整数l∈ {0,1,,n}，n+奇数，使对t≥t有u(k)(t)>0,0≤k≤l且(− 1)k+lu(k)(t) >0,l≤k≤n.

引理2[7]设引理1的条件成立，且u(n−1)(t)u(n)(t)≤0,t≥t，则存在常数θ∈ (0,1)和M>0，使得对充分大的t有

2 主要结果

定理1假设

H2）存在函数H(t,s)∈C′(D,R)及h(t,s)∈C(D,R)，其中D={(t,s)|t≥s≥t0}满足

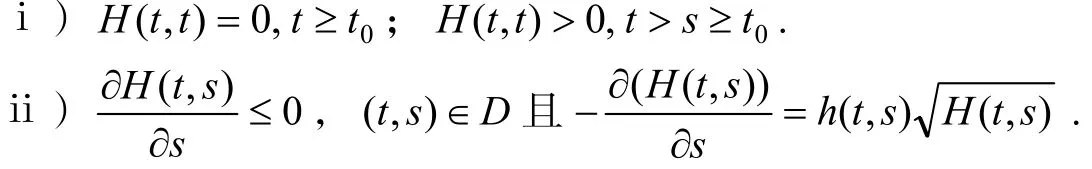
若存在常数θ∈ (0,1)和M>0，使得

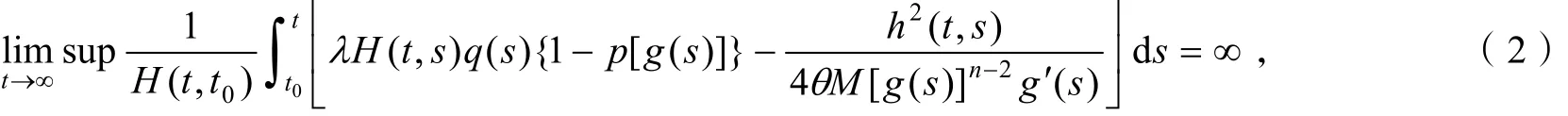
则方程（1）的所有解振动.

证明假设方程（1）有非振动解x(t). 不失一般性，设x(t)是方程（1）的最终正解，则存在t1≥t0使得x(t)> 0,x(t−τ) >0,x[g(t)]>0,t≥t1.

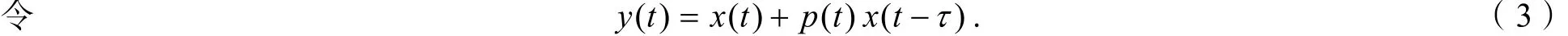
则有y(t)≥x(t)>0,y(n)(t)≤0,t≥t. 由引理1，存在t≥t使得y′(t)>0,y(n−1)(t)>0,t≥t.

1212

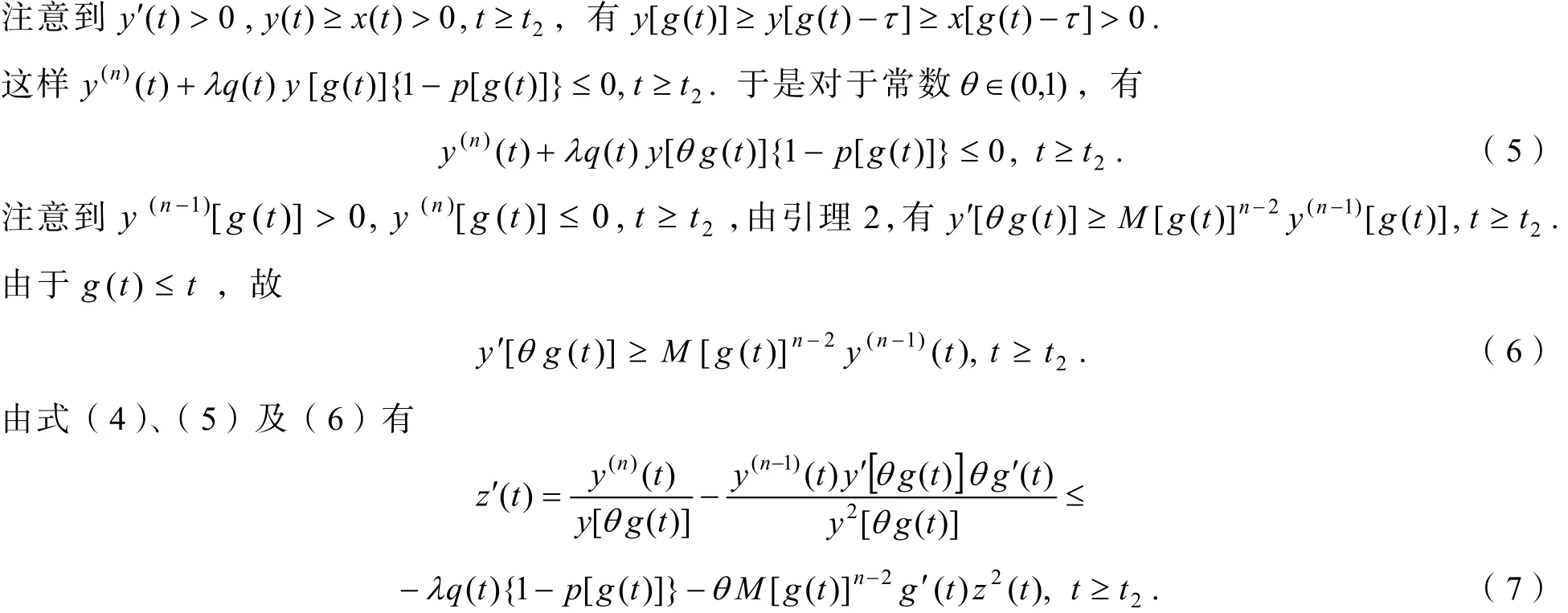
由此可得，对于任意的t≥t2，有

对上式令t→∞，并取上极限得

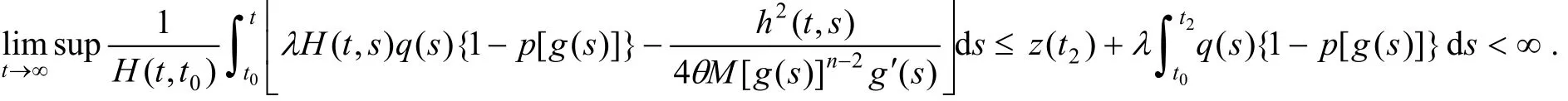
与式（2）矛盾. 证毕.

定理2假设定理1中的条件H1）成立，如果存在常数m≥2和函数ρ(t)∈C′([t0,∞),(0, ∞))，使得

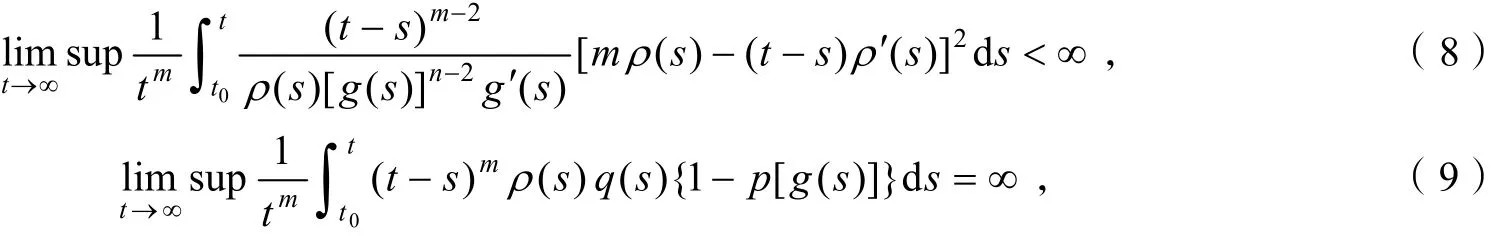
则方程（1）的所有解振动.

证明假设方程（1）有非振动解x(t). 不失一般性，设x(t)是方程（1）的最终正解，则由定理1证明中的式（7），有

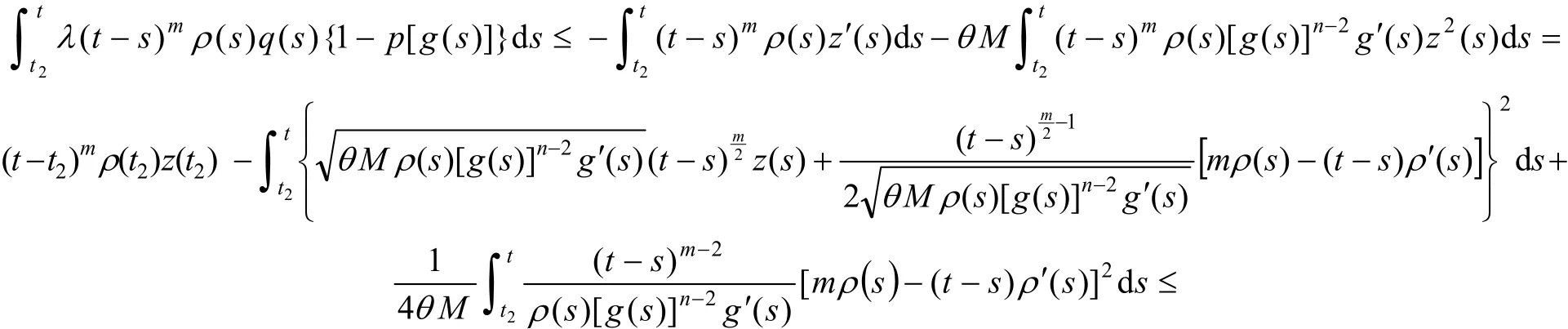
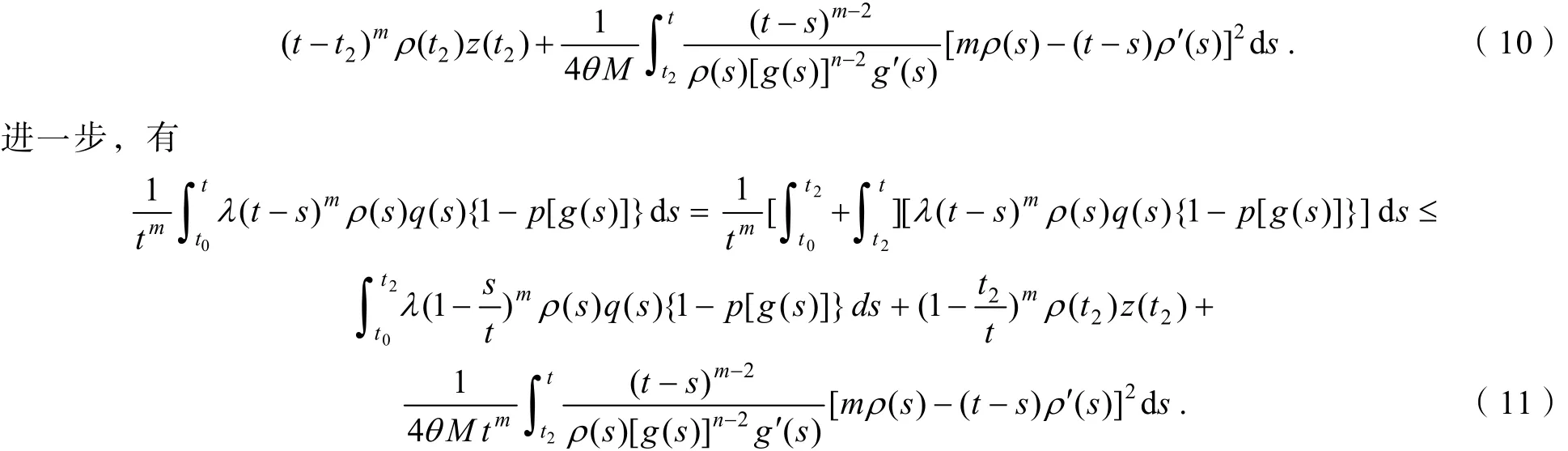
令t→∞，并取上极限得：

则方程（1）的所有解振动.

证明假设方程（1）有非振动解x(t). 不失一般性，设x(t)是方程（1）的最终正解，则由定理2的证明知存在t2≥t1≥t0及常数θ∈ (0,1)和M>0，使得当t>u≥t2时有

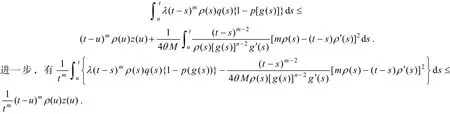
令t→∞，取下极限，并由式（13）可得ϕ(u)≤ρ(u)z(u),u≥t2，因此

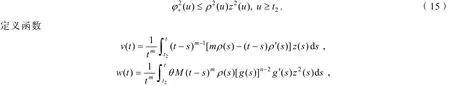
则由式（10）可知

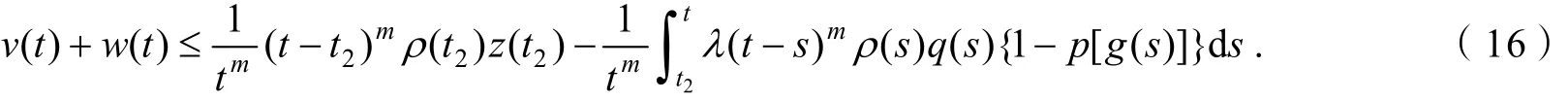
注意到式（13），有

在式（16）中令t→∞，取上极限，并使用式（17）可得

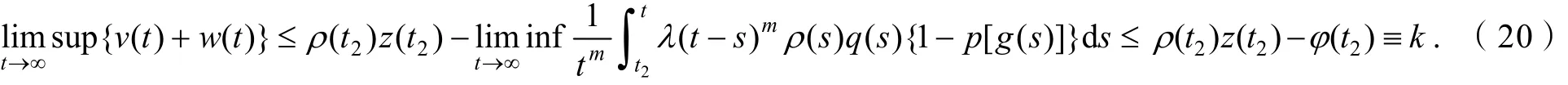
因此对充分大的n，有

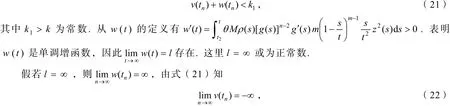
另一方面，由Schwarz不等式得

令n→∞，并注意到式（19），得

与式（14）矛盾. 证毕.

[1]ELABBASY E M, HASSAN T S, SAKER S H. New oscillation criteria for first order nonlinear neutral delay differential equations[J]. J Appl Math Comput, 2006, 2(1/2): 99-118.

[2]ELABBASY E M, HASSAN T S, SAKER S H. Oscillation criteria for first order nonlinear neutral delay differential equations[J]. J Differential Equations, 2005, 134: 1-18.

[3]WANG Peiguang, GE Weigao. Certain of second differential inequality of neutral type [J]. Appl Math Letters, 2000, 13: 45-51.

[4]WANG Peiguang, WU Yonghong. Further results on differential inequality of a class of second order neutral type [J]. Tamkand Journal of Mathematics, 2004, 35(1): 43-51.

[5]师文英，王培光. 一类二阶中立型泛函微分方程的振动性[J]. 数学的实践与认识，2004, 34(3): 125-132.

[6]KIGURADZE I T. On the oscillation of solutions of the equationsgnu=0[J]. Mat Sb, 1964, 65: 172-187.

[7]PHILOS CH G. A new criterion for the oscillatory and asymptotic behavior of delay differential equations [J]. Bull Acad Pol Sci Ser Sci Mat, 1981, 39: 61-64.

[责任编辑：熊玉涛]

Oscillation of Higher Order Neutral Delay Differential Equations

LIN Dan-ling
(Department of Mathematics and Information, Hanshan Teachers College, Chaozhou 521041, China)

The oscillatory criteria of even order nonlinear neutral delay differential equations are studied. The results obtained extend several results in known literature.

nonlinear; neutral; delay differential equation; oscillation

O175

A

1006-7302（2010）02-0006-46

2009-12-10

林丹玲（1963—），女，广东揭阳人，副教授，硕士，研究方向：泛函微分方程，E-mail:cjxldl@126.com.