小波变换及其在地震资料去噪中的应用

赵青峰韩能润郑福荣高 明韩延

(1.西部钻探测井公司 新疆库尔勒) (2.中国石油测井有限公司测井仪器厂 陕西西安)(3.新疆油田公司勘探开发研究院地球物理研究所 新疆库尔勒)

小波变换及其在地震资料去噪中的应用

赵青峰1韩能润1郑福荣2高 明3韩延1

(1.西部钻探测井公司 新疆库尔勒) (2.中国石油测井有限公司测井仪器厂 陕西西安)(3.新疆油田公司勘探开发研究院地球物理研究所 新疆库尔勒)

文章从傅立叶变换不能满足信号处理的要求入手引出小波变换,通过对实际地震资料小波变换去噪前后的效果比较,说明了小波变换是一种分离信号的好方法,能够提高地震资料的分辨率。

地震资料;去噪 ;傅立叶变换;小波变换

0 引 言

长期以来,在地震资料处理中,傅立叶变换是一种常用的工具。但傅立叶变换是在整个时间(或空间)轴的积分,将信号中的突变信息平滑掉了,由傅立叶变换难以确定突变点在时域(或空域)内的位置。

为了能在时域(或空域)和频域内同时分析信号,Gabor引入了加窗傅立叶变换的概念。他用一个在有限区间(称为窗口)外恒等于零的光滑函数去乘所要研究的函数,然后对它作傅立叶变换,这种变换确实能反映函数在窗口内部的频率特征,因而在研究信号的局部性质的问题中起了一定作用。加窗傅立叶变换的优点主要在于,采用窗函数对信号的乘积运算实现开窗和平移,通过窗中心的平移,实现对信号的局部化分析。但由于窗函数具有唯一性,因而窗口的大小和形状亦是唯一的,即加窗傅立叶变换不具有分辨率的可变性,因而,使人们无法根据信号的变化情况调整分辨率;另外,由于窗函数的存在,导致加窗傅立叶变换的非正交性,给实际应用带来困难。对于窗函数本身而言,当窗很大时,分辨率高;而当窗很小时,分辨率降低,且有严重的吉卜斯现象。

因此,要提高分辨率,降低截断效应,就要有足够的窗口来保证,但在实际问题中往往不可能满足。这样,就提出了一个问题,有没有办法使窗口宽度足够小,而又使分辨率足够高呢?为此,提出小波变换。小波变换的基本思想来源于函数的伸缩与平移,它是通过基小波函数的伸缩与平移来构成一系列分辨率不同的正交投影空间及其对应的基,这是小波变换不同于傅氏变换之所在,正因如此,小波变换就不再要求信号是平稳性的,且具有可变的时间和频率分辨率[1、2]。

1 小波变换原理

设Ψ(t)∈L2(R)函数,并且满足条件:

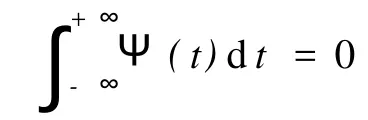
定义:

对于任意函数f(t)∈L2(R)的连续小波变换为:

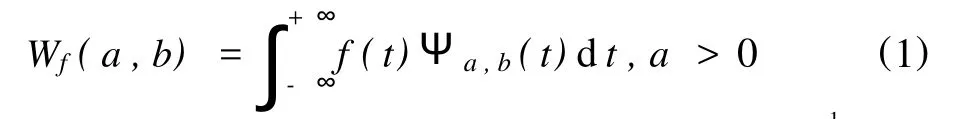
小波变换的基函数Ψa,b(t)(乘因子|a|-12是为了使变换结果归一化而引入的)是窗函数Ψ(t)进行时间平移和尺度伸缩的结果;a的变化可以改变窗口的大小,若尺度参数 a>1,则基函数相当于将窗函数拉伸,使窗口的时宽增大,其频谱变窄并向低频方向移动;而若 a<1则基函数相当于将窗函数压缩,使窗函数缩小,其频谱展宽并向高频方向移动。大的尺度参数对应于低频端,频率分辨率高、时间分辨率低;反之,小的尺度参数对应于高频端,频率分辨率低、时间分辨率高,这就是小波变换的多分辨特性。参数 b起时移作用,b的变化只影响时频窗的中心点在时间轴上的位置,而对时频窗的形状无影响;随着 a的增大,时频窗的中心频率降低,时间宽度增大,但时频窗的面积保持不变,a、b的联合作用可使时频窗覆盖整个相空间。这样,式(1)就相当于用一系列不同宽度的时窗去分析f(t)在 b时刻附近的频率成分,由于Ψ(t)是局域化的,因而小波变换同时具有良好的频域局部性和时域局部性,即可以实现对信号的“变焦”分析[3]。

在实际应用中,需要对尺度参数 a和平移参数b进行离散化,通常取 a=2j,b=k2j,j,k为整数。

2 小波变换去噪的基本原理及方法

由式(1)可以看出,小波变换表现为一系列的褶积运算。对信号进行小波分解,实质上就是对信号用不同的滤波器进行滤波,这些滤波器的脉冲响应就是一系列的小波基。对应于不同尺度参数 a的小波基,将信号分解成不同的频带成分,对分频后的记录进行增益控制。这样可以达到增强有效波、压制干扰波、消除地层对地震波高频成分的吸收,恢复地震记录的理想状态,从而达到提高地震记录分辨率的目的[4、5]。

利用小波变换对地震信号进行去噪的方法是:将每个地震道信号进行小波变换,得到地震信号在不同频率刻度上的时间特性,然后根据采样频率、地层特性以及采集仪器的频率特性等先验知识,灵活地选择滤波器响应,对信号进行滤波。

3 应用实例

图1给出了用不同小波尺度 a进行小波变换去噪的结果,从左至右依次为 a、b、c、d、e、f、g,其中 a为原始地震记录,b、c、d、e、f、g 分别为 a=32、16、8、4、2、1时,小波变换去噪的结果。

从图中可见,小波变换后噪声被有效抑制,记录的质量明显改善。另外,根据不同尺度的分频剖面,可以看到这样一个规律,随着尺度的增大,分解出来的波形频率越来越高,原来不明显的次峰值变为明显的主峰值,原来在地震剖面图上不明显的同相轴逐渐变成两个同相轴。因此,在实际资料去噪中要根据不同的需要选择合适的小波尺度 a。

图1 用不同小波尺度去噪结果的对比

4 结 论

小波变换作为一种新的数学工具被引人地震资料去噪邻域虽然还为时甚短,但由于它们具有同时在时间域和频率域进行局部化分析的特点,已显示出强大的生命力和广泛的应用前景。尤其在精细解释和岩性分析中,必将发挥越来越重要的作用。本文仅是用小波变换进行地震资料去噪的一个尝试,还有许多不完善的地方,有待于进一步提高和发展。由实际地震资料的去噪结果表明,利用小波变换对地震资料进行处理可以提高地震资料的信噪比和分辨率。

[1] 魏明果.实用小波分析[M].北京:北京理工大学出版社,2005

[2] 程正兴.小波分析与应用实例[M].西安:西安交通大学出版社,2006

[3] 马朋善,王继强,刘来祥,等.Morlet小波分频处理在提高地震资料分辨率中的应用[J].石油物探,2007,46(3)

[4] 姜绍辉.小波变换及在提高地震资料信噪比中的应用[D].中国海洋大学硕士学位论文,2005

[5] 郭刚明,时立彩,高生军,等.小波变换在地震资料处理中的应用效果分析[J].石油物探,2003,42(2)

P631.4+43

B

1004-9134(2010)02-073-02

2009-05-14 编辑:高红霞)

赵青峰,男,1977年生,毕业于西安石油学院电子仪器及测量技术专业,现在西部钻探测井公司塔里木分公司,从事测井工作。邮编:841000