制动器试验台控制方法的优化模型＊

张 园,施久良,赵振江

(湖州师范学院理学院,浙江湖州313000)

制动器试验台控制方法的优化模型＊

张 园,施久良,赵振江

(湖州师范学院理学院,浙江湖州313000)

针对制动器实验台控制方法的优化问题进行了讨论.通过扭矩关系将电流的问题转化为角速度的关系.根据能量补偿的方法建立了制动器实验台控制方法的一个优化模型,并进行了定量分析及数值仿真,验证了能量补偿方法的有效性.

制动器实验台;数值仿真;能量补偿;优化问题

MSC 2000:93A 30

0 引言

当今社会,汽车已成为人们不可缺少的交通工具,随着人们在享受汽车给生活带来便捷的同时,与之相伴而生的是汽车的安全问题,特别是汽车的制动控制问题,因此汽车制动性能的良好与否随之成为人们的一个焦点话题.本题正是在这种大背景下,针对文献[1]提出的问题,通过建立数学模型,模拟和分析制动器试验台控制方法.

在文献[1]中提出了如下六个问题:

问题一,设车辆单个前轮的滚动半径为0.286m,制动时承受的载荷为6230N,求等效的转动惯量.

问题二,飞轮组由3个外直径1m、内直径0.2m的环形钢制飞轮组成,厚度分别为0.0392m、0.0784m、0.1568m,钢材密度为7810kg/m3,基础惯量为10kg·m2,问可以组成哪些机械惯量?设电动机能补偿的能量相应的惯量的范围为[-30,30]kg·m2,对于问题一中得到的等效的转动惯量,需要用电动机补偿多大的惯量?

问题三,建立电动机驱动电流依赖于可观测量的数学模型.在问题一和问题二的条件下,假设制动减速度为常数,初始速度为50km/h,制动5.0s后车速为零,计算驱动电流.

问题四,对于与所设计的路试等效的转动惯量为48kg·m2、机械惯量为35kg·m2、主轴初转速为514 r/min、末转速为257 r/min、时间步长为10m s的情况,用某种控制方法试验得到的数据见文献[1],请对该方法执行的结果进行评价.

问题五,按照问题三导出的数学模型,给出根据前一个时间段观测到的瞬时转速与/或瞬时扭矩,设计本时间段电流值的计算机控制方法,并对该方法进行评价.

问题六,问题五给出的控制方法是否有不足之处?如果有,请重新设计一个尽量完善的计算机控制方法,并作出评价.

本文就上述问题提出了一些简单和有效的解决方法.

1 符号说明

G:车辆单个前轮制动时承受的载荷;g:重力加速度取9.8N/kg;R:车辆单个前轮的滚动半径;m:车辆单个前轮的质量;mi:第i个飞轮的实心质量;mi′:第i个飞轮空心部分用同样钢材填上的质量;ρ:钢材料密度;Vi:第i个飞轮的实心体积(飞轮体积与飞轮空心部分的体积之和);Vi′:第i个飞轮空心部分的体积;hi:第i个飞轮的厚度;Ji:第i个飞轮的惯量;J:等效转动惯量(题目有解释);J′:机械惯量(题目有解释);M1:电动机驱动力扭距;M2:制动后制动力产生的扭矩;ω:主轴的角加速度;v0:制动时汽车的初始速度;Δt′:把制动时间离散化为许多小时间段Δt′=10ms=0.01s;tk:整个制动时间离散化后的各个时刻tk=kΔt′(k=0,2,…,467);θ0:主轴的初始转速;θt:主轴的末转速;ωk:理论上主轴tk时刻的瞬时角速度; W′:路试时的制动器制动过程消耗的能量(即理论值);W:实验台上制动器在整个制动过程中消耗的能量(即实际值);Δ:路试时的制动器消耗的能量与实验台上制动器在制动过程中消耗的能量的相对误差(即理论值与实际值之间的相对误差).

2 基本假设

(1)理论上把汽车在制动后达到稳态时看作是匀减速运动,使模型理想化;

(2)假设路试时轮胎与地面的摩擦力无穷大,因此轮胎与地面无滑动,只考虑滚动;

(3)为简化分析,假设车辆整个轮胎及其轴承为一圆盘;

(4)不考虑观测误差、随机误差和连续问题离散化,以及离散问题连续化所产生的误差;

(5)假设角加速度的方向为负方向.

3 模型的建立与求解

3.1 求解问题1[1]

假设车辆整个轮胎及其轴承为一圆盘,根据文献[2]可以知道求转动惯量的公式:

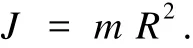
又有:

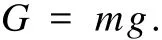
由上两式可以得到:

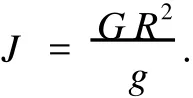
该问已知车辆单个前轮的滚动半径为R=0.286m,制动时承受的载荷G=6230N,故等效的转动惯量J=51.99kg·m2.

3.2 求解问题2[1]

已知飞轮组是由环形钢制飞轮组成的,根据文献[2]得到的求飞轮转动惯量的公式:

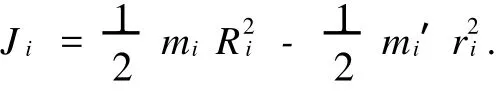
又有:

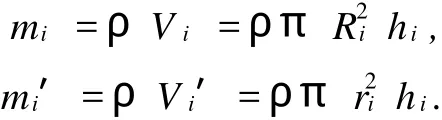
由以上三式得到:

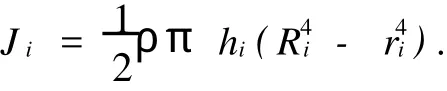
由上式求得三个飞轮的惯量分别为:

已知基础惯量为10kg·m2,根据题意,可以组合成8种不同的机械惯量,其结果见表1.

表1 8种不同机械惯量的组合

求得问题1[1]的等效惯量为J=51.99kg·m2.根据电动机能补偿的能量相应的惯量范围,由表1可得与等效惯量差值最小的机械惯量的组合为J1基础惯量,电动机补偿的惯量为:

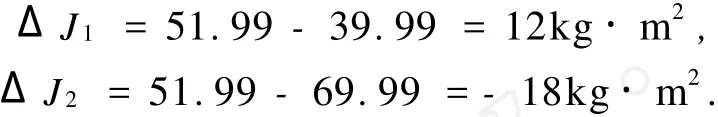
ΔJ1、ΔJ2分别为惯量的反向补偿和正向补偿.

3.3 求解问题3

3.3.1 问题3模型的建立

车辆在制动时,系统的扭矩=驱动力扭矩+制动力扭矩,即刹车的力扭矩.根据文献[1]中等效转动惯量及刚体转动定律[2]可知:制动力扭矩=等效惯量×角加速度.规定ω＊

的方向为负方向有:

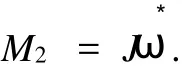
根据假设试验台采用的电动机的驱动电流与其产生的扭矩成正比(本题中比例系数取为K=1.5A/N· m),则设

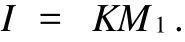
整个系统根据刚体转动定律[2]可以得到公式:

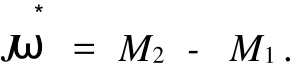
由以上几式,可以推出求电动机驱动电流的模型:

3.3.2 问题3模型的求解

而等效转动惯量为J=51.99kg·m2.根据问题2可知,与该等效惯量的差值最小的机械惯量为:J1′= 39.99kg·m2,J2′=39.99kg·m2.

模型(1)求解,分别求得的电动机驱动电流绝对值为:

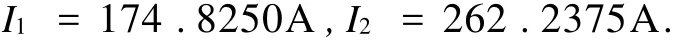
3.4 求解问题4

3.4.1 问题4模型的建立

假设把汽车在制动后达到稳态时看作是匀减速运动,则它在每个时间段其转动的角加速度大小都相等,则有:

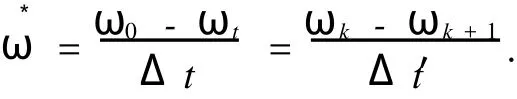
整理后可得:

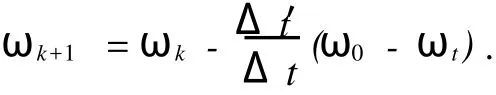
可以看出,上式是一阶差分方程[3],可以通过递推得到ωk公式.具体过程如下:

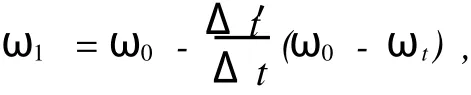
得到求瞬时角速度的模型:

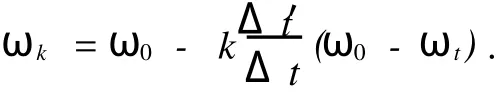
由于问题4给出的是转速,可以把ω0=2πθ0;ωt=2πθt,并且令tk=kΔt′(Δt′=0.01s)代入该式整理得:

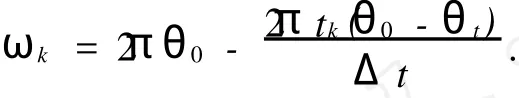
评价控制方法优劣的一个重要数量指标是能量误差的大小,为此,针对问题4求出相对误差Δ=以此评价路试时的制动器与相对应的实验台上制动器在制动过程中消耗能量的大小.

3.4.2 问题4模型的求解

针对文献[1]附录中给出的一些试验数据,利用Matlab编程[4]给出扭矩与时间关系的散点图,以及用曲线拟合的图,见图1.

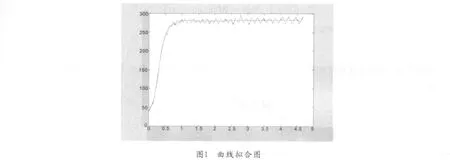
从图1可以看出,达到某个时刻以后,图像的点在某个值附近上下波动,近似于达到了稳定状态,根据图像曲线可以找到tk=1s时,达到稳态,以后的点都是围绕某个值M 附近上下波动,因此对于该方法在一定程度上有其一定的合理性.

下面将分别计算整个过程中理论上能量值与实际产生的能量,并以相对误差来评价该方法的优劣.为此,将时间离散化,从ti-1～ti制动器做的功:

所以总能量:

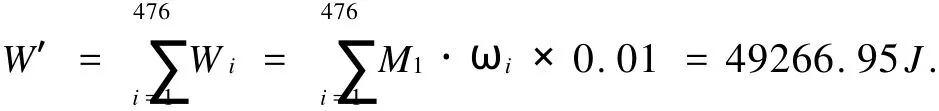
由题设我们可知实际的总能量为:

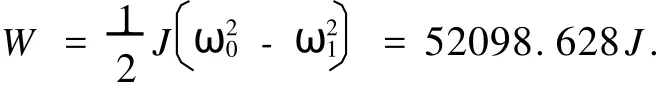
相对误差:

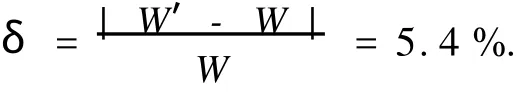
由此可以推断,整个制动过程用路试时的制动器与相对应的实验台上制动器在制动过程中消耗的能量的相对误差较小,该控制方法是可行的.

3.5 问题5模型的建立、求解与评价

假定理想状态为匀减速运动,M1、M2为观测的制动扭矩,T为初始时至停止的时间,wi为理想状态下的角速度,θ1,θ2为转过的初末角,Mi′为电动扭转系数,假设初始表如表2所示:

表2 电动机初始参数

由于假设理想状态即匀减速状态,则

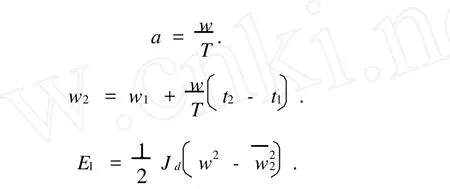
实际中,

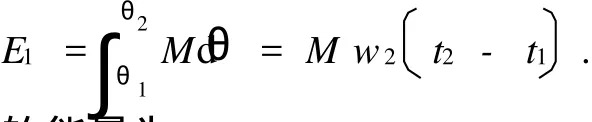
故在[t1,t2]时间段内,电机所需添加的能量为:

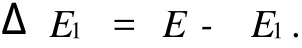
在实际操作中,可通过调整电机扭矩来添加该能量,即令ΔM=kΔE1,其中k为伸缩系数.又

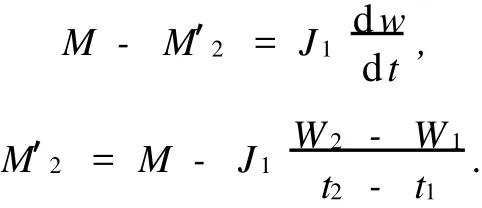
由此可以得到:

在理想状态中,当t=3时,

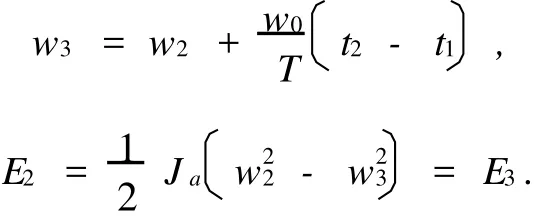
实际状态中:

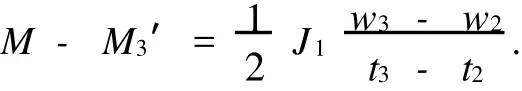
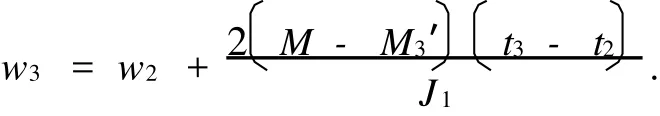
由此可以得到:以此类推,可以算得w4,w5,…,w4,w5,…,从而可以实现理想转速与现实转速差的比较.根据电流和扭矩成正比的关系还可以推算出需要补充的电流.

对于该问,通过电流和扭矩成正比,将瞬时扭矩和电流联系起来,从而将题中研究电流的问题通过将扭矩关系转化为角速度之间的关系进行深入的探讨和研究.在此将模型假定为匀减速来研究,根据能量补偿的方法得到理想模型与所设计模型的定量分析及数值仿真,分析显示出了能量补偿方法的有效性.通过比较可以看出,在匀减速状态中所涉及的方法,从能量的角度与理想的模型是一致的.

3.6 求解问题6

3.6.1 问题6模型的建立与求解

E1′:理论中消耗的能量;E′:制动器消耗的能量;E:电动机消耗的能量;wi:现实的角速度;wi′:理想角速度;a′:理想角加速度;Δw′:理想角速度变量;M0:制动器的扭矩;M1:电动机的扭矩.

本题通过能量守恒定理将理论耗能、制动器耗能及电动机耗能联系起来.通过能量转换,运用理想状态下的能量与现实状态下的能量联系,把电动扭矩联系起来,从而解决问题.

根据能量守恒定理得到:

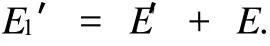
由此得到:

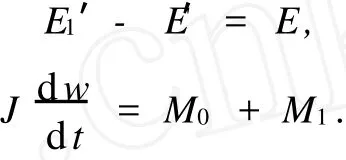
而在理想状态下:

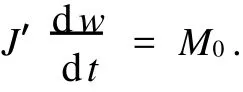
得到:

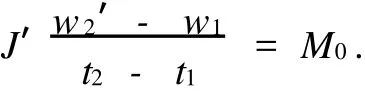
从而

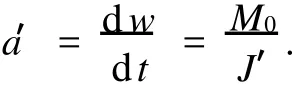
算得M0和理想状态下的a′.也可由此算得在理想状态下的

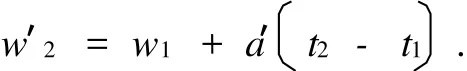
当t1→t2时,另

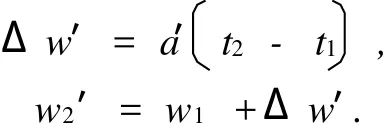
所以由此可以得到理想时制动器的耗能为:

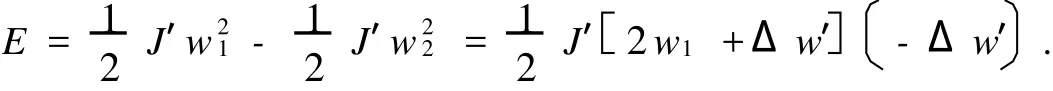
在实验中得到制动器的耗能为:

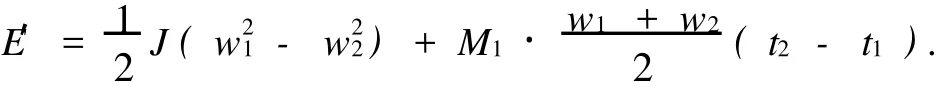
在此,可设一个系数k,使理想扭矩M2′满足:

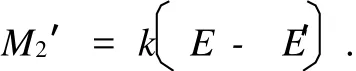
从而

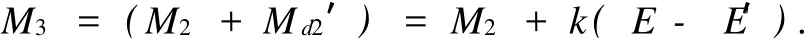
其中,k为可调控的系数.依次类推,我们可以得到后段扭矩和前端扭矩之间的关系,从而进行调控.由M3=M 2+kΔw知当Δw→0时,w控制适当,刚好达到合理的效果.

3.6.2 问题6模型的评价

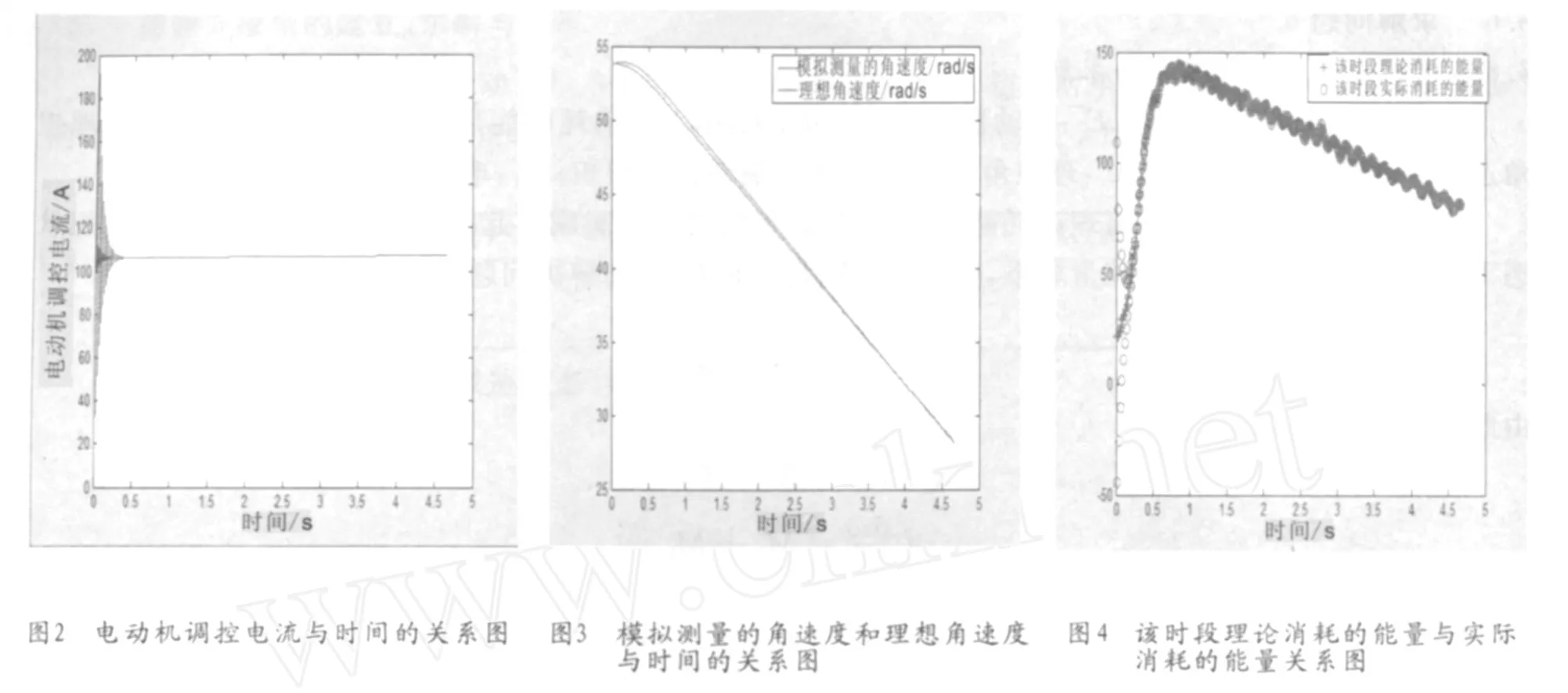
对于问题五最大的不足之处就是将模型过于理想化(理想为做匀减速运动),这可能使误差增大.在改进的过程中首先去除了匀减速运动这个假设,通过引进调控系数k,递推求出一般情况在此优化方案下现实转速,从而使问题更加精确化.从图2、图3、图4中也可以看出模型的效果优势.

通过图2～图4可以观察到在极小的一段时间之后,不管是模拟测量的角速度还是理论消耗的能量与实际的误差都非常小.说明经过改进之后确实大大提高了控制方法的精确性和可行性.

4 模型的评价与推广

利用能量守恒等物理学定律,建立了相应的模型,从而将抽象的理论试验与具体的测量数字之间建立了联系,从而使问题变得可观测、可衡量.

在此建立的控制方法模型可近一步推广到其他领域.比如电机的制作,是典型的能量转化问题,如何将能源运用得最好是数学和物理领域的热门研究话题,而在此通过守恒定律将之与实际联系起来,从而达到与理论最接近,效力最高.本模型不仅可以在物理领域运用,同时可以在生物及制药等领域运用.在生物领域,使能量级间能量流失达到最小,从而获得最大的效益.在制药领域,计算出药量的合理运用,从而达到药效与副作用的最合理程度.总之,运用守恒定律将理论与实际结合起来,在不同领域都有及其广泛的运用.

[1]全国大学生数学建模竞赛组委会.2009高教社杯全国大学生数学建模竞赛A题[EB/OL].2009-09-30.http:// mcm.edu.cn/mcm09/Problem s2009c.asp.

[2]马文薇.物理学教程[M].北京:高等教育出版社,2006:11.

[3]赵静.数学建模与数学实验[M].北京:北京高等教育出版社,2008:159～169.

[4]张瑞丰.精通MA TLAB 6.5[M].北京:中国水利水电出版社,2004:234～309.

Abstract:This paper discusses the op timization p roblem sof the Brake Test Stand Control Methods.The current p roblem s are transformed into the angular velocity p roblem s by the torque relationship.The optimization modelsof the controlmethod for brake test stand were established by using energy compensation method.The quantitative analysis and numerical simulation for gotten op timization models were dow n.And the effect of the energy compensation method was tested and verified.

Key words:brake test stand;numerical simulation;energy compensation;op timization p roblem

MSC 2000:93A 30

The Optim ization M odel of the Control Method for Brake Test Stand

ZHANG Yuan,SH IJiu-liang,ZHAO Zhen-jiang
(Faculty of Science,Houzhou Teachers College,Huzhou 313000,China)

O242.1

A

1009-1734(2010)02-0032-07

2010-03-15

浙江省教育厅科研项目(Y200805528);国家特色专业建设点“数学与应用数学”.

张园,湖州师范学院理学院2007级本科生,从事应用数学研究